|
List Of Games In Game Theory
Game theory studies strategic interaction between individuals in situations called games. Classes of these games have been given names. This is a list of the most commonly studied games Explanation of features Games can have several features, a few of the most common are listed here. *Number of players: Each person who makes a choice in a game or who receives a payoff from the outcome of those choices is a player. *Strategies per player: In a game each player chooses from a set of possible actions, known as pure strategies. If the number is the same for all players, it is listed here. *Number of pure strategy Nash equilibria: A Nash equilibrium is a set of strategies which represents mutual best responses to the other strategies. In other words, if every player is playing their part of a Nash equilibrium, no player has an incentive to unilaterally change their strategy. Considering only situations where players play a single strategy without randomizing (a pure strategy) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
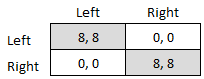
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibrium, Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Effort Game
In game theory, the minimum effort game or weakest link game is a game in which each person decides how much effort to put in and is rewarded based on the least amount of effort anyone puts in. It is assumed that the reward per unit of effort is greater than the cost per unit effort, otherwise there would be no reason to put in effort. Examples * On an island, each person tries to build barriers to protect an island from flooding. Because even a single failed barriers causes the whole island to flood, the flood protection is determined by the weakest barrier. * An airport ground crew must complete all their tasks before an airplane can take off. As a result, the time spent is based on the slowest member of the ground crew. Nash equilibria Source: If there are n players, the set of effort levels is A=\, it costs each player c dollars to put in one unit of effort, and each player is rewarded b dollars for each unit of effort the laziest person puts in, then there are K pure-st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matching Pennies
Matching pennies is a non-cooperative game studied in game theory. It is played between two players, Even and Odd. Each player has a penny and must secretly turn the penny to heads or tails. The players then reveal their choices simultaneously. If the pennies match (both heads or both tails), then Even wins and keeps both pennies. If the pennies do not match (one heads and one tails), then Odd wins and keeps both pennies. Theory Matching Pennies is a zero-sum game because each participant's gain or loss of utility is exactly balanced by the losses or gains of the utility of the other participants. If the participants' total gains are added up and their total losses subtracted, the sum will be zero. The game can be written in a payoff matrix (pictured right - from Even's point of view). Each cell of the matrix shows the two players' payoffs, with Even's payoffs listed first. Matching pennies is used primarily to illustrate the concept of mixed strategies and a mixed str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kuhn Poker
Kuhn poker is a simplified form of poker developed by Harold W. Kuhn as a simple model zero-sum two-player imperfect-information game, amenable to a complete game-theoretic analysis. In Kuhn poker, the deck includes only three playing cards, for example, a King, Queen, and Jack. One card is dealt to each player, which may place bets similarly to a standard poker. If both players bet or both players pass, the player with the higher card wins, otherwise, the betting player wins. Game description In conventional poker terms, a game of Kuhn poker proceeds as follows: *Each player antes 1. *Each player is dealt one of the three cards, and the third is put aside unseen. *Player one can check or bet 1. **If player one checks then player two can check or bet 1. ***If player two checks there is a showdown for the pot of 2 (i.e. the higher card wins 1 from the other player). ***If player two bets then player one can fold or call. ****If player one folds then player two takes the pot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hobbesian Trap
The Hobbesian trap (or Schelling's dilemma) is a theory that explains why preemptive strikes occur between two groups, out of bilateral fear of an imminent attack. Without outside influences, this situation will lead to a fear spiral ( catch-22, vicious circle, Nash equilibrium) in which fear will lead to an arms race which in turn will lead to increasing fear. The Hobbesian trap can be explained in terms of game theory. Although cooperation would be the better outcome for both sides, mutual distrust leads to the adoption of strategies that have negative outcomes for both individual players and all players combined. The theory has been used to explain outbreaks of conflicts and violence, spanning from individuals to states. History An early example of Hobbesian trap reasoning is Thucydides's analysis of the Peloponnesian War in Ancient Greece. Thucydides presented that fear and distrust towards the other side led to an escalation of violence. The theory is most commonly as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guess 2/3 Of The Average
In game theory, "guess of the average" is a game where players simultaneously select a real number between 0 and 100, inclusive. The winner of the game is the player(s) who select a number closest to of the average of numbers chosen by all players. History Alain Ledoux is the founding father of the "guess of the average" game. In 1981, Ledoux used this game as a tie breaker in his French magazine :fr:Jeux et Stratégie, Jeux et Stratégie. He asked about 4,000 readers, who reached the same number of points in previous puzzles, to state an integer between 1 and 1,000,000,000. The winner was the one who guessed closest to of the average guess. Rosemarie Nagel (1995) revealed the potential of guessing games of that kind: They are able to disclose participants' "depth of reasoning." Equilibrium analysis In this game, there is no dominance (game theory), strictly dominant strategy, but there are strongly dominated strategies. There is a unique pure strategy Nash equilibrium. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gift-exchange Game
The gift-exchange game, also commonly known as the gift exchange dilemma, is a common economic game introduced by George Akerlof and Janet Yellen to model reciprocacy in labor relations. The gift-exchange game simulates a labor-management relationship execution problem in the principal-agent problem in labor economics. The simplest form of the game involves two players – an employee and an employer. The employer first decides whether they should award a higher salary to the employee. The employee then decides whether to reciprocate with a higher level of effort (work harder) due to the salary increase or not. Like trust games, gift-exchange games are used to study reciprocity for human subject research in social psychology and economics. If the employer pays extra salary and the employee puts in extra effort, then both players are better off than otherwise. The relationship between an investor and an investee has been investigated as the same type of a game. The gift exchange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Example Of A Game Without A Value
In the mathematical theory of games, in particular the study of zero-sum continuous games, not every game has a minimax value. This is the expected value to one of the players when both play a perfect strategy (which is to choose from a particular PDF). This article gives an example of a zero-sum game that has no value. It is due to Sion and Wolfe. Zero-sum games with a finite number of pure strategies are known to have a minimax value (originally proved by John von Neumann) but this is not necessarily the case if the game has an infinite set of strategies. There follows a simple example of a game with no minimax value. The existence of such zero-sum games is interesting because many of the results of game theory become inapplicable if there is no minimax value. The game Players I and II choose numbers x and y respectively, between 0 and 1. The payoff to player I is K(x,y)= \begin -1 & \text x [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
El Farol Bar Problem
The El Farol bar problem is a problem in game theory. Every Thursday night, a fixed population want to go have fun at the El Farol Bar, unless it's too crowded. * If less than 60% of the population go to the bar, they'll all have more fun than if they stayed home. * If more than 60% of the population go to the bar, they'll all have less fun than if they stayed home. Everyone must decide ''at the same time'' whether to go or not, with no knowledge of others' choices. Paradoxically, if everyone uses a deterministic pure strategy which is symmetric (same strategy for all players), it is guaranteed to fail no matter what it is. If the strategy suggests it will not be crowded, everyone will go, and thus it ''will'' be crowded; but if the strategy suggests it will be crowded, nobody will go, and thus it will ''not'' be crowded, but again no one will have fun. Better success is possible with a probabilistic mixed strategy. For the single-stage El Farol Bar problem, there exists a uniq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dollar Auction
The dollar auction is a non-zero sum sequential game explored by economist Martin Shubik to illustrate how a short-sighted approach to rational choice can lead to decisions that are, in the long-run, irrational. Shubik: 1971. Page 109 Play The setup involves an auctioneer who volunteers to auction off a dollar bill with the following rule: the bill goes to the winner; however, the second-highest bidder also loses the amount that they bid, making them the biggest loser in the auction. The winner can get a dollar for a mere 5 cents (the minimum bid), but only if no one else enters into the bidding war. However, entering the auction with a low bid may result in a problematic outcome. For instance, a player might begin by bidding 5 cents, hoping to make a 95-cent profit. They can be outbid by another player bidding 10 cents, as a 90-cent profit is still desirable. Similarly, another bidder may bid 15 cents, making an 85-cent profit. Meanwhile, the second bidder may attempt to conve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diner's Dilemma
In game theory, the unscrupulous diner's dilemma (or just diner's dilemma) is an ''n''-player prisoner's dilemma. The situation imagined is that several people go out to eat, and before ordering, they agree to split the cost equally between them. Each diner must now choose whether to order the costly or cheap dish. It is presupposed that the costlier dish is better than the cheaper, but not by enough to warrant paying the difference when eating alone. Each diner reasons that, by ordering the costlier dish, the extra cost to their own bill will be small, and thus the better dinner is worth the money. However, all diners having reasoned thus, they each end up paying for the costlier dish, which by assumption, is worse than had they each ordered the cheaper. Formal definition and equilibrium analysis Let ''a'' represent the joy of eating the expensive meal, ''b'' the joy of eating the cheap meal, ''k'' is the cost of the expensive meal, ''l'' the cost of the cheap meal, and ''n'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |