HOME

TheInfoList



Click Here for Items Related To - Cubic honeycomb
OR:
Cubic honeycomb on:   [Wikipedia]   [Google]   [Amazon]

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of
cubic Cubic may refer to: Science and mathematics * Cube (algebra), "cubic" measurement * Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex ** Cubic crystal system, a crystal system w ...
cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with
Schläfli symbol In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
. John Horton Conway called this honeycomb a cubille.


Related honeycombs

It is part of a multidimensional family of hypercube honeycombs, with
Schläfli symbol In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
s of the form , starting with the square tiling, in the plane. It is one of 28 uniform honeycombs using convex uniform polyhedral cells.


Isometries of simple cubic lattices

Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems:


Uniform colorings

There is a large number of uniform colorings, derived from different symmetries. These include:


Projections

The ''cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a triangular tiling. A square symmetry projection forms a square tiling.


Related polytopes and honeycombs

It is related to the regular
4-polytope In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), an ...
tesseract,
Schläfli symbol In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
, which exists in 4-space, and only has ''3'' cubes around each edge. It's also related to the order-5 cubic honeycomb, Schläfli symbol , of hyperbolic space with 5 cubes around each edge. It is in a sequence of polychora and honeycombs with octahedral vertex figures. It in a sequence of regular polytopes and honeycombs with
cubic Cubic may refer to: Science and mathematics * Cube (algebra), "cubic" measurement * Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex ** Cubic crystal system, a crystal system w ...
cells Cell most often refers to: * Cell (biology), the functional basic unit of life Cell may also refer to: Locations * Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
.


Related polytopes

The cubic honeycomb has a lower symmetry as a runcinated cubic honeycomb, with two sizes of
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s. A double symmetry construction can be constructed by placing a small cube into each large cube, resulting in a nonuniform honeycomb with
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s, square prisms, and rectangular trapezoprisms (a cube with ''D2d'' symmetry). Its vertex figure is a triangular pyramid with its lateral faces augmented by tetrahedra.
Dual cell The resulting honeycomb can be alternated to produce another nonuniform honeycomb with regular tetrahedra, two kinds of tetragonal disphenoids, triangular pyramids, and sphenoids. Its vertex figure has ''C3v'' symmetry and has 26 triangular faces, 39 edges, and 15 vertices.


Related Euclidean tessellations

The ,3,4 , Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated cubic honeycomb) is geometrically identical to the cubic honeycomb. The ,31,1 , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb. This honeycomb is one of five distinct uniform honeycombs constructed by the _3 Coxeter group. The symmetry can be multiplied by the symmetry of rings in the
Coxeter–Dynkin diagram In geometry, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing the spatial relations between a collection of mirrors (or reflecting hyperplanes). It describe ...
s: ----


Rectified cubic honeycomb

The rectified cubic honeycomb or rectified cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra and
cuboctahedra A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a t ...
in a ratio of 1:1, with a square prism vertex figure. John Horton Conway calls this honeycomb a cuboctahedrille, and its dual an
oblate octahedrille The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John H ...
.


Projections

The ''rectified cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Symmetry

There are four uniform colorings for the cells of this honeycomb with reflective symmetry, listed by their Coxeter group, and Wythoff construction name, and the Coxeter diagram below. This honeycomb can be divided on trihexagonal tiling planes, using the hexagon centers of the cuboctahedra, creating two triangular cupolae. This scaliform honeycomb is represented by Coxeter diagram , and symbol s3, with
coxeter notation In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram ...
symmetry +,6,3 : .


Related polytopes

A double symmetry construction can be made by placing octahedra on the cuboctahedra, resulting in a nonuniform honeycomb with two kinds of octahedra (regular octahedra and triangular antiprisms). The vertex figure is a
square bifrustum The square bifrustum or ''square truncated bipyramid'' is the second in an infinite series of bifrustum polyhedra. It has 4 trapezoidal and 2 square faces. This polyhedron can be constructed by taking a square bipyramid (octahedron) and truncati ...
. The dual is composed of
elongated square bipyramid In geometry, the elongated square bipyramid (or elongated octahedron) is one of the Johnson solids (). As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves. It has been named ...
s.
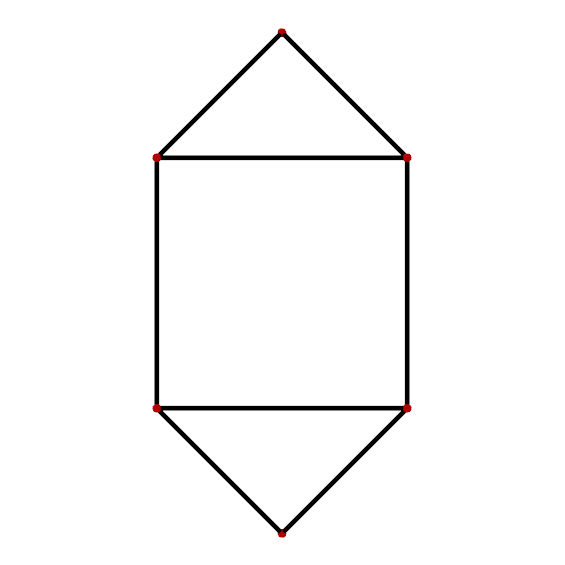Dual cell ----


Truncated cubic honeycomb

The truncated cubic honeycomb or truncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1, with an isosceles
square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid, ...
vertex figure. John Horton Conway calls this honeycomb a truncated cubille, and its dual
pyramidille The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John ...
.


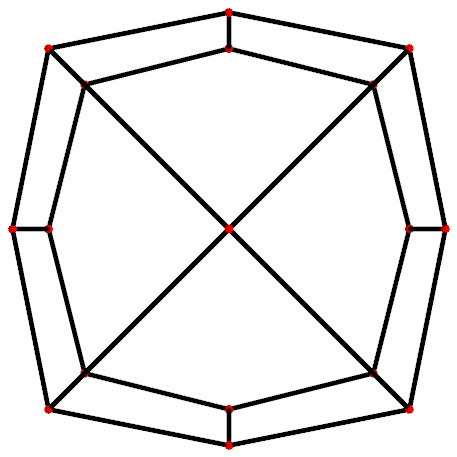
Projections

The ''truncated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Symmetry

There is a second uniform coloring by reflectional symmetry of the Coxeter groups, the second seen with alternately colored truncated cubic cells.


Related polytopes

A double symmetry construction can be made by placing octahedra on the truncated cubes, resulting in a nonuniform honeycomb with two kinds of octahedra (regular octahedra and triangular antiprisms) and two kinds of tetrahedra (tetragonal disphenoids and digonal disphenoids). The vertex figure is an octakis square cupola.
Vertex figure
Dual cell ----


Bitruncated cubic honeycomb

The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
(or, equivalently, bitruncated cubes). It has four
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
around each vertex, in a tetragonal disphenoid vertex figure. Being composed entirely of
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs. John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an ''oblate tetrahedrille'', also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical
disphenoid tetrahedron In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same sh ...
cells with
isosceles triangle In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ...
faces.


Projections

The ''bitruncated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a nonuniform
rhombitrihexagonal tiling In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr. John Conway calls it a rhombihexadeltille.Conway, 2008, ...
. A square symmetry projection forms two overlapping truncated square tiling, which combine together as a
chamfered square tiling In geometry, the chamfered square tiling or semitruncated square tiling is a tiling of the Euclidean plane. It is a square tiling with each edge Chamfer (geometry), chamfered into new hexagonal faces. It can also be seen as the intersection of tw ...
.


Symmetry

The vertex figure for this honeycomb is a
disphenoid tetrahedron In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same sh ...
, and it is also the Goursat tetrahedron (
fundamental domain Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each o ...
) for the _3 Coxeter group. This honeycomb has four uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff constructions. These uniform symmetries can be represented by coloring differently the cells in each construction.


Related polytopes

Nonuniform variants with ,3,4symmetry and two types of truncated octahedra can be doubled by placing the two types of truncated octahedra to produce a nonuniform honeycomb with
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
and hexagonal prisms (as ditrigonal trapezoprisms). Its vertex figure is a ''C2v''-symmetric triangular bipyramid. This honeycomb can then be alternated to produce another nonuniform honeycomb with pyritohedral icosahedra, octahedra (as triangular antiprisms), and tetrahedra (as sphenoids). Its vertex figure has ''C2v'' symmetry and consists of 2
pentagon In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. A pentagon may be simpl ...
s, 4
rectangle In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s, 4
isosceles triangle In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ...
s (divided into two sets of 2), and 4 scalene triangles. ----


Alternated bitruncated cubic honeycomb

The alternated bitruncated cubic honeycomb or bisnub cubic honeycomb is non-uniform, with the highest symmetry construction reflecting an alternation of the uniform bitruncated cubic honeycomb. A lower-symmetry construction involves regular icosahedra paired with golden icosahedra (with 8 equilateral triangles paired with 12 golden triangles). There are three constructions from three related Coxeter diagrams: , , and . These have symmetry ,3+,4 ,(31,1)+and [4/sup>">.html" ;"title="[4">[4/sup>sup>+ respectively. The first and last symmetry can be doubled as 4,3+,4 and [ [4/sup>+. This honeycomb is represented in the boron atoms of the Allotropes of boron#.CE.B1-rhombohedral boron, α-rhombihedral crystal. The centers of the icosahedra are located at the fcc positions of the lattice. ----


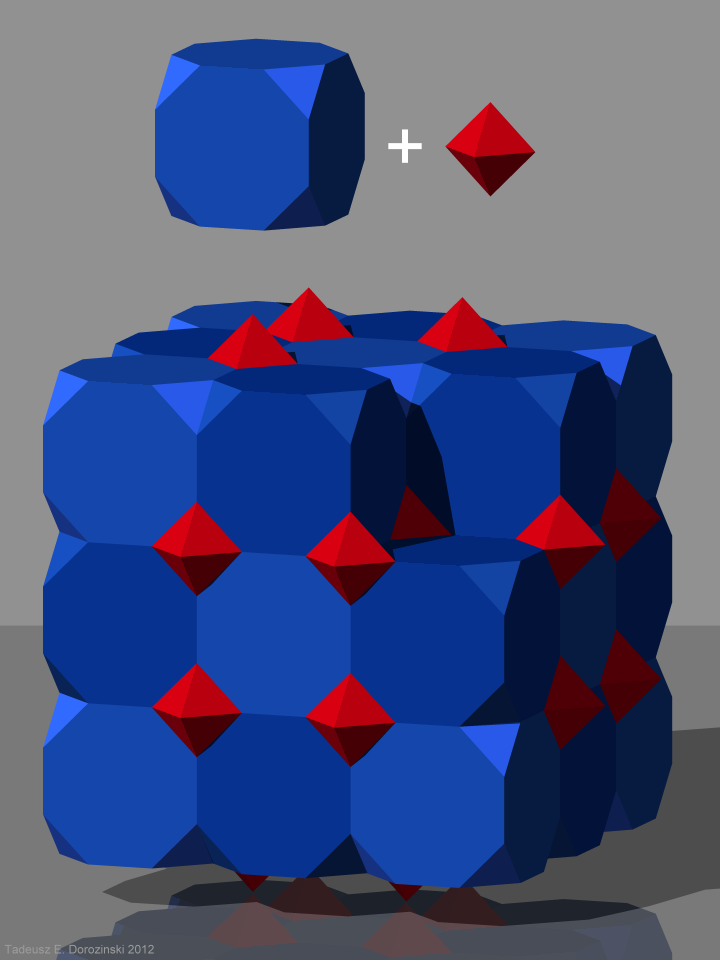
Cantellated cubic honeycomb

The cantellated cubic honeycomb or cantellated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedron, rhombicuboctahedra,
cuboctahedra A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a t ...
, and
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s in a ratio of 1:1:3, with a wedge vertex figure. John Horton Conway calls this honeycomb a 2-RCO-trille, and its dual
quarter oblate octahedrille The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a ...
. :


Images


Projections

The ''cantellated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Symmetry

There is a second uniform colorings by reflectional symmetry of the Coxeter groups, the second seen with alternately colored rhombicuboctahedral cells.


Related polytopes

A double symmetry construction can be made by placing cuboctahedra on the rhombicuboctahedra, which results in the rectified cubic honeycomb, by taking the triangular antiprism gaps as regular octahedra, square antiprism pairs and zero-height tetragonal disphenoids as components of the cuboctahedron. Other variants result in
cuboctahedra A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a t ...
, square antiprisms, octahedra (as triangular antipodiums), and tetrahedra (as tetragonal disphenoids), with a vertex figure topologically equivalent to a
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
with a triangular prism attached to one of its square faces. ----


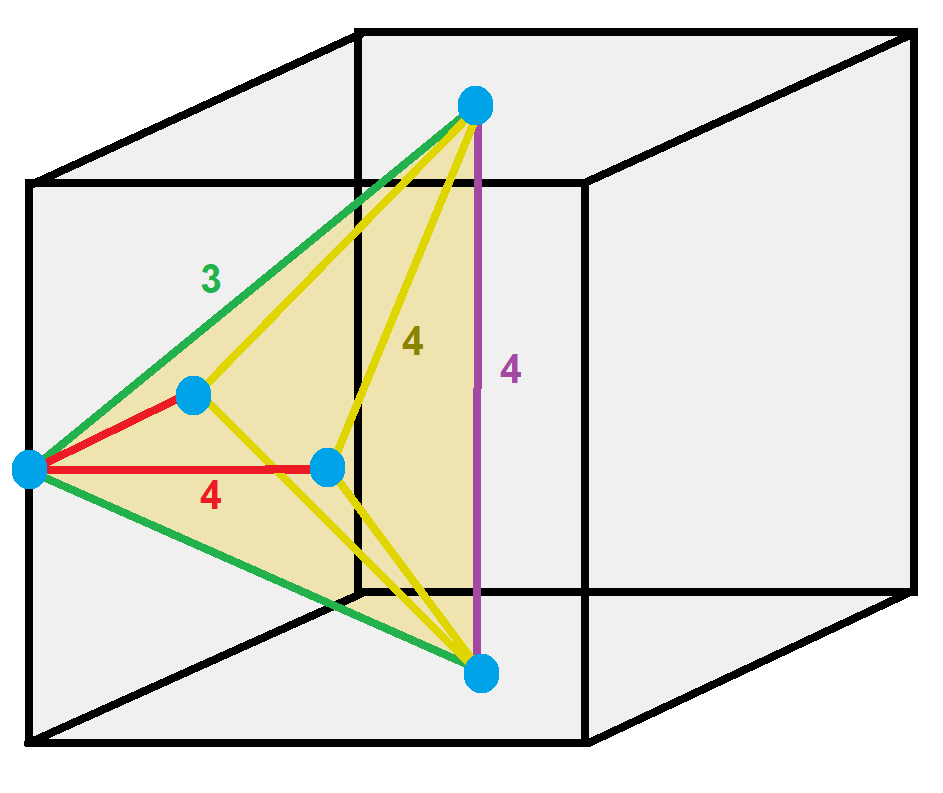
Quarter oblate octahedrille

The dual of the ''cantellated cubic honeycomb'' is called a quarter oblate octahedrille, a catoptric tessellation with Coxeter diagram , containing faces from two of four hyperplanes of the cubic ,3,4fundamental domain. It has irregular triangle bipyramid cells which can be seen as 1/12 of a cube, made from the cube center, 2 face centers, and 2 vertices. :


Cantitruncated cubic honeycomb

The cantitruncated cubic honeycomb or cantitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of truncated cuboctahedra,
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
, and
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s in a ratio of 1:1:3, with a mirrored sphenoid vertex figure. John Horton Conway calls this honeycomb a n-tCO-trille, and its dual
triangular pyramidille The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a re ...
. :  


Images

Four cells exist around each vertex: :


Projections

The ''cantitruncated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Symmetry

Cells can be shown in two different symmetries. The linear Coxeter diagram form can be drawn with one color for each cell type. The bifurcating diagram form can be drawn with two types (colors) of truncated cuboctahedron cells alternating.


Triangular pyramidille

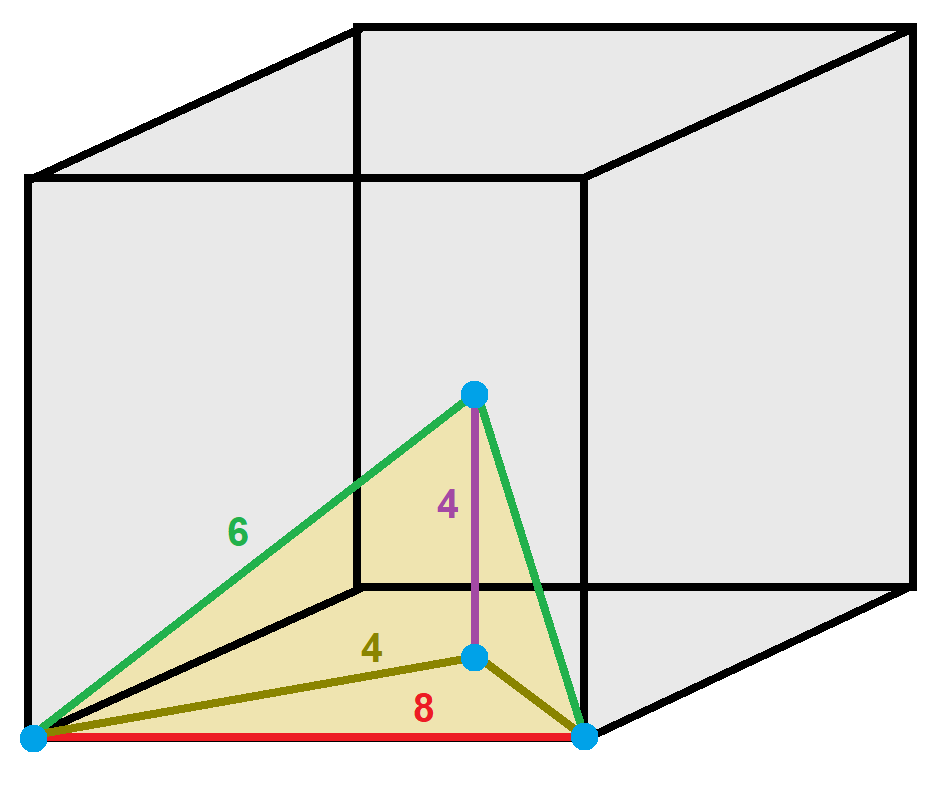
The dual of the ''cantitruncated cubic honeycomb'' is called a triangular pyramidille, with Coxeter diagram, . This honeycomb cells represents the fundamental domains of _3 symmetry. A cell can be as 1/24 of a translational cube with vertices positioned: taking two corner, ne face center, and the cube center. The edge colors and labels specify how many cells exist around the edge. :


Related polyhedra and honeycombs

It is related to a skew apeirohedron with vertex configuration 4.4.6.6, with the octagons and some of the squares removed. It can be seen as constructed by augmenting truncated cuboctahedral cells, or by augmenting alternated truncated octahedra and cubes.


Related polytopes

A double symmetry construction can be made by placing truncated octahedra on the truncated cuboctahedra, resulting in a nonuniform honeycomb with
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
, hexagonal prisms (as ditrigonal trapezoprisms),
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s (as square prisms), triangular prisms (as ''C2v''-symmetric wedges), and tetrahedra (as tetragonal disphenoids). Its vertex figure is topologically equivalent to the octahedron.
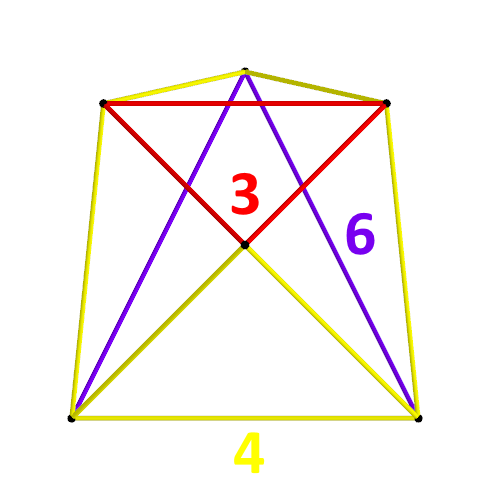
Vertex figure
Dual cell ----


Alternated cantitruncated cubic honeycomb

The alternated cantitruncated cubic honeycomb or snub rectified cubic honeycomb contains three types of cells: snub cubes,
icosahedra In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetri ...
(with ''Th'' symmetry), tetrahedra (as tetragonal disphenoids), and new tetrahedral cells created at the gaps.
Although it is not uniform, constructionally it can be given as Coxeter diagrams or . Despite being non-uniform, there is a near-miss version with two edge lengths shown below, one of which is around 4.3% greater than the other. The snub cubes in this case are uniform, but the rest of the cells are not. ----


Cantic snub cubic honeycomb

The cantic snub cubic honeycomb is constructed by snubbing the
truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
in a way that leaves only
rectangle In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s from the
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s (square prisms). It is not uniform but it can be represented as Coxeter diagram . It has rhombicuboctahedron, rhombicuboctahedra (with ''Th'' symmetry),
icosahedra In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetri ...
(with ''Th'' symmetry), and triangular prisms (as ''C2v''-symmetry wedges) filling the gaps.cantic snub cubic honeycomb
/ref>


Related polytopes

A double symmetry construction can be made by placing icosahedra on the rhombicuboctahedra, resulting in a nonuniform honeycomb with
icosahedra In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetri ...
, octahedra (as triangular antiprisms), triangular prisms (as ''C2v''-symmetric wedges), and
square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid, ...
s.
Vertex figure
Dual cell ----


Runcitruncated cubic honeycomb

The runcitruncated cubic honeycomb or runcitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedron, rhombicuboctahedra, truncated cubes, octagonal prisms, and
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s in a ratio of 1:1:3:3, with an isosceles-trapezoidal pyramid vertex figure. Its name is derived from its Coxeter diagram, with three ringed nodes representing 3 active mirrors in the Wythoff construction from its relation to the regular cubic honeycomb. John Horton Conway calls this honeycomb a 1-RCO-trille, and its dual
square quarter pyramidille The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a ...
.   


Projections

The ''runcitruncated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Related skew apeirohedron

Two related uniform skew apeirohedrons exists with the same vertex arrangement, seen as boundary cells from a subset of cells. One has triangles and squares, and the other triangles, squares, and octagons. :


Square quarter pyramidille

The dual to the ''runcitruncated cubic honeycomb'' is called a square quarter pyramidille, with Coxeter diagram . Faces exist in 3 of 4 hyperplanes of the ,3,4 _3 Coxeter group. Cells are irregular pyramids and can be seen as 1/24 of a cube, using one corner, one mid-edge point, two face centers, and the cube center. :


Related polytopes

A double symmetry construction can be made by placing rhombicuboctahedra on the truncated cubes, resulting in a nonuniform honeycomb with rhombicuboctahedron, rhombicuboctahedra, octahedra (as triangular antiprisms),
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s (as square prisms), two kinds of triangular prisms (both ''C2v''-symmetric wedges), and tetrahedra (as digonal disphenoids). Its vertex figure is topologically equivalent to the augmented triangular prism.
Vertex figure
Dual cell ----


Omnitruncated cubic honeycomb

The omnitruncated cubic honeycomb or omnitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cuboctahedra and octagonal prisms in a ratio of 1:3, with a
phyllic disphenoid In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
vertex figure. John Horton Conway calls this honeycomb a b-tCO-trille, and its dual eighth pyramidille. :  


Projections

The ''omnitruncated cubic honeycomb'' can be orthogonally projected into the euclidean plane with various symmetry arrangements.


Symmetry

Cells can be shown in two different symmetries. The Coxeter diagram form has two colors of truncated cuboctahedra and octagonal prisms. The symmetry can be doubled by relating the first and last branches of the Coxeter diagram, which can be shown with one color for all the truncated cuboctahedral and octagonal prism cells.


Related polyhedra

Two related uniform skew apeirohedron exist with the same vertex arrangement. The first has octagons removed, and vertex configuration 4.4.4.6. It can be seen as truncated cuboctahedra and octagonal prisms augmented together. The second can be seen as augmented octagonal prisms, vertex configuration 4.8.4.8.


Related polytopes

Nonuniform variants with ,3,4symmetry and two types of truncated cuboctahedra can be doubled by placing the two types of truncated cuboctahedra on each other to produce a nonuniform honeycomb with truncated cuboctahedra, octagonal prisms, hexagonal prisms (as ditrigonal trapezoprisms), and two kinds of
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s (as rectangular trapezoprisms and their ''C2v''-symmetric variants). Its vertex figure is an irregular triangular bipyramid.
Vertex figure
Dual cell This honeycomb can then be alternated to produce another nonuniform honeycomb with snub cubes, square antiprisms, octahedra (as triangular antiprisms), and three kinds of tetrahedra (as tetragonal disphenoids, phyllic disphenoids, and irregular tetrahedra).
Vertex figure ----


Alternated omnitruncated cubic honeycomb

An alternated omnitruncated cubic honeycomb or omnisnub cubic honeycomb can be constructed by alternation of the omnitruncated cubic honeycomb, although it can not be made uniform, but it can be given Coxeter diagram: and has symmetry nowiki/>[4,3,4+. It makes snub cubes from the truncated cuboctahedra, square antiprisms from the octagonal prisms, and creates new tetrahedral cells from the gaps.


Dual alternated omnitruncated cubic honeycomb

A dual alternated omnitruncated cubic honeycomb is a space-filling honeycomb constructed as the dual of the alternated omnitruncated cubic honeycomb. 24 cells fit around a vertex, making a chiral octahedral symmetry">#alternated omnitruncated cubic honeycomb">alternated omnitruncated cubic honeycomb. 24 cells fit around a vertex, making a chiral octahedral symmetry that can be stacked in all 3-dimensions: : Individual cells have 2-fold rotational symmetry. In 2D orthogonal projection, this looks like a mirror symmetry. ----


Runcic cantitruncated cubic honeycomb

The runcic cantitruncated cubic honeycomb or runcic cantitruncated cubic cellulation is constructed by removing alternating long rectangles from the octagons and is not uniform, but it can be represented as Coxeter diagram . It has rhombicuboctahedron, rhombicuboctahedra (with ''Th'' symmetry), snub cubes, two kinds of
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s: square prisms and rectangular trapezoprisms (topologically equivalent to a
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
but with ''D2d'' symmetry), and triangular prisms (as ''C2v''-symmetry wedges) filling the gaps. ----


Biorthosnub cubic honeycomb

The biorthosnub cubic honeycomb is constructed by removing alternating long rectangles from the octagons orthogonally and is not uniform, but it can be represented as Coxeter diagram . It has rhombicuboctahedron, rhombicuboctahedra (with ''Th'' symmetry) and two kinds of
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s: square prisms and rectangular trapezoprisms (topologically equivalent to a
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
but with ''D2d'' symmetry). ----


Truncated square prismatic honeycomb

The truncated square prismatic honeycomb or tomo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octagonal prisms and
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s in a ratio of 1:1. It is constructed from a truncated square tiling extruded into prisms. It is one of 28
convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honey ...
s. ----


Snub square prismatic honeycomb

The snub square prismatic honeycomb or simo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s and triangular prisms in a ratio of 1:2. It is constructed from a snub square tiling extruded into prisms. It is one of 28
convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honey ...
s. ----


Snub square antiprismatic honeycomb

A snub square antiprismatic honeycomb can be constructed by alternation of the truncated square prismatic honeycomb, although it can not be made uniform, but it can be given Coxeter diagram: and has symmetry ,4,2,∞sup>+. It makes square antiprisms from the octagonal prisms, tetrahedra (as tetragonal disphenoids) from the
cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...
s, and two tetrahedra from the triangular bipyramids.


See also

* Architectonic and catoptric tessellation * Alternated cubic honeycomb *
List of regular polytopes This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ' ...
* Order-5 cubic honeycomb A hyperbolic cubic honeycomb with 5 cubes per edge * voxel


References

* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) ''The Symmetries of Things'', (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms) * Coxeter, H.S.M. '' Regular Polytopes'', (3rd edition, 1973), Dover edition, p. 296, Table II: Regular honeycombs * George Olshevsky, ''Uniform Panoploid Tetracombs'', Manuscript (2006) ''(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)'' * Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56. * ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380-407, MR 2,10(1.9 Uniform space-fillings) * A. Andreini, ''Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative'' (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129. *
Uniform Honeycombs in 3-Space: 01-Chon
{{Honeycombs Honeycombs (geometry) 4-polytopes Self-dual tilings Regular tessellations