|
Eighth Pyramidille
The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an ''oblate tetrahedrille'' or shortened to ''obtetrahedrille''. Symmetry of Things, Table 21.1. Prime Architectonic and Catopric tilings of space, p. 293, 295. A cell can be seen as 1/12 of a translational cube, with its vertices centered on two faces and two edges. Four of its edges belong to 6 cells, and two edges belong to 4 cells. : The tetrahedral disphenoid honeycomb is the dual of the uniform bitruncated cubic honeycomb. Its vertices form the A / D lattice, which is also known as the body-centered cubic lattice. Geometry This honeycomb's vertex figure is a tetrakis cube: 24 disphenoids meet at each vertex. The union of these 24 disphenoids forms a rhombic dodecahedron. Each edge of the tessellati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or '' close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol . John Horton Conway called this honeycomb a cubille. Related honeycombs It is part of a multidimensional family of hypercube honeycombs, with Schläfli symbols of the form , starting with the square tiling, in the plane. It is one of 28 uniform honeycombs using convex uniform polyhedral cells. Isometries of simple cubic lattices Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems: Uniform colorings There is a large number of uniform colorings, derived from different symmetries. These include: Projections The ''cubic honeycomb'' can be orthogonally projected into the euclidean plane with various s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
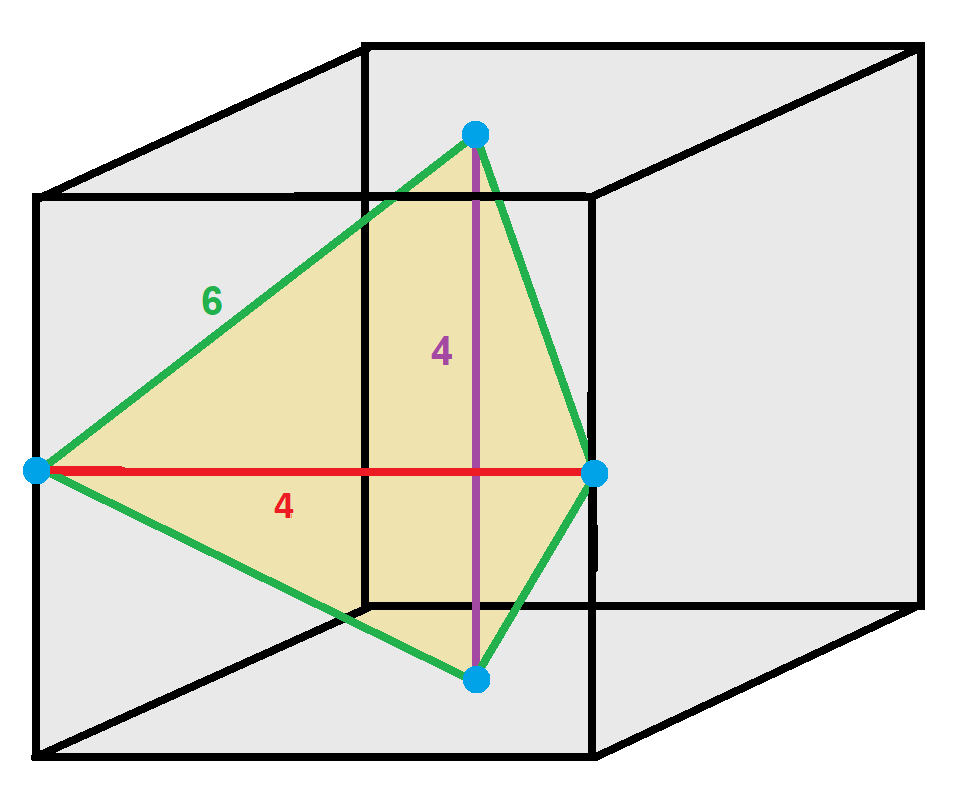
Disphenoid Tetrah Hc
In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,. sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths. Special cases and generalizations If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangles, it is called a tetragonal disphenoid. In t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonal Trapezohedron
In geometry, a trigonal trapezohedron is a rhombohedron (a polyhedron with six rhombus-shaped faces) in which, additionally, all six faces are congruent. Alternative names for the same shape are the ''trigonal deltohedron'' or '' isohedral rhombohedron''. Some sources just call them ''rhombohedra''. Geometry Six identical rhombic faces can construct two configurations of trigonal trapezohedra. The ''acute'' or ''prolate'' form has three acute angle corners of the rhombic faces meeting at the two polar axis vertices. The ''obtuse'' or ''oblate'' or ''flat'' form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices. More strongly than having all faces congruent, the trigonal trapezohedra are isohedral figures, meaning that they have symmetries that take any face to any other face. Special cases A cube can be interpreted as a special case of a trigonal trapezohedron, with square rather than rhombic faces. The two golden rhombohedra are th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term '' rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces ( hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet corres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated Cubic Honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra (or, equivalently, bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs. John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an ''oblate tetrahedrille'', also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces. Geometry It can be realized as the Voronoi tessellation of the body-centred cubic lattice. Lord Kelvin conjectured that a variant of the ''bitruncated cubic honeycomb'' (with curved faces and edges, but th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |