|
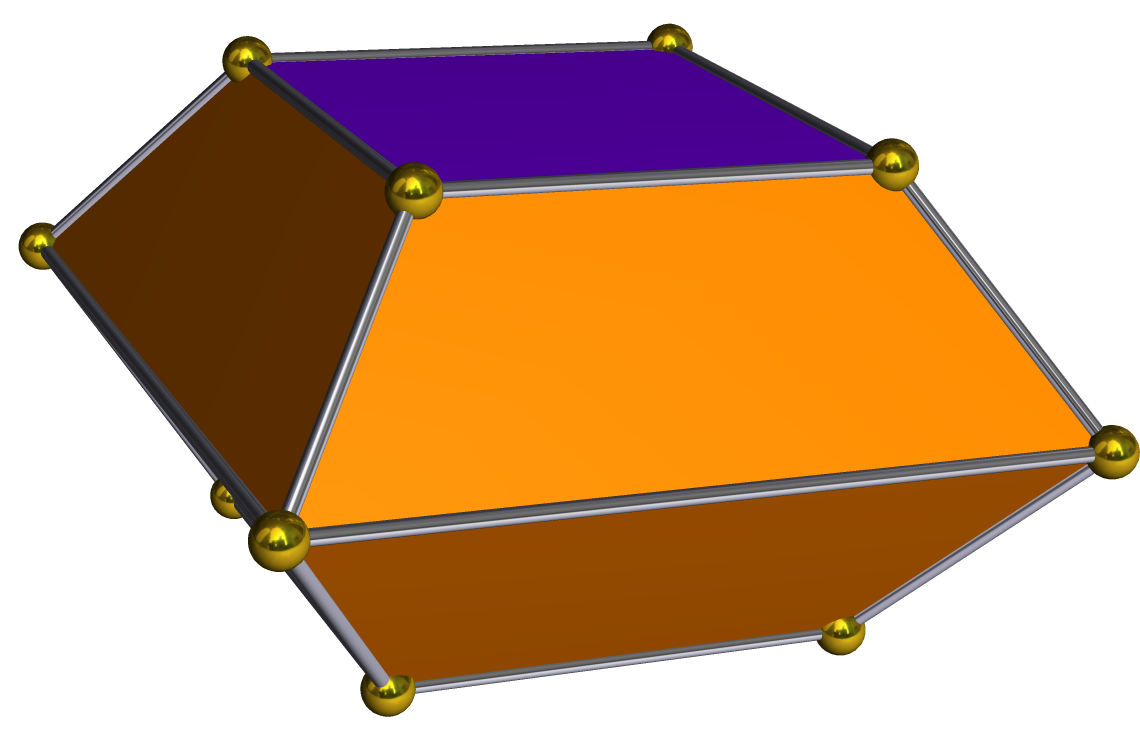
Square Bifrustum
The square bifrustum or ''square truncated bipyramid'' is the second in an infinite series of bifrustum polyhedra. It has 4 trapezoidal and 2 square faces. This polyhedron can be constructed by taking a square bipyramid (octahedron) and truncating the polar axis vertices, making it into two end-to-end frustums. It is dual Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual (grammatical ... to the elongated square dipyramid. Polyhedra {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Elongated Square Dipyramid
Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual (grammatical number), a grammatical category used in some languages * Dual county, a Gaelic games county which in both Gaelic football and hurling * Dual diagnosis, a psychiatric diagnosis of co-occurrence of substance abuse and a mental problem * Dual fertilization, simultaneous application of a P-type and N-type fertilizer * Dual impedance, electrical circuits that are the dual of each other * Dual SIM cellphone supporting use of two SIMs * Aerochute International Dual a two-seat Australian powered parachute design Acronyms and other uses * Dual (brand), a manufacturer of Hifi equipment * DUAL (cognitive architecture), an artificial intelligence design model * DUAL algorithm, or diffusing update algorithm, used to update Internet protocol routing ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifrustum
An ''n''-agonal bifrustum is a polyhedron composed of three parallel planes of ''n''-agons, with the middle plane largest and usually the top and bottom congruent. It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated. They are duals to the family of elongated bipyramids. Formulae For a regular -gonal bifrustum with the equatorial polygon sides , bases sides and semi-height (half the distance between the planes of bases) , the lateral surface area , total area and volume are: :A_l = n (a+b) \sqrt\,, :A = A_l + n \frac\,, :V = n \frach\,. Forms Three bifrusta are duals ''Duals'' is a compilation album by the Irish rock band U2. It was released in April 2011 to u2.com subscribers. Track listing :* "Where the Streets Have No Name" and "Amazing Grace" are studio mix of U2's performance at the Rose Bowl, P ... to three Johnson solids, J14-16. In general, a n-agonal bifru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezoid
A quadrilateral with at least one pair of parallel sides is called a trapezoid () in American and Canadian English. In British and other forms of English, it is called a trapezium (). A trapezoid is necessarily a Convex polygon, convex quadrilateral in Euclidean geometry. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' (or the ''lateral sides'') if they are not parallel; otherwise, the trapezoid is a parallelogram, and there are two pairs of bases). A ''scalene trapezoid'' is a trapezoid with no sides of equal measure, in contrast with the #Special cases, special cases below. Etymology and ''trapezium'' versus ''trapezoid'' Ancient Greek mathematician Euclid defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral with successiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, a funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, a funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice vers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Square Bipyramid
In geometry, the elongated square bipyramid (or elongated octahedron) is one of the Johnson solids (). As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves. It has been named the pencil cube or 12-faced pencil cube due to its shape.Order in Space: A design source book, Keith Critchlow, p.46-47 A zircon crystal is an example of an elongated square bipyramid. Formulae The following formulae for volume (V), surface area (A) and height (H) can be used if all faces are regular, with edge length L: :V = L^3\cdot \left( 1 + \frac\right) \approx L^3\cdot 1.471404521 :A = L^2\cdot \left(4 + 2\sqrt\right) \approx L^2\cdot 7.464101615 :H = L\cdot \left( 1 + \sqrt\right) \approx L\cdot 2.414213562 Dual polyhedron The dual of the elongated square bipyramid is called a square bifrustum and has 10 faces: 8 trapezoidal and 2 square. Related polyhedra and honeycombs A special kind of elongated square bipyramid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipyramid
A (symmetric) -gonal bipyramid or dipyramid is a polyhedron formed by joining an -gonal pyramid and its mirror image base-to-base. An -gonal bipyramid has triangle faces, edges, and vertices. The "-gonal" in the name of a bipyramid does not refer to a face but to the internal polygon base, lying in the mirror plane that connects the two pyramid halves. (If it were a face, then each of its edges would connect three faces instead of two.) "Regular", right bipyramids A ''"regular"'' bipyramid has a ''regular'' polygon base. It is usually implied to be also a ''right'' bipyramid. A ''right'' bipyramid has its two apices ''right'' above and ''right'' below the center or the ''centroid'' of its polygon base. A "regular" right (symmetric) -gonal bipyramid has Schläfli symbol . A right (symmetric) bipyramid has Schläfli symbol , for polygon base . The "regular" right (thus face-transitive) -gonal bipyramid with regular vertices is the dual of the -gonal uniform (thus right) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifrustum
An ''n''-agonal bifrustum is a polyhedron composed of three parallel planes of ''n''-agons, with the middle plane largest and usually the top and bottom congruent. It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated. They are duals to the family of elongated bipyramids. Formulae For a regular -gonal bifrustum with the equatorial polygon sides , bases sides and semi-height (half the distance between the planes of bases) , the lateral surface area , total area and volume are: :A_l = n (a+b) \sqrt\,, :A = A_l + n \frac\,, :V = n \frach\,. Forms Three bifrusta are duals ''Duals'' is a compilation album by the Irish rock band U2. It was released in April 2011 to u2.com subscribers. Track listing :* "Where the Streets Have No Name" and "Amazing Grace" are studio mix of U2's performance at the Rose Bowl, P ... to three Johnson solids, J14-16. In general, a n-agonal bifru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal, the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise it is an oblique frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism (possibly oblique or/and with irregular bases). In computer graphics, the viewing frustum is the three-dimensional region which is visible on the screen. It is formed by a clipped pyramid; in particular, ''frustum culling'' is a method of hidden surface determination. In the aerospace industry, a frustum is the fairing between two stages of a multistage rocket (such as the Saturn V), which is shaped like a truncated cone. Elements, special cases, and related concepts A frustu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |