
In
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the logarithm is the
inverse function to
exponentiation. That means the logarithm of a number to the base is the
exponent
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to re ...
to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in
big O notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Lan ...
.
The logarithm base is called the decimal or
common logarithm
In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered i ...
and is commonly used in science and engineering. The
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
has the number
as its base; its use is widespread in mathematics and
physics, because of its very simple
derivative. The
binary logarithm
In mathematics, the binary logarithm () is the power to which the number must be raised to obtain the value . That is, for any real number ,
:x=\log_2 n \quad\Longleftrightarrow\quad 2^x=n.
For example, the binary logarithm of is , the b ...
uses base and is frequently used in
computer science.
Logarithms were introduced by
John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-accuracy computations more easily. Using
logarithm tables, tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition. This is possible because the logarithm of a
product is the
sum
Sum most commonly means the total of two or more numbers added together; see addition.
Sum can also refer to:
Mathematics
* Sum (category theory), the generic concept of summation in mathematics
* Sum, the result of summation, the additio ...
of the logarithms of the factors:
:
provided that , and are all positive and . The
slide rule, also based on logarithms, allows quick calculations without tables, but at lower precision. The present-day notion of logarithms comes from
Leonhard Euler, who connected them to the
exponential function in the 18th century, and who also introduced the letter as the base of natural logarithms.
Logarithmic scale
A logarithmic scale (or log scale) is a way of displaying numerical data over a very wide range of values in a compact way—typically the largest numbers in the data are hundreds or even thousands of times larger than the smallest numbers. Such a ...
s reduce wide-ranging quantities to smaller scopes. For example, the
decibel
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a po ...
(dB) is a
unit used to express
ratio as logarithms, mostly for signal power and amplitude (of which
sound pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone ...
is a common example). In chemistry,
pH is a logarithmic measure for the
acid
In computer science, ACID ( atomicity, consistency, isolation, durability) is a set of properties of database transactions intended to guarantee data validity despite errors, power failures, and other mishaps. In the context of databases, a sequ ...
ity of an
aqueous solution
An aqueous solution is a solution in which the solvent is water. It is mostly shown in chemical equations by appending (aq) to the relevant chemical formula. For example, a solution of table salt, or sodium chloride (NaCl), in water would be re ...
. Logarithms are commonplace in scientific
formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwee ...
e, and in measurements of the
complexity of algorithms and of geometric objects called
fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
s. They help to describe
frequency ratios of
musical intervals
In music theory, an interval is a difference in pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or ha ...
, appear in formulas counting
prime numbers or
approximating factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
s, inform some models in
psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they produce. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, m ...
, and can aid in
forensic accounting.
The concept of logarithm as the inverse of exponentiation extends to other mathematical structures as well. However, in general settings, the logarithm tends to be a multi-valued function. For example, the
complex logarithm
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in ...
is the multi-valued
inverse
Inverse or invert may refer to:
Science and mathematics
* Inverse (logic), a type of conditional sentence which is an immediate inference made from another conditional sentence
* Additive inverse (negation), the inverse of a number that, when ad ...
of the complex exponential function. Similarly, the
discrete logarithm
In mathematics, for given real numbers ''a'' and ''b'', the logarithm log''b'' ''a'' is a number ''x'' such that . Analogously, in any group ''G'', powers ''b'k'' can be defined for all integers ''k'', and the discrete logarithm log''b' ...
is the multi-valued inverse of the exponential function in finite groups; it has uses in
public-key cryptography.
Motivation

Addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
,
multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
, and
exponentiation are three of the most fundamental arithmetic operations. The inverse of addition is subtraction, and the inverse of multiplication is
division. Similarly, a logarithm is the inverse operation of
exponentiation. Exponentiation is when a number , the ''base'', is raised to a certain power , the ''exponent'', to give a value ; this is denoted
:
For example, raising to the power of gives :
The logarithm of base is the inverse operation, that provides the output from the input . That is,
is equivalent to
if is a positive
real number. (If is not a positive real number, both exponentiation and logarithm can be defined but may take several values, which makes definitions much more complicated.)
One of the main historical motivations of introducing logarithms is the formula
:
which allowed (before the invention of computers) reducing computation of multiplications and divisions to additions, subtractions and
logarithm table looking.
Definition
Given a positive
real number such that , the ''logarithm'' of a positive real number with respect to base is the exponent by which must be raised to yield . In other words, the logarithm of to base is the unique real number such that
.
The logarithm is denoted "" (pronounced as "the logarithm of to base ", "the logarithm of ", or most commonly "the log, base , of ").
An equivalent and more succinct definition is that the function is the
inverse function to the function
.
Examples
* , since .
* Logarithms can also be negative:
since
* is approximately 2.176, which lies between 2 and 3, just as 150 lies between and .
* For any base , and , since and , respectively.
Logarithmic identities
Several important formulas, sometimes called ''logarithmic identities'' or ''logarithmic laws'', relate logarithms to one another.
Product, quotient, power, and root
The logarithm of a product is the sum of the logarithms of the numbers being multiplied; the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of the -th power of a number is '' ''times the logarithm of the number itself; the logarithm of a -th root is the logarithm of the number divided by . The following table lists these identities with examples. Each of the identities can be derived after substitution of the logarithm definitions
or
in the left hand sides.
Change of base
The logarithm can be computed from the logarithms of and with respect to an arbitrary base using the following formula:
:
Starting from the defining identity
:
we can apply to both sides of this equation, to get
:
.
Solving for
yields:
:
,
showing the conversion factor from given
-values to their corresponding
-values to be
Typical
scientific calculators calculate the logarithms to bases 10 and . Logarithms with respect to any base can be determined using either of these two logarithms by the previous formula:
:
Given a number and its logarithm to an unknown base , the base is given by:
:
which can be seen from taking the defining equation
to the power of
Particular bases

Among all choices for the base, three are particularly common. These are , (the
irrational mathematical constant ≈ 2.71828), and (the
binary logarithm
In mathematics, the binary logarithm () is the power to which the number must be raised to obtain the value . That is, for any real number ,
:x=\log_2 n \quad\Longleftrightarrow\quad 2^x=n.
For example, the binary logarithm of is , the b ...
). In
mathematical analysis, the logarithm base is widespread because of analytical properties explained below. On the other hand, logarithms are easy to use for manual calculations in the
decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
number system:
:
Thus, is related to the number of
decimal digit
A numerical digit (often shortened to just digit) is a single symbol used alone (such as "2") or in combinations (such as "25"), to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits (Latin ...
s of a positive integer : the number of digits is the smallest
integer strictly bigger than . For example, is approximately 3.15. The next integer is 4, which is the number of digits of 1430. Both the natural logarithm and the logarithm to base two are used in
information theory
Information theory is the scientific study of the quantification (science), quantification, computer data storage, storage, and telecommunication, communication of information. The field was originally established by the works of Harry Nyquist a ...
, corresponding to the use of
nat
Nat or NAT may refer to:
Computing
* Network address translation (NAT), in computer networking
Organizations
* National Actors Theatre, New York City, U.S.
* National AIDS trust, a British charity
* National Archives of Thailand
* National As ...
s or
bits as the fundamental units of information, respectively. Binary logarithms are also used in
computer science, where the
binary system is ubiquitous; in
music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
, where a pitch ratio of two (the
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
) is ubiquitous and the number of
cents between any two pitches is the binary logarithm, times 1200, of their ratio (that is, 100 cents per
equal-temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, whi ...
semitone); and in
photography to measure
exposure values,
light levels,
exposure times,
apertures, and
film speeds in "stops".
The following table lists common notations for logarithms to these bases and the fields where they are used. Many disciplines write instead of , when the intended base can be determined from the context. The notation also occurs. The "ISO notation" column lists designations suggested by the
International Organization for Standardization (
ISO 80000-2). Because the notation has been used for all three bases (or when the base is indeterminate or immaterial), the intended base must often be inferred based on context or discipline. In computer science, usually refers to , and in mathematics usually refers to . In other contexts, often means .
History
The history of logarithms in seventeenth-century Europe is the discovery of a new
function that extended the realm of analysis beyond the scope of algebraic methods. The method of logarithms was publicly propounded by
John Napier in 1614, in a book titled ''
Mirifici Logarithmorum Canonis Descriptio
''Mirifici Logarithmorum Canonis Descriptio'' (Description of the Wonderful Canon of Logarithms, 1614) and ''Mirifici Logarithmorum Canonis Constructio'' (Construction of the Wonderful Canon of Logarithms, 1619) are two books in Latin by John N ...
'' (''Description of the Wonderful Rule of Logarithms''). Prior to Napier's invention, there had been other techniques of similar scopes, such as the
prosthaphaeresis or the use of tables of progressions, extensively developed by
Jost Bürgi
Jost Bürgi (also ''Joost, Jobst''; Latinisation of names, Latinized surname ''Burgius'' or ''Byrgius''; 28 February 1552 – 31 January 1632), active primarily at the courts in Kassel and Prague, was a Swiss clockmaker, a maker of astronomica ...
around 1600.
Napier coined the term for logarithm in Middle Latin, “logarithmus,” derived from the Greek, literally meaning, “ratio-number,” from ''logos'' “proportion, ratio, word” + ''arithmos'' “number”.
The
common logarithm
In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered i ...
of a number is the index of that power of ten which equals the number. Speaking of a number as requiring so many figures is a rough allusion to common logarithm, and was referred to by
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists ...
as the “order of a number”. The first real logarithms were heuristic methods to turn multiplication into addition, thus facilitating rapid computation. Some of these methods used tables derived from trigonometric identities. Such methods are called
prosthaphaeresis.
Invention of the
function now known as the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
began as an attempt to perform a
quadrature of a rectangular
hyperbola by
Grégoire de Saint-Vincent, a Belgian Jesuit residing in Prague. Archimedes had written ''
The Quadrature of the Parabola
''Quadrature of the Parabola'' ( el, Τετραγωνισμὸς παραβολῆς) is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regar ...
'' in the third century BC, but a quadrature for the hyperbola eluded all efforts until Saint-Vincent published his results in 1647. The relation that the logarithm provides between a
geometric progression in its
argument
An argument is a statement or group of statements called premises intended to determine the degree of truth or acceptability of another statement called conclusion. Arguments can be studied from three main perspectives: the logical, the dialectic ...
and an
arithmetic progression of values, prompted
A. A. de Sarasa
Alphonse Antonio de Sarasa was a Jesuit mathematician who contributed to the understanding of logarithms, particularly as areas under a hyperbola.
Alphonse de Sarasa was born in 1618, in Nieuwpoort (Belgium), Nieuwpoort in Flanders. In 1632 he ...
to make the connection of Saint-Vincent's quadrature and the tradition of logarithms in
prosthaphaeresis, leading to the term “hyperbolic logarithm”, a synonym for natural logarithm. Soon the new function was appreciated by
Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of ...
, and
James Gregory. The notation Log y was adopted by
Leibniz in 1675, and the next year he connected it to the
integral
Before Euler developed his modern conception of complex natural logarithms,
Roger Cotes had a nearly equivalent result when he showed in 1714 that
:
.
Logarithm tables, slide rules, and historical applications
By simplifying difficult calculations before calculators and computers became available, logarithms contributed to the advance of science, especially
astronomy. They were critical to advances in
surveying
Surveying or land surveying is the technique, profession, art, and science of determining the terrestrial two-dimensional or three-dimensional positions of points and the distances and angles between them. A land surveying professional is ca ...
,
celestial navigation
Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space (or on the surface of ...
, and other domains.
Pierre-Simon Laplace called logarithms
::"...
admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations."
As the function is the inverse function of , it has been called an antilogarithm. Nowadays, this function is more commonly called an
exponential function.
Log tables
A key tool that enabled the practical use of logarithms was the ''
table of logarithms''. The first such table was compiled by
Henry Briggs in 1617, immediately after Napier's invention but with the innovation of using 10 as the base. Briggs' first table contained the
common logarithm
In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered i ...
s of all integers in the range from 1 to 1000, with a precision of 14 digits. Subsequently, tables with increasing scope were written. These tables listed the values of for any number in a certain range, at a certain precision. Base-10 logarithms were universally used for computation, hence the name common logarithm, since numbers that differ by factors of 10 have logarithms that differ by integers. The common logarithm of can be separated into an
integer part and a
fractional part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. If the latter is defined as the largest integer not greater than , called floor of or \lfloor x\rfloor, its fractional part can ...
, known as the characteristic and
mantissa. Tables of logarithms need only include the mantissa, as the characteristic can be easily determined by counting digits from the decimal point. The characteristic of is one plus the characteristic of , and their mantissas are the same. Thus using a three-digit log table, the logarithm of 3542 is approximated by
:
Greater accuracy can be obtained by
interpolation
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points.
In engineering and science, one often has a n ...
:
:
The value of can be determined by reverse look up in the same table, since the logarithm is a
monotonic function.
Computations
The product and quotient of two positive numbers and ' were routinely calculated as the sum and difference of their logarithms. The product or quotient came from looking up the antilogarithm of the sum or difference, via the same table:
:
and
:
For manual calculations that demand any appreciable precision, performing the lookups of the two logarithms, calculating their sum or difference, and looking up the antilogarithm is much faster than performing the multiplication by earlier methods such as
prosthaphaeresis, which relies on
trigonometric identities.
Calculations of powers and
roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
are reduced to multiplications or divisions and lookups by
:
and
:
Trigonometric calculations were facilitated by tables that contained the common logarithms of
trigonometric functions.
Slide rules
Another critical application was the
slide rule, a pair of logarithmically divided scales used for calculation. The non-sliding logarithmic scale,
Gunter's rule, was invented shortly after Napier's invention.
William Oughtred enhanced it to create the slide rule—a pair of logarithmic scales movable with respect to each other. Numbers are placed on sliding scales at distances proportional to the differences between their logarithms. Sliding the upper scale appropriately amounts to mechanically adding logarithms, as illustrated here:
For example, adding the distance from 1 to 2 on the lower scale to the distance from 1 to 3 on the upper scale yields a product of 6, which is read off at the lower part. The slide rule was an essential calculating tool for engineers and scientists until the 1970s, because it allows, at the expense of precision, much faster computation than techniques based on tables.
Analytic properties
A deeper study of logarithms requires the concept of a ''
function''. A function is a rule that, given one number, produces another number. An example is the function producing the -th power of from any real number , where the base is a fixed number. This function is written as . When is positive and unequal to 1, we show below that is invertible when considered as a function from the reals to the positive reals.
Existence
Let be a positive real number not equal to 1 and let .
It is a standard result in real analysis that any continuous strictly monotonic function is bijective between its domain and range. This fact follows from the
intermediate value theorem
In mathematical analysis, the intermediate value theorem states that if f is a continuous function whose domain contains the interval , then it takes on any given value between f(a) and f(b) at some point within the interval.
This has two import ...
.
[, section III.3] Now, is
strictly increasing
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
(for ), or strictly decreasing (for ),
is continuous, has domain
, and has range
. Therefore, is a bijection from
to
. In other words, for each positive real number , there is exactly one real number such that
.
We let
denote the inverse of . That is, is the unique real number such that
. This function is called the base- ''logarithm function'' or ''logarithmic function'' (or just ''logarithm'').
Characterization by the product formula
The function can also be essentially characterized by the product formula
:
More precisely, the logarithm to any base is the only
increasing function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of orde ...
''f'' from the positive reals to the reals satisfying and
:
Graph of the logarithm function

As discussed above, the function is the inverse to the exponential function
. Therefore, Their
graphs
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
correspond to each other upon exchanging the - and the -coordinates (or upon reflection at the diagonal line ), as shown at the right: a point on the graph of yields a point on the graph of the logarithm and vice versa. As a consequence,
diverges to infinity (gets bigger than any given number) if grows to infinity, provided that is greater than one. In that case, is an
increasing function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of orde ...
. For , tends to minus infinity instead. When approaches zero, goes to minus infinity for (plus infinity for , respectively).
Derivative and antiderivative

Analytic properties of functions pass to their inverses.
Thus, as is a continuous and
differentiable function, so is . Roughly, a continuous function is differentiable if its graph has no sharp "corners". Moreover, as the
derivative of evaluates to by the properties of the
exponential function, the
chain rule implies that the derivative of is given by
:
That is, the
slope of the
tangent touching the graph of the logarithm at the point equals .
The derivative of is ; this implies that is the unique
antiderivative of that has the value 0 for . It is this very simple formula that motivated to qualify as "natural" the natural logarithm; this is also one of the main reasons of the importance of the
constant .
The derivative with a generalized functional argument is
:
The quotient at the right hand side is called the
logarithmic derivative of '. Computing by means of the derivative of is known as
logarithmic differentiation
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the logarithmic derivative of a function ''f'',
:(\ln f)' = \frac \quad \implies \quad f' = f \cdot (\ ...
. The antiderivative of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
is:
:
Related formulas, such as antiderivatives of logarithms to other bases can be derived from this equation using the change of bases.
Integral representation of the natural logarithm

The
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
of can be defined as the
definite integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with di ...
:
:
This definition has the advantage that it does not rely on the exponential function or any trigonometric functions; the definition is in terms of an integral of a simple reciprocal. As an integral, equals the area between the -axis and the graph of the function , ranging from to . This is a consequence of the
fundamental theorem of calculus and the fact that the derivative of is . Product and power logarithm formulas can be derived from this definition. For example, the product formula is deduced as:
:
The equality (1) splits the integral into two parts, while the equality (2) is a change of variable (). In the illustration below, the splitting corresponds to dividing the area into the yellow and blue parts. Rescaling the left hand blue area vertically by the factor and shrinking it by the same factor horizontally does not change its size. Moving it appropriately, the area fits the graph of the function again. Therefore, the left hand blue area, which is the integral of from to is the same as the integral from 1 to . This justifies the equality (2) with a more geometric proof.

The power formula may be derived in a similar way:
:
The second equality uses a change of variables (
integration by substitution), .
The sum over the reciprocals of natural numbers,
:
is called the
harmonic series. It is closely tied to the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
: as tends to
infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
, the difference,
:
converges (i.e. gets arbitrarily close) to a number known as the
Euler–Mascheroni constant . This relation aids in analyzing the performance of algorithms such as
quicksort.
Transcendence of the logarithm
Real numbers that are not
algebraic are called
transcendental
Transcendence, transcendent, or transcendental may refer to:
Mathematics
* Transcendental number, a number that is not the root of any polynomial with rational coefficients
* Algebraic element or transcendental element, an element of a field exten ...
; for example,
and ''
e'' are such numbers, but
is not.
Almost all
In mathematics, the term "almost all" means "all but a negligible amount". More precisely, if X is a set, "almost all elements of X" means "all elements of X but those in a negligible subset of X". The meaning of "negligible" depends on the math ...
real numbers are transcendental. The logarithm is an example of a
transcendental function. The
Gelfond–Schneider theorem asserts that logarithms usually take transcendental, i.e. "difficult" values.
Calculation

Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using
power series or the
arithmetic–geometric mean, or be retrieved from a precalculated
logarithm table that provides a fixed precision.
Newton's method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valu ...
, an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently. Using look-up tables,
CORDIC-like methods can be used to compute logarithms by using only the operations of addition and
bit shifts. Moreover, the
binary logarithm algorithm calculates
recursively, based on repeated squarings of , taking advantage of the relation
:
Power series
Taylor series
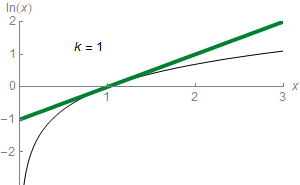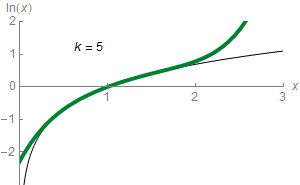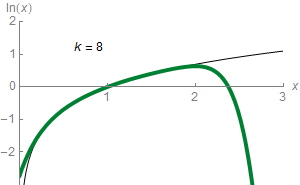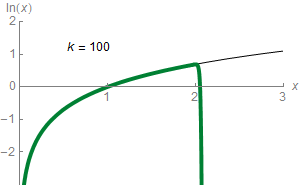
For any real number that satisfies , the following formula holds:
:
This is a shorthand for saying that can be approximated to a more and more accurate value by the following expressions:
:
For example, with the third approximation yields 0.4167, which is about 0.011 greater than . This
series approximates with arbitrary precision, provided the number of summands is large enough. In elementary calculus, is therefore the
limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
of this series. It is the
Taylor series of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
at . The Taylor series of provides a particularly useful approximation to when is small, , since then
:
For example, with the first-order approximation gives , which is less than 5% off the correct value 0.0953.
Although the sequence for
only converges for
, a neat trick can fix this.
:
As
for all
, the sequence converges for the same range of .
Inverse hyperbolic tangent
Another series is based on the
inverse hyperbolic tangent
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions.
For a given value of a hyperbolic function, the corresponding inverse hyperbolic function provides the corresponding hyperbolic angle. The s ...
function:
:
for any real number .
Using
sigma notation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matr ...
, this is also written as
:
This series can be derived from the above Taylor series. It converges quicker than the Taylor series, especially if is close to 1. For example, for , the first three terms of the second series approximate with an error of about . The quick convergence for close to 1 can be taken advantage of in the following way: given a low-accuracy approximation and putting
:
the logarithm of is:
:
The better the initial approximation is, the closer is to 1, so its logarithm can be calculated efficiently. can be calculated using the
exponential series, which converges quickly provided is not too large. Calculating the logarithm of larger can be reduced to smaller values of by writing , so that .
A closely related method can be used to compute the logarithm of integers. Putting
in the above series, it follows that:
:
If the logarithm of a large integer is known, then this series yields a fast converging series for , with a
rate of convergence of
.
Arithmetic–geometric mean approximation
The
arithmetic–geometric mean yields high precision approximations of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
. Sasaki and Kanada showed in 1982 that it was particularly fast for precisions between 400 and 1000 decimal places, while Taylor series methods were typically faster when less precision was needed. In their work is approximated to a precision of (or precise bits) by the following formula (due to
Carl Friedrich Gauss):
:
Here denotes the
arithmetic–geometric mean of and . It is obtained by repeatedly calculating the average (
arithmetic mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The colle ...
) and
(
geometric mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the ...
) of and then let those two numbers become the next and . The two numbers quickly converge to a common limit which is the value of . is chosen such that
:
to ensure the required precision. A larger makes the calculation take more steps (the initial and are farther apart so it takes more steps to converge) but gives more precision. The constants and can be calculated with quickly converging series.
Feynman's algorithm
While at
Los Alamos National Laboratory working on the
Manhattan Project,
Richard Feynman developed a bit-processing algorithm, to compute the logarithm, that is similar to long division and was later used in the
Connection Machine. The algorithm uses the fact that every real number is representable as a product of distinct factors of the form . The algorithm sequentially builds that product , starting with and : if , then it changes to . It then increases
by one regardless. The algorithm stops when is large enough to give the desired accuracy. Because is the sum of the terms of the form corresponding to those for which the factor was included in the product , may be computed by simple addition, using a table of for all . Any base may be used for the logarithm table.
Applications

Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of
scale invariance. For example, each chamber of the shell of a
nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a
logarithmic spiral.
Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to
self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.
Logarithmic scale
A logarithmic scale (or log scale) is a way of displaying numerical data over a very wide range of values in a compact way—typically the largest numbers in the data are hundreds or even thousands of times larger than the smallest numbers. Such a ...
s are useful for quantifying the relative change of a value as opposed to its absolute difference. Moreover, because the logarithmic function grows very slowly for large , logarithmic scales are used to compress large-scale scientific data. Logarithms also occur in numerous scientific formulas, such as the
Tsiolkovsky rocket equation, the
Fenske equation, or the
Nernst equation.
Logarithmic scale

Scientific quantities are often expressed as logarithms of other quantities, using a ''logarithmic scale''. For example, the
decibel
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a po ...
is a
unit of measurement associated with
logarithmic-scale quantities
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a unit ...
. It is based on the common logarithm of
ratios—10 times the common logarithm of a
power ratio or 20 times the common logarithm of a
voltage ratio. It is used to quantify the loss of voltage levels in transmitting electrical signals, to describe power levels of sounds in
acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
, and the
absorbance of light in the fields of
spectrometry and
optics. The
signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in deci ...
describing the amount of unwanted
noise in relation to a (meaningful)
signal is also measured in decibels. In a similar vein, the
peak signal-to-noise ratio is commonly used to assess the quality of sound and
image compression
Image compression is a type of data compression applied to digital images, to reduce their cost for storage or transmission. Algorithms may take advantage of visual perception and the statistical properties of image data to provide superior r ...
methods using the logarithm.
The strength of an earthquake is measured by taking the common logarithm of the energy emitted at the quake. This is used in the
moment magnitude scale or the
Richter magnitude scale. For example, a 5.0 earthquake releases 32 times and a 6.0 releases 1000 times the energy of a 4.0.
Apparent magnitude measures the brightness of stars logarithmically. In
chemistry
Chemistry is the science, scientific study of the properties and behavior of matter. It is a natural science that covers the Chemical element, elements that make up matter to the chemical compound, compounds made of atoms, molecules and ions ...
the negative of the decimal logarithm, the decimal , is indicated by the letter p.
For instance,
pH is the decimal cologarithm of the
activity of
hydronium ions (the form
hydrogen ions take in water). The activity of hydronium ions in neutral water is 10
−7 mol·L−1, hence a pH of 7. Vinegar typically has a pH of about 3. The difference of 4 corresponds to a ratio of 10
4 of the activity, that is, vinegar's hydronium ion activity is about .
Semilog
In science and engineering, a semi-log plot/graph or semi-logarithmic plot/graph has one axis on a logarithmic scale, the other on a linear scale. It is useful for data with exponential relationships, where one variable covers a large range of v ...
(log–linear) graphs use the logarithmic scale concept for visualization: one axis, typically the vertical one, is scaled logarithmically. For example, the chart at the right compresses the steep increase from 1 million to 1 trillion to the same space (on the vertical axis) as the increase from 1 to 1 million. In such graphs,
exponential functions of the form appear as straight lines with
slope equal to the logarithm of .
Log-log graphs scale both axes logarithmically, which causes functions of the form to be depicted as straight lines with slope equal to the exponent . This is applied in visualizing and analyzing
power law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a proportional relative change in the other quantity, inde ...
s.
Psychology
Logarithms occur in several laws describing
human perception:
Hick's law proposes a logarithmic relation between the time individuals take to choose an alternative and the number of choices they have.
Fitts's law
Fitts's law (often cited as Fitts' law) is a predictive model of human movement primarily used in human–computer interaction and ergonomics. The law predicts that the time required to rapidly move to a target area is a function of the ratio betw ...
predicts that the time required to rapidly move to a target area is a logarithmic function of the distance to and the size of the target. In
psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they produce. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, m ...
, the
Weber–Fechner law proposes a logarithmic relationship between
stimulus and
sensation such as the actual vs. the perceived weight of an item a person is carrying. (This "law", however, is less realistic than more recent models, such as
Stevens's power law.)
Psychological studies found that individuals with little mathematics education tend to estimate quantities logarithmically, that is, they position a number on an unmarked line according to its logarithm, so that 10 is positioned as close to 100 as 100 is to 1000. Increasing education shifts this to a linear estimate (positioning 1000 10 times as far away) in some circumstances, while logarithms are used when the numbers to be plotted are difficult to plot linearly.
Probability theory and statistics

Logarithms arise in
probability theory: the
law of large numbers
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials shou ...
dictates that, for a
fair coin, as the number of coin-tosses increases to infinity, the observed proportion of heads
approaches one-half. The fluctuations of this proportion about one-half are described by the
law of the iterated logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Ya. Khinchin (1924). Another statement was given by A ...
.
Logarithms also occur in
log-normal distributions. When the logarithm of a
random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the po ...
has a
normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
, the variable is said to have a log-normal distribution. Log-normal distributions are encountered in many fields, wherever a variable is formed as the product of many independent positive random variables, for example in the study of turbulence.
Logarithms are used for maximum-likelihood estimation of parametric statistical models. For such a model, the likelihood function depends on at least one parametric model, parameter that must be estimated. A maximum of the likelihood function occurs at the same parameter-value as a maximum of the logarithm of the likelihood (the "''log likelihood''"), because the logarithm is an increasing function. The log-likelihood is easier to maximize, especially for the multiplied likelihoods for independence (probability), independent random variables.
Benford's law describes the occurrence of digits in many data sets, such as heights of buildings. According to Benford's law, the probability that the first decimal-digit of an item in the data sample is (from 1 to 9) equals , ''regardless'' of the unit of measurement. Thus, about 30% of the data can be expected to have 1 as first digit, 18% start with 2, etc. Auditors examine deviations from Benford's law to detect fraudulent accounting.
The logarithm transformation is a type of data transformation (statistics), data transformation used to bring the empirical distribution closer to the assumed one.
Computational complexity
Analysis of algorithms is a branch of
computer science that studies the time complexity, performance of algorithms (computer programs solving a certain problem).
[, pp. 1–2] Logarithms are valuable for describing algorithms that Divide and conquer algorithm, divide a problem into smaller ones, and join the solutions of the subproblems.
For example, to find a number in a sorted list, the binary search algorithm checks the middle entry and proceeds with the half before or after the middle entry if the number is still not found. This algorithm requires, on average, comparisons, where is the list's length. Similarly, the merge sort algorithm sorts an unsorted list by dividing the list into halves and sorting these first before merging the results. Merge sort algorithms typically require a time big O notation, approximately proportional to . The base of the logarithm is not specified here, because the result only changes by a constant factor when another base is used. A constant factor is usually disregarded in the analysis of algorithms under the standard uniform cost model.
A function is said to Logarithmic growth, grow logarithmically if is (exactly or approximately) proportional to the logarithm of . (Biological descriptions of organism growth, however, use this term for an exponential function.) For example, any natural number can be represented in Binary numeral system, binary form in no more than
bits. In other words, the amount of memory (computing), memory needed to store grows logarithmically with .
Entropy and chaos

Entropy is broadly a measure of the disorder of some system. In statistical thermodynamics, the entropy ''S'' of some physical system is defined as
:
The sum is over all possible states of the system in question, such as the positions of gas particles in a container. Moreover, is the probability that the state is attained and is the Boltzmann constant. Similarly, entropy (information theory), entropy in information theory measures the quantity of information. If a message recipient may expect any one of possible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified as bits.
Lyapunov exponents use logarithms to gauge the degree of chaoticity of a dynamical system. For example, for a particle moving on an oval billiard table, even small changes of the initial conditions result in very different paths of the particle. Such systems are chaos theory, chaotic in a Deterministic system, deterministic way, because small measurement errors of the initial state predictably lead to largely different final states. At least one Lyapunov exponent of a deterministically chaotic system is positive.
Fractals

Logarithms occur in definitions of the fractal dimension, dimension of
fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
s. Fractals are geometric objects that are self-similar in the sense that small parts reproduce, at least roughly, the entire global structure. The Sierpinski triangle (pictured) can be covered by three copies of itself, each having sides half the original length. This makes the Hausdorff dimension of this structure . Another logarithm-based notion of dimension is obtained by box-counting dimension, counting the number of boxes needed to cover the fractal in question.
Music
Logarithms are related to musical tones and interval (music), intervals. In equal temperament, the frequency ratio depends only on the interval between two tones, not on the specific frequency, or pitch (music), pitch, of the individual tones. For example, the a (musical note), note ''A'' has a frequency of 440 Hertz, Hz and B♭ (musical note), ''B-flat'' has a frequency of 466 Hz. The interval between ''A'' and ''B-flat'' is a
semitone, as is the one between ''B-flat'' and b (musical note), ''B'' (frequency 493 Hz). Accordingly, the frequency ratios agree:
:
Therefore, logarithms can be used to describe the intervals: an interval is measured in semitones by taking the logarithm of the
frequency ratio, while the logarithm of the frequency ratio expresses the interval in
cents, hundredths of a semitone. The latter is used for finer encoding, as it is needed for non-equal temperaments.
Number theory
Natural logarithms are closely linked to prime-counting function, counting prime numbers (2, 3, 5, 7, 11, ...), an important topic in number theory. For any
integer , the quantity of
prime numbers less than or equal to is denoted . The prime number theorem asserts that is approximately given by
:
in the sense that the ratio of and that fraction approaches 1 when tends to infinity. As a consequence, the probability that a randomly chosen number between 1 and is prime is inversely proportionality (mathematics), proportional to the number of decimal digits of . A far better estimate of is given by the logarithmic integral function, offset logarithmic integral function , defined by
:
The Riemann hypothesis, one of the oldest open mathematical conjectures, can be stated in terms of comparing and . The Erdős–Kac theorem describing the number of distinct prime factors also involves the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
.
The logarithm of ''n''
factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
, , is given by
:
This can be used to obtain Stirling's formula, an approximation of for large .
Generalizations
Complex logarithm

All the complex numbers that solve the equation
:
are called ''complex logarithms'' of , when is (considered as) a complex number. A complex number is commonly represented as , where and are real numbers and is an imaginary unit, the square of which is −1. Such a number can be visualized by a point in the complex plane, as shown at the right. The polar form encodes a non-zero complex number by its absolute value, that is, the (positive, real) distance to the origin (mathematics), origin, and an angle between the real () axis'' '' and the line passing through both the origin and . This angle is called the Argument (complex analysis), argument of .
The absolute value of is given by
:
Using the geometrical interpretation of sine and cosine and their periodicity in , any complex number may be denoted as
:
for any integer number . Evidently the argument of is not uniquely specified: both and are valid arguments of for all integers , because adding radian, radians or ''k''⋅360° to corresponds to "winding" around the origin counter-clock-wise by Turn (geometry), turns. The resulting complex number is always , as illustrated at the right for . One may select exactly one of the possible arguments of as the so-called ''principal argument'', denoted , with a capital , by requiring to belong to one, conveniently selected turn, e.g. or . These regions, where the argument of is uniquely determined are called principal branch, ''branches'' of the argument function.

Euler's formula connects the trigonometric functions sine and cosine to the complex exponential:
:
Using this formula, and again the periodicity, the following identities hold:
:
where is the unique real natural logarithm, denote the complex logarithms of , and is an arbitrary integer. Therefore, the complex logarithms of , which are all those complex values for which the power of equals , are the infinitely many values
:
for arbitrary integers .
Taking such that is within the defined interval for the principal arguments, then is called the ''principal value'' of the logarithm, denoted , again with a capital . The principal argument of any positive real number is 0; hence is a real number and equals the real (natural) logarithm. However, the above formulas for logarithms of products and powers Exponentiation#Failure of power and logarithm identities, do ''not'' generalize to the principal value of the complex logarithm.
The illustration at the right depicts , confining the arguments of to the interval . This way the corresponding branch of the complex logarithm has discontinuities all along the negative real axis, which can be seen in the jump in the hue there. This discontinuity arises from jumping to the other boundary in the same branch, when crossing a boundary, i.e. not changing to the corresponding -value of the continuously neighboring branch. Such a locus is called a branch cut. Dropping the range restrictions on the argument makes the relations "argument of ", and consequently the "logarithm of ", multi-valued functions.
Inverses of other exponential functions
Exponentiation occurs in many areas of mathematics and its inverse function is often referred to as the logarithm. For example, the logarithm of a matrix is the (multi-valued) inverse function of the matrix exponential. Another example is the p-adic logarithm function, ''p''-adic logarithm, the inverse function of the p-adic exponential function, ''p''-adic exponential. Both are defined via Taylor series analogous to the real case. In the context of differential geometry, the exponential map (Riemannian geometry), exponential map maps the tangent space at a point of a differentiable manifold, manifold to a neighborhood (mathematics), neighborhood of that point. Its inverse is also called the logarithmic (or log) map.
In the context of finite groups exponentiation is given by repeatedly multiplying one group element with itself. The
discrete logarithm
In mathematics, for given real numbers ''a'' and ''b'', the logarithm log''b'' ''a'' is a number ''x'' such that . Analogously, in any group ''G'', powers ''b'k'' can be defined for all integers ''k'', and the discrete logarithm log''b' ...
is the integer ' solving the equation
:
where is an element of the group. Carrying out the exponentiation can be done efficiently, but the discrete logarithm is believed to be very hard to calculate in some groups. This asymmetry has important applications in public key cryptography, such as for example in the Diffie–Hellman key exchange, a routine that allows secure exchanges of cryptography, cryptographic keys over unsecured information channels. Zech's logarithm is related to the discrete logarithm in the multiplicative group of non-zero elements of a finite field.
Further logarithm-like inverse functions include the ''double logarithm'' , the ''super-logarithm, super- or hyper-4-logarithm'' (a slight variation of which is called iterated logarithm in computer science), the Lambert W function, and the logit. They are the inverse functions of the double exponential function, tetration, of , and of the logistic function, respectively.
Related concepts
From the perspective of group theory, the identity expresses a group isomorphism between positive real number, reals under multiplication and reals under addition. Logarithmic functions are the only continuous isomorphisms between these groups. By means of that isomorphism, the Haar measure (Lebesgue measure) on the reals corresponds to the Haar measure on the positive reals. The non-negative reals not only have a multiplication, but also have addition, and form a semiring, called the probability semiring; this is in fact a semifield. The logarithm then takes multiplication to addition (log multiplication), and takes addition to log addition (LogSumExp), giving an isomorphism of semirings between the probability semiring and the log semiring.
logarithmic form, Logarithmic one-forms appear in complex analysis and algebraic geometry as differential forms with logarithmic Pole (complex analysis), poles.
The polylogarithm is the function defined by
:
It is related to the
natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
by . Moreover, equals the Riemann zeta function .
See also
* Decimal exponent (dex)
* Exponential function
* Index of logarithm articles
Notes
References
External links
*
*
*
*
Khan Academy: Logarithms, free online micro lectures*
*
*
*
{{Authority control
Logarithms,
Elementary special functions
Scottish inventions
Additive functions
 In
In 
 Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using power series or the arithmetic–geometric mean, or be retrieved from a precalculated logarithm table that provides a fixed precision.
Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using power series or the arithmetic–geometric mean, or be retrieved from a precalculated logarithm table that provides a fixed precision. 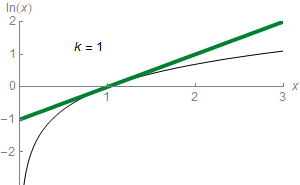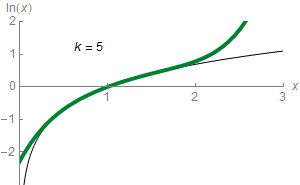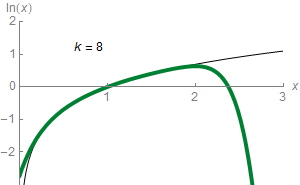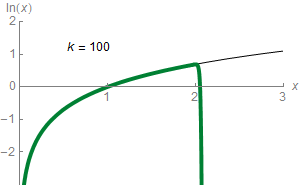 For any real number that satisfies , the following formula holds:
:
This is a shorthand for saying that can be approximated to a more and more accurate value by the following expressions:
:
For example, with the third approximation yields 0.4167, which is about 0.011 greater than . This series approximates with arbitrary precision, provided the number of summands is large enough. In elementary calculus, is therefore the
For any real number that satisfies , the following formula holds:
:
This is a shorthand for saying that can be approximated to a more and more accurate value by the following expressions:
:
For example, with the third approximation yields 0.4167, which is about 0.011 greater than . This series approximates with arbitrary precision, provided the number of summands is large enough. In elementary calculus, is therefore the  Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of scale invariance. For example, each chamber of the shell of a nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a logarithmic spiral. Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.
Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of scale invariance. For example, each chamber of the shell of a nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a logarithmic spiral. Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.