|
Rapidity
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates. For one-dimensional motion, rapidities are additive whereas velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite. Using the inverse hyperbolic function , the rapidity corresponding to velocity is where ''c'' is the velocity of light. For low speeds, is approximately . Since in relativity any velocity is constrained to the interval the ratio satisfies . The inverse hyperbolic tangent has the unit interval for its domain and the whole real line for its image; that is, the interval maps onto . History In 1908 Hermann Minkowski ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from 1, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Transformation
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity-addition Formula
In relativistic physics, a velocity-addition formula is a three-dimensional equation that relates the velocities of objects in different reference frames. Such formulas apply to successive Lorentz transformations, so they also relate different frames. Accompanying velocity addition is a kinematic effect known as Thomas precession, whereby successive non-collinear Lorentz boosts become equivalent to the composition of a rotation of the coordinate system and a boost. Standard applications of velocity-addition formulas include the Doppler shift, Doppler navigation, the aberration of light, and the dragging of light in moving water observed in the 1851 Fizeau experiment. The notation employs as velocity of a body within a Lorentz frame , and as velocity of a second frame , as measured in , and as the transformed velocity of the body within the second frame. History The speed of light in a fluid is slower than the speed of light in vacuum, and it changes if the fluid is moving a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
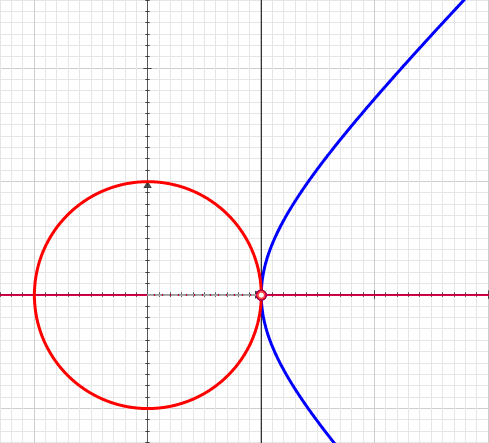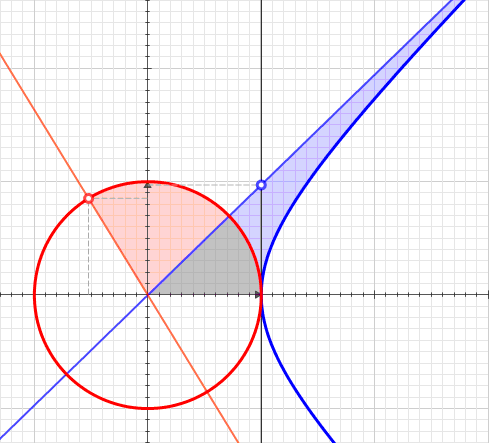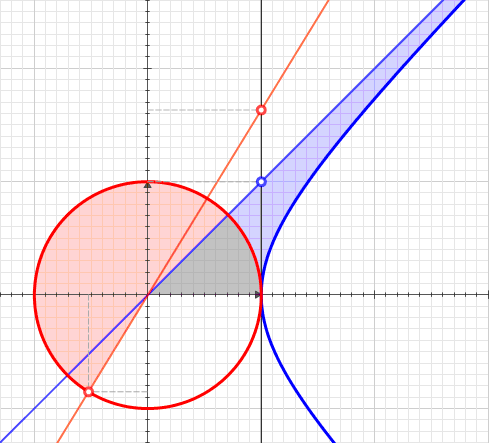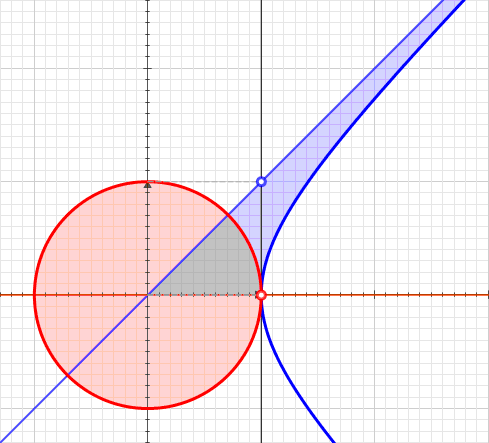
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of \sqrt 2, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Hyperbola
In geometry, the unit hyperbola is the set of points (''x'',''y'') in the Cartesian plane that satisfy the implicit equation x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an ''alternative radial length'' : r = \sqrt . Whereas the unit circle surrounds its center, the unit hyperbola requires the ''conjugate hyperbola'' y^2 - x^2 = 1 to complement it in the plane. This pair of hyperbolas share the asymptotes ''y'' = ''x'' and ''y'' = −''x''. When the conjugate of the unit hyperbola is in use, the alternative radial length is r = \sqrt . The unit hyperbola is a special case of the rectangular hyperbola, with a particular orientation, location, and scale. As such, its eccentricity equals \sqrt. The unit hyperbola finds applications where the circle must be replaced with the hyperbola for purposes of analytic geometry. A prominent instance is the depiction of spacetime as a pseudo-Euclidean space. There the asymptotes of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vladimir Varićak
Vladimir Varićak (sometimes also spelled Vladimir Varičak; March 1, 1865 – January 17, 1942) was a Croatian mathematician and theoretical physicist of Serbian origin.Buljan I.; Paušek-Baždar, Snježana. "Hrvatski matematički velikan koji je otkrio Ruđera", ''Školske novine'', 8 May 2018, no. 17 (2018), p. 24Paušek-Baždar; Ilakovac, Ksenofont. "Akademik Vladimir Varićak u hrvatskoj i svjetskoj znanosti", Croatian Academy of Sciences and Arts, 2018., 247 p. Biography Varićak, an ethnic Serb, was born on March 1, 1865 in the village of Švica near Otočac, Austrian Empire (present-day Croatia). He studied physics and mathematics at the University of Zagreb from 1883 to 1887. He made his PhD in 1889 and got his habilitation in 1895. In 1899 he became professor of mathematics in Zagreb, where he gave lectures until his death in 1942. From 1903 to 1908 he wrote on hyperbolic geometry (or Bolyai– Lobachevskian geometry). In 1910, following a 1909 publication of Sommer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Rotation
In linear algebra, a squeeze mapping, also called a squeeze transformation, is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is ''not'' a rotation or shear mapping. For a fixed positive real number , the mapping :(x, y) \mapsto (ax, y/a) is the ''squeeze mapping'' with parameter . Since :\ is a hyperbola, if and , then and the points of the image of the squeeze mapping are on the same hyperbola as is. For this reason it is natural to think of the squeeze mapping as a hyperbolic rotation, as did Émile Borel in 1914, by analogy with ''circular rotations'', which preserve circles. Logarithm and hyperbolic angle The squeeze mapping sets the stage for development of the concept of logarithms. The problem of finding the area bounded by a hyperbola (such as is one of quadrature. The solution, found by Grégoire de Saint-Vincent and Alphonse Antonio de Sarasa in 1647, required the natural logarithm function, a new concept. Some ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Robb
Alfred Arthur Robb FRS (18 January 1873 in Belfast – 14 December 1936 in Castlereagh) was a Northern Irish physicist. Biography Robb studied at Queen's College, Belfast (BA 1894) and at St John's College, Cambridge (Tripos 1897, MA 1901). He then proceeded to University of Göttingen, where, guided by Woldemar Voigt, he wrote his dissertation on the Zeeman effect. He also worked under J. J. Thomson at the Cavendish Laboratory. The Croix de Guerre was awarded to him for WWI service in the Red Cross, and in 1921 he became a fellow of the Royal Society. He is known for his four books on special relativity (1911, 1914, 1921, 1936) where he gave a spacetime derivation of the theory in an axiomatic-geometric way. Robb therefore was sometimes called the "Euclid of relativity". In the first of these works he used a hyperbolic angle ω to introduce the concept of rapidityRobb (1911) ''Optical Geometry of Motion'' and showed that the kinematic space of velocities is hyper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frames Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate axes. In Einsteinian relativity, reference frames are used to specify the relationship between a moving observer and the phenomenon under observation. In this context, the term often becomes observational frame of reference (or observational reference frame), which implies that the observer is at rest in the frame, although not necessarily located at its origin. A rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relativistic Velocity
Relativistic speed refers to speed at which relativistic effects become significant to the desired accuracy of measurement of the phenomenon being observed. Relativistic effects are those discrepancies between values calculated by models considering and not considering relativity. Related words are velocity, rapidity, and celerity which is proper velocity. Speed is a scalar, being the magnitude of the velocity vector which in relativity is the four-velocity and in three-dimension Euclidean space a three-velocity. Speed is empirically measured as average speed, although current devices in common use can estimate speed over very small intervals and closely approximate instantaneous speed. Non-relativistic discrepancies include cosine error which occurs in speed detection devices when only one scalar component of the three-velocity is measured and the Doppler effect which may affect observations of wavelength and frequency. Relativistic effects are highly non-linear and for every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime Diagram
A spacetime diagram is a graphical illustration of the properties of space and time in the special theory of relativity. Spacetime diagrams allow a qualitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical equations. The history of an object's location throughout all time traces out a line, referred to as the object's world line, in a spacetime diagram. Points in spacetime diagrams represent a fixed position in space and time and are referred to as events. The most well-known class of spacetime diagrams are known as Minkowski diagrams, developed by Hermann Minkowski in 1908. Minkowski diagrams are two-dimensional graphs that depict events as happening in a universe consisting of one space dimension and one time dimension. Unlike a regular distance-time graph, the distance is displayed on the horizontal axis and time on the vertical axis. Additionally, the time and space units of measurement are chosen in such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A History Of The Theories Of Aether And Electricity
''A History of the Theories of Aether and Electricity'' is any of three books written by British mathematician Sir Edmund Taylor Whittaker FRS FRSE on the history of electromagnetic theory, covering the development of classical electromagnetism, optics, and aether theories. The book's first edition, subtitled ''from the Age of Descartes to the Close of the Nineteenth Century'', was published in 1910 by Longmans, Green. The book covers the history of aether theories and the development of electromagnetic theory up to the 20th century. A second, extended and revised, edition consisting of two volumes was released in the early 1950s by Thomas Nelson, expanding the book's scope to include the first quarter of the 20th century. The first volume, subtitled ''The Classical Theories'', was published in 1951 and served as a revised and updated edition to the first book. The second volume, subtitled ''The Modern Theories (1900–1926)'', was published two years later in 1953, extended ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |