|
Phase-space Formulation
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
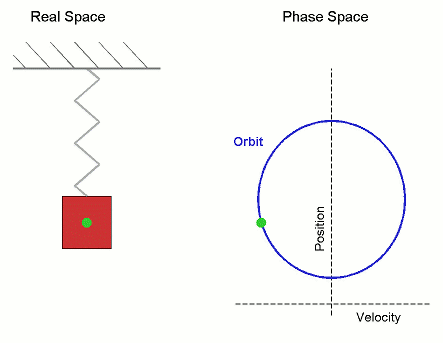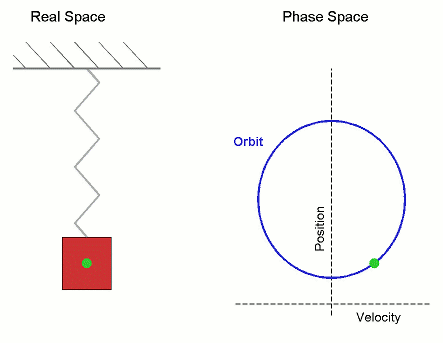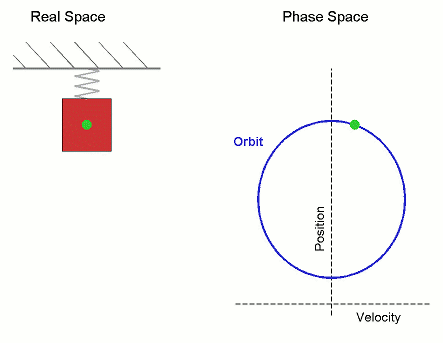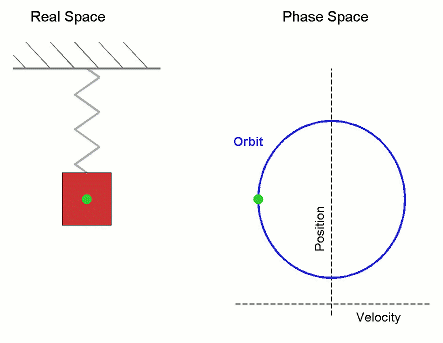
Simple Harmonic Motion Orbit
Simple or SIMPLE may refer to: *Simplicity, the state or quality of being simple Arts and entertainment * Simple (album), ''Simple'' (album), by Andy Yorke, 2008, and its title track * Simple (Florida Georgia Line song), "Simple" (Florida Georgia Line song), 2018 * "Simple", a song by Johnny Mathis from the 1984 album ''A Special Part of Me'' * "Simple", a song by Collective Soul from the 1995 album ''Collective Soul (1995 album), Collective Soul'' * "Simple", a song by Katy Perry from the 2005 soundtrack to ''The Sisterhood of the Traveling Pants (film), The Sisterhood of the Traveling Pants'' * "Simple", a song by Khalil from the 2017 album ''Prove It All'' * "Simple", a song by Kreesha Turner from the 2008 album ''Passion (Kreesha Turner album), Passion'' * "Simple", a song by Ty Dolla Sign from the 2017 album ''Beach House 3'' deluxe version * Simple (video game series), ''Simple'' (video game series), budget-priced console games Businesses and organisations * Simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Robotic Arm
A robotic arm is a type of mechanical arm, usually programmable, with similar functions to a human arm; the arm may be the sum total of the mechanism or may be part of a more complex robot. The links of such a manipulator are connected by joints allowing either rotational motion (such as in an articulated robot) or translational (linear) displacement. The links of the manipulator can be considered to form a kinematic chain. The terminus of the kinematic chain of the manipulator is called the end effector and it is analogous to the human hand. However, the term "robotic hand" as a synonym of the robotic arm is often proscribed. Types * Cartesian robot / Gantry robot: Used for pick and place work, application of sealant, assembly operations, handling machine tools and arc welding. It is a robot whose arm has three prismatic joints, whose axes are coincident with a Cartesian coordinator. * Collaborative robot / Cobot: Cobot applications contrast with traditional industri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exponential Growth Model
Population growth is the increase in the number of people in a population or dispersed group. The World population, global population has grown from 1 billion in 1800 to 8.2 billion in 2025. Actual global human population growth amounts to around 70 million annually, or 0.85% per year. As of 2024, The United Nations projects that global population will peak in the mid-2080s at around 10.3 billion. The UN's estimates have decreased strongly in recent years due to sharp declines in global birth rates. Others have challenged many recent population projections as having underestimated population growth. The world human population has been growing since the end of the Black Death, around the year 1350. A mix of technological advancement that improved agricultural productivity and sanitation and medical advancement that reduced mortality increased population growth. In some geographies, this has slowed through the process called the demographic transition, where many nations with high ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable (mathematics), variable. As with any other DE, its unknown(s) consists of one (or more) Function (mathematics), function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equation, ''partial'' differential equations (PDEs) which may be with respect to one independent variable, and, less commonly, in contrast with stochastic differential equations, ''stochastic'' differential equations (SDEs) where the progression is random. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where a_0(x),\ldots,a_n(x) and b(x) are arbitrary differentiable functions that do not need to be linea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Autonomous System (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a simultaneous equations, system of ordinary differential equations which does not explicitly depend on the independent variable. When the variable is time, they are also called time-invariant systems. Many laws in physics, where the independent variable is usually assumed to be time, are expressed as autonomous systems because it is assumed the Physical law, laws of nature which hold now are identical to those for any point in the past or future. Definition An autonomous system is a system of ordinary differential equations of the form \fracx(t)=f(x(t)) where takes values in -dimensional Euclidean space; is often interpreted as time. It is distinguished from systems of differential equations of the form \fracx(t)=g(x(t),t) in which the law governing the evolution of the system does not depend solely on the system's current state but also the parameter , again often interpreted as time; such system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Liouville's Theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical mechanics, statistical and Hamiltonian mechanics. It asserts that ''the phase space, phase-space distribution function is constant along the Trajectory, trajectories of the system''—that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time. This time-independent density is in statistical mechanics known as the classical a priori probability. Liouville's theorem applies to conservative systems, that is, systems in which the effects of friction are absent or can be ignored. The general mathematical formulation for such systems is the measure-preserving dynamical system. Liouville's theorem applies when there are degrees of freedom that can be interpreted as positions and momenta; not all measure-preserving dynamical systems have these, but Hamiltonian systems do. The general se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistical Ensemble (mathematical Physics)
In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902. A thermodynamic ensemble is a specific variety of statistical ensemble that, among other properties, is in statistical equilibrium (defined below), and is used to derive the properties of thermodynamic systems from the laws of classical or quantum mechanics. Physical considerations The ensemble formalises the notion that an experimenter repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symplectic Structure
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold. The term "symplectic", introduced by Hermann Weyl, is a calque of "complex"; previously, the "symplectic group" had been called the "line complex group". "Complex" comes from the Latin ''com-plexus'', meaning "braided together" (co- + plexus), while symplectic comes from the corresponding Greek ''sym-plektikos'' (συμπλεκτικός); in both cases the stem comes from the Indo-European root *pleḱ- The name reflects the deep connections between complex and symplectic structures. By Darboux's theorem, symplectic manifolds are isomorphic to the standard symplectic vector space locally, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Darboux Coordinates
In differential geometry, a field in mathematics, Darboux's theorem is a theorem providing a normal form for special classes of differential 1-forms, partially generalizing the Frobenius integration theorem. It is named after Jean Gaston Darboux who established it as the solution of the Pfaff problem. It is a foundational result in several fields, the chief among them being symplectic geometry. Indeed, one of its many consequences is that any two symplectic manifolds of the same dimension are locally symplectomorphic to one another. That is, every 2n -dimensional symplectic manifold can be made to look locally like the linear symplectic space \mathbb^n with its canonical symplectic form. There is also an analogous consequence of the theorem applied to contact geometry. Statement Suppose that \theta is a differential 1-form on an ''n ''-dimensional manifold, such that \mathrm \theta has constant rank ''p ''. Then * if \theta \wedge \left(\mathrm\theta\right)^p = 0 e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cotangent Bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold. It may be described also as the dual bundle to the tangent bundle. This may be generalized to categories with more structure than smooth manifolds, such as complex manifolds, or (in the form of cotangent sheaf) algebraic varieties or schemes. In the smooth case, any Riemannian metric or symplectic form gives an isomorphism between the cotangent bundle and the tangent bundle, but they are not in general isomorphic in other categories. Formal definition via diagonal morphism There are several equivalent ways to define the cotangent bundle. One way is through a diagonal mapping Δ and germs. Let ''M'' be a smooth manifold and let ''M''×''M'' be the Cartesian product of ''M'' with itself. The diagonal mapping Δ sends a point ''p'' in ''M'' to the point (''p'',''p'') of ''M''×''M'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conjugate Momentum
Conjugation or conjugate may refer to: Linguistics *Grammatical conjugation, the modification of a verb from its basic form * Emotive conjugation or Russell's conjugation, the use of loaded language Mathematics *Complex conjugation, the change of sign of the imaginary part of a complex number * Conjugate (square roots), the change of sign of a square root in an expression *Conjugate element (field theory), a generalization of the preceding conjugations to roots of a polynomial of any degree * Conjugate transpose, the complex conjugate of the transpose of a matrix * Harmonic conjugate in complex analysis * Conjugate (graph theory), an alternative term for a line graph, i.e. a graph representing the edge adjacencies of another graph *In group theory, various notions are called conjugation: ** Inner automorphism, a type of conjugation homomorphism **Conjugacy class in group theory, related to matrix similarity in linear algebra ** Conjugation (group theory), the image of an elemen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |