|
Particular Values Of The Gamma Function
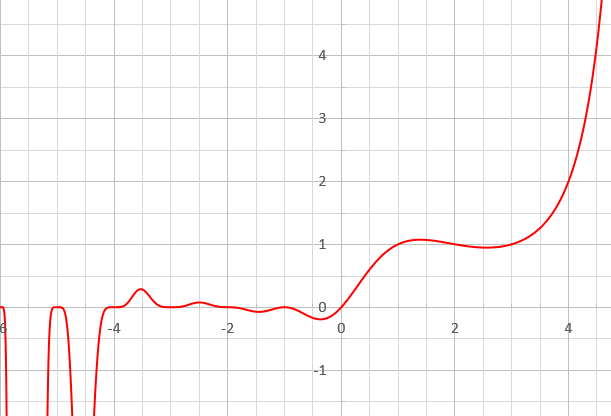
The gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer arguments, but no simple expressions are known for the values at rational points in general. Other fractional arguments can be approximated through efficient infinite products, infinite series, and recurrence relations. Integers and half-integers For positive integer arguments, the gamma function coincides with the factorial. That is, :\Gamma(n) = (n-1)!, and hence :\begin \Gamma(1) &= 1, \\ \Gamma(2) &= 1, \\ \Gamma(3) &= 2, \\ \Gamma(4) &= 6, \\ \Gamma(5) &= 24, \end and so on. For non-positive integers, the gamma function is not defined. For positive half-integers, the function values are given exactly by :\Gamma \left (\tfrac \right) = \sqrt \pi \frac\,, or equivalently, for non-negative integer values of : :\begin \Gamma\left(\tfrac12+n\right) &= \frac\, \sqrt = \frac \sqrt \\ \Gamma\left(\tfrac12-n\right) &= \frac\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M \ (z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the function at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulus Squared
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 (caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is '' quadratic''. The square of an integer may also be called a square number or a perfect square. In algebra, the operation of squaring is often generalized to polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial is the quadratic polynomial . One of the important properties of squaring, for numbers as well as in many other mathematical systems, is that (for all nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Formula
In mathematics, a reflection formula or reflection relation for a function ''f'' is a relationship between ''f''(''a'' − ''x'') and ''f''(''x''). It is a special case of a functional equation, and it is very common in the literature to use the term "functional equation" when "reflection formula" is meant. Reflection formulas are useful for numerical computation of special functions. In effect, an approximation that has greater accuracy or only converges on one side of a reflection point (typically in the positive half of the complex plane) can be employed for all arguments. Known formulae The even and odd functions satisfy by definition simple reflection relations around ''a'' = 0. For all even functions, :f(-x) = f(x), and for all odd functions, :f(-x) = -f(x). A famous relationship is Euler's reflection formula :\Gamma(z)\Gamma(1-z) = \frac, \qquad z \not\in \mathbb Z for the gamma function \Gamma(z), due to Leonhard Euler. There is also a reflect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. If the latter is defined as the largest integer not greater than , called floor of or \lfloor x\rfloor, its fractional part can be written as: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the Weisstein,_Eric_W._"Fractional_Part."_From_MathWorld--A_Wolfram_Web_Resource /ref> : |
Barnes G-function
In mathematics, the Barnes G-function ''G''(''z'') is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function. Formally, the Barnes ''G''-function is defined in the following Weierstrass product form: : G(1+z)=(2\pi)^ \exp\left(- \frac \right) \, \prod_^\infty \left\ where \, \gamma is the Euler–Mascheroni constant, exp(''x'') = ''e''''x'' is the exponential function, and Π denotes multiplication (capital pi notation). As an entire function, ''G'' is of order two, and of infinite type. This can be deduced from the asymptotic expansion given below. Functional equation and integer arguments The Barnes ''G''-function satisfies the functional equation : G(z+1)=\Gamma(z)\, G(z) with normalisation ''G''(1) = 1. Note the similarity between the functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Unit
The imaginary unit or unit imaginary number () is a solution to the quadratic equation x^2+1=0. Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition and multiplication. A simple example of the use of in a complex number is 2+3i. Imaginary numbers are an important mathematical concept; they extend the real number system \mathbb to the complex number system \mathbb, in which at least one root for every nonconstant polynomial exists (see Algebraic closure and Fundamental theorem of algebra). Here, the term "imaginary" is used because there is no real number having a negative square. There are two complex square roots of −1: and -i, just as there are two complex square roots of every real number other than zero (which has one double square root). In contexts in which use of the letter is ambiguous or problematic, the letter or the Greek \iota is sometimes used instead. For example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theta Function
In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory. The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables (conventionally called ), a theta function has a property expressing its behavior with respect to the addition of a period of the associated elliptic functions, making it a quasiperiodic function. In the abstract theory this quasiperiodicity comes from the cohomology class of a line bundle on a complex torus, a condition of descent. One interpretation of theta functions when dealing with the heat equation is that "a theta function is a special function that describes the evolution of temperature on a segment domain subject to certain boundary conditions". Throughout this article, (e^)^ should b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan's Constant
In mathematics, Catalan's constant , is defined by : G = \beta(2) = \sum_^ \frac = \frac - \frac + \frac - \frac + \frac - \cdots, where is the Dirichlet beta function. Its numerical value is approximately : It is not known whether is irrational number, irrational, let alone transcendental number, transcendental. has been called "arguably the most basic constant whose irrationality and transcendence (though strongly suspected) remain unproven". Catalan's constant was named after Eugène Charles Catalan, who found quickly-converging series for its calculation and published a memoir on it in 1865. Uses In low-dimensional topology, Catalan's constant is 1/4 of the volume of an ideal polyhedron, ideal hyperbolic octahedron, and therefore 1/4 of the hyperbolic volume of the complement of the Whitehead link. It is 1/8 of the volume of the complement of the Borromean rings. In combinatorics and statistical mechanics, it arises in connection with counting domino tilings, spannin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glaisher–Kinkelin Constant
In mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted , is a mathematical constant, related to the -function and the Barnes -function. The constant appears in a number of sums and integrals, especially those involving gamma functions and zeta functions. It is named after mathematicians James Whitbread Lee Glaisher and Hermann Kinkelin. Its approximate value is: : = ... . The Glaisher–Kinkelin constant can be given by the limit: :A=\lim_ \frac where is the hyperfactorial. This formula displays a similarity between and which is perhaps best illustrated by noting Stirling's formula: :\sqrt=\lim_ \frac which shows that just as is obtained from approximation of the factorials, can also be obtained from a similar approximation to the hyperfactorials. An equivalent definition for involving the Barnes -function, given by where is the gamma function is: :A=\lim_ \frac. The Glaisher–Kinkelin constant also appears in evaluations of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Product
In mathematics, for a sequence of complex numbers ''a''1, ''a''2, ''a''3, ... the infinite product : \prod_^ a_n = a_1 a_2 a_3 \cdots is defined to be the limit of a sequence, limit of the Multiplication#Capital pi notation, partial products ''a''1''a''2...''a''''n'' as ''n'' increases without bound. The product is said to ''Limit of a sequence, converge'' when the limit exists and is not zero. Otherwise the product is said to ''diverge''. A limit of zero is treated specially in order to obtain results analogous to those for Infinite series, infinite sums. Some sources allow convergence to 0 if there are only a finite number of zero factors and the product of the non-zero factors is non-zero, but for simplicity we will not allow that here. If the product converges, then the limit of the sequence ''a''''n'' as ''n'' increases without bound must be 1, while the converse is in general not true. The best known examples of infinite products are probably some of the formulae for pi, &p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |