Fractional part

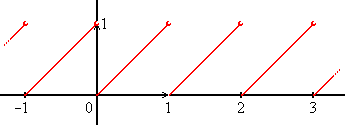The fractional part or decimal part of a non‐negative real number $x$ is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than , called ''floor'' of or $\lfloor x\rfloor$. Then, the fractional part can be formulated as a difference:

:$\operatorname (x)=x - \lfloor x \rfloor,\; x > 0$.

The fractional part of logarithms, specifically, is also known as the mantissa; by contrast with the mantissa, the integral part of a logarithm is called its ''characteristic''. The word ''mantissa'' was introduced by Henry Briggs.

For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point, such as the decimal point in English. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the Weisstein, Eric W. "Fractional Part." From MathWorld--A Wolfram Web Resource
/ref>

:$\operatorname (x)=\begin x - \lfloor x \rfloor & x \ge 0 \\ x - \lceil x \rceil & x < 0 \end$

with $\lceil x \rceil$ as the smallest integer not less than , also called the ceiling of . By consequence, we may get, for example, three different values for the fractional part of just one : let it be −1.3, its fractional part will be 0.7 according to the first definition, 0.3 according to the second definition, and −0.3 according to the third definition, whose result can also be obtained in a straightforward way by
:$\operatorname (x)= x - \lfloor ">x, \rfloor \cdot \sgn(x)$.

The $x - \lfloor x \rfloor$ and the "odd function" definitions permit for unique decomposition of any real number to the addition, sum of its integer and fractional parts, where "integer part" refers to $\lfloor x \rfloor$ or $\lfloor , x, \rfloor \cdot \sgn(x)$ respectively. These two definitions of fractional-part function also provide idempotence.

The fractional part defined via difference from floor function, ⌊ ⌋ is usually denoted by curly braces:
:$\ := x-\lfloor x \rfloor.$

Relation to continued fractions

Every real number can be essentially uniquely represented as a simple continued fraction, namely as the sum of its integer part and the reciprocal of its fractional part which is written as the sum of ''its'' integer part and the reciprocal of ''its'' fractional part, and so on.

See also

* Circle group
* Equidistributed sequence
* One-parameter group
* Pisot–Vijayaraghavan number
* Poussin proof
* Significand

References

{{Reflist

Arithmetic
Unary operations