|
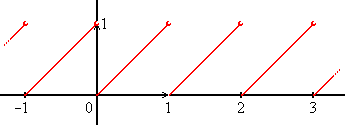
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than , called ''floor'' of or \lfloor x\rfloor. Then, the fractional part can be formulated as a difference: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. The fractional part of logarithms, specifically, is also known as the mantissa; by contrast with the mantissa, the integral part of a logarithm is called its ''characteristic''. The word ''mantissa'' was introduced by Henry Briggs. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point, such as the decimal point in English. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parte Fraccionaria
Parte is the Italian word for part. It can refer to: * Part (music) * Conjugation of French verb "partir"; see French conjugation ;Surname * Víctor de la Parte Víctor de la Parte González (born 22 June 1986) is a Spanish cyclist, who currently rides for UCI ProTeam . He was named in the start list for the 2017 Giro d'Italia. In August 2019, he was named in the startlist for the 2019 Vuelta a España. ... (b. 1986), Spanish cyclist See also * Ex parte, Latin legal term for "by the party" {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Function
In mathematics, an even function is a real function such that f(-x)=f(x) for every x in its domain. Similarly, an odd function is a function such that f(-x)=-f(x) for every x in its domain. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = x^n is even if ''n'' is an even integer, and it is odd if ''n'' is an odd integer. Even functions are those real functions whose graph is self-symmetric with respect to the and odd functions are those whose graph is self-symmetric with respect to the origin. If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function. Early history The concept of even and odd functions appears to date back to the early 18th century, with Leonard Euler playing a significant role in their formalization. Euler introduced the concepts of even and odd functions (using Lati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significand
The significand (also coefficient, sometimes argument, or more ambiguously mantissa, fraction, or characteristic) is the first (left) part of a number in scientific notation or related concepts in floating-point representation, consisting of its significant digits. For negative numbers, it does not include the initial minus sign. Depending on the interpretation of the exponent, the significand may represent an integer or a fractional number, which may cause the term "mantissa" to be misleading, since the ''mantissa'' of a logarithm is always its fractional part. Although the other names mentioned are common, ''significand'' is the word used by IEEE 754, an important technical standard for floating-point arithmetic. In mathematics, the term "argument" may also be ambiguous, since "the argument of a number" sometimes refers to the length of a circular arc from 1 to a number on the unit circle in the complex plane. Example The number 123.45 can be represented as a decimal floati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poussin Proof
In number theory, a branch of mathematics, the Poussin proof is the proof of an identity related to the fractional part of a ratio. In 1838, Peter Gustav Lejeune Dirichlet proved an approximate formula for the average number of divisors of all the numbers from 1 to n: :\frac \approx \ln n + 2\gamma - 1, where ''d'' represents the divisor function, and γ represents the Euler-Mascheroni constant. In 1898, Charles Jean de la Vallée-Poussin proved that if a large number n is divided by all the primes up to n, then the average fraction by which the quotient falls short of the next whole number is γ: :\frac \approx1- \gamma, where represents the fractional part of ''x'', and π represents the prime-counting function In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number . It is denoted by (unrelated to the number ). A symmetric variant seen sometimes is , which is equal .... For example, if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pisot–Vijayaraghavan Number
In mathematics, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real algebraic integer greater than 1, all of whose Galois conjugates are less than 1 in absolute value. These numbers were discovered by Axel Thue in 1912 and rediscovered by G. H. Hardy in 1919 within the context of Diophantine approximation. They became widely known after the publication of Charles Pisot's dissertation in 1938. They also occur in the uniqueness problem for Fourier series. Tirukkannapuram Vijayaraghavan and Raphael Salem continued their study in the 1940s. Salem numbers are a closely related set of numbers. A characteristic property of PV numbers is that their powers approach integers at an exponential rate. Pisot proved a remarkable converse: if ''α'' > 1 is a real number such that the sequence : \, \alpha^n\, measuring the distance from its consecutive powers to the nearest integer is square-summable, or ''ℓ'' 2, then ''α'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-parameter Group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphism :\varphi : \mathbb \rightarrow G from the real line \mathbb (as an additive group) to some other topological group G. If \varphi is injective then \varphi(\mathbb), the image, will be a subgroup of G that is isomorphic to \mathbb as an additive group. One-parameter groups were introduced by Sophus Lie in 1893 to define infinitesimal transformations. According to Lie, an ''infinitesimal transformation'' is an infinitely small transformation of the one-parameter group that it generates. It is these infinitesimal transformations that generate a Lie algebra that is used to describe a Lie group of any dimension. The action of a one-parameter group on a set is known as a flow. A smooth vector field on a manifold, at a point, induces a ''local flow'' - a one parameter group of local diffeomorphisms, sending points along integral curves of the vector field. The local flow of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equidistributed Sequence
In mathematics, a sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that subinterval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration. Definition A sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be ''equidistributed'' on a non-degenerate interval 'a'', ''b''if for every subinterval 'c'', ''d''of 'a'', ''b''we have :\lim_= . (Here, the notation , ∩ 'c'', ''d'' denotes the number of elements, out of the first ''n'' elements of the sequence, that are between ''c'' and ''d''.) For example, if a sequence is equidistributed in , 2 since the interval .5, 0.9occupies 1/5 of the length of the interval , 2 as ''n'' becomes large, the proportion of the first ''n'' members of the sequence which fall between 0.5 and 0.9 must approach 1/5. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Group
In mathematics, the circle group, denoted by \mathbb T or , is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers \mathbb T = \. The circle group forms a subgroup of , the multiplicative group of all nonzero complex numbers. Since \C^\times is abelian, it follows that \mathbb T is as well. A unit complex number in the circle group represents a rotation of the complex plane about the origin and can be parametrized by the angle measure : \theta \mapsto z = e^ = \cos\theta + i\sin\theta. This is the exponential map for the circle group. The circle group plays a central role in Pontryagin duality and in the theory of Lie groups. The notation \mathbb T for the circle group stems from the fact that, with the standard topology (see below), the circle group is a 1-torus. More generally, \mathbb T^n (the direct product of \mathbb T with itself n times) is geometrically an n-toru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal (mathematics)
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an involution). Multiplying by a number is the same as dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yields the original number (since the product of the number and its reciprocal is 1). The term ''reciproca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Continued Fraction
A simple or regular continued fraction is a continued fraction with numerators all equal one, and denominators built from a sequence \ of integer numbers. The sequence can be finite or infinite, resulting in a finite (or terminated) continued fraction like :a_0 + \cfrac or an infinite continued fraction like :a_0 + \cfrac Typically, such a continued fraction is obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In the ''finite'' case, the iteration/recursion is stopped after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an ''infinite'' continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. Simple co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curly Brace
Curly is a surname, given name, nickname or stage name. It may refer to: First name, nickname or stage name * Crazy Horse (1840–1877), Oglala Sioux war chief nicknamed "Curly" * Curly (scout), nickname of Ashishishe (1923), Crow Indian scout for General Custer * Paul Carlyle Curly Armstrong (1918–1983), American basketball player * Curly Bill Brocius, nickname of William Brocius (1882), American Old West gunman and outlaw * Charles Roy Curly Brown (1888–1968), American Major League Baseball pitcher * Harold Lee Curly Chalker (1931–1998), American country and jazz musician * Robert F. Curly Clement (1919–2006), American baseball umpire * Curly Ray Cline (1923–1997), American bluegrass fiddler * Curly, nickname of George Andrew Davis Jr. (1920–1952), American World War II and Korean War flying ace * Curly Joe DeRita, Three Stooges persona of Joseph Wardell, whose stage name was Joe DeRita (1909–1993), American actor and comedian * Clarence T. "Curly" Edwin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Idempotence
Idempotence (, ) is the property of certain operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of places in abstract algebra (in particular, in the theory of projectors and closure operators) and functional programming (in which it is connected to the property of referential transparency). The term was introduced by American mathematician Benjamin Peirce in 1870 in the context of elements of algebras that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from + '' potence'' (same + power). Definition An element x of a set S equipped with a binary operator \cdot is said to be ''idempotent'' under \cdot if : . The ''binary operation'' \cdot is said to be ''idempotent'' if : . Examples * In the monoid (\mathbb, \times) of the natural numbers with multiplication, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |