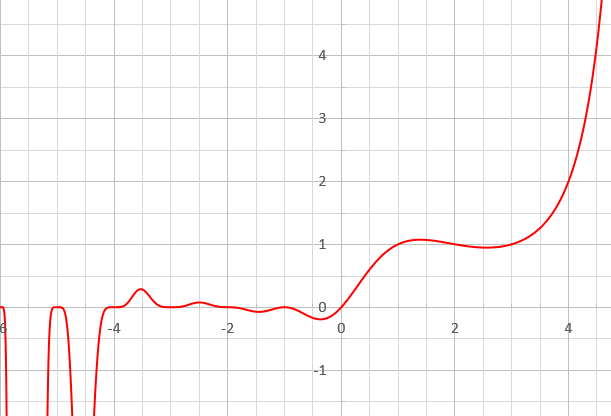
|
Barnes G-function
In mathematics, the Barnes G-function ''G''(''z'') is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function. Formally, the Barnes ''G''-function is defined in the following Weierstrass product form: : G(1+z)=(2\pi)^ \exp\left(- \frac \right) \, \prod_^\infty \left\ where \, \gamma is the Euler–Mascheroni constant, exp(''x'') = ''e''''x'' is the exponential function, and Π denotes multiplication (capital pi notation). As an entire function, ''G'' is of order two, and of infinite type. This can be deduced from the asymptotic expansion given below. Functional equation and integer arguments The Barnes ''G''-function satisfies the functional equation : G(z+1)=\Gamma(z)\, G(z) with normalisation ''G''(1) = 1. Note the similarity between the functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plot Of The Barnes G Aka Double Gamma Function G(z) In The Complex Plane From -2-2i To 2+2i With Colors Created With Mathematica 13
Plot or Plotting may refer to: Art, media and entertainment * Plot (narrative), the story of a piece of fiction Music * ''The Plot'' (album), a 1976 album by jazz trumpeter Enrico Rava * The Plot (band), a band formed in 2003 Other * ''Plot'' (film), a 1973 French-Italian film * ''Plotting'' (video game), a 1989 Taito puzzle video game, also called Flipull * ''The Plot'' (video game), a platform game released in 1988 for the Amstrad CPC and Sinclair Spectrum * ''Plotting'' (non-fiction), a 1939 book on writing by Jack Woodford * ''The Plot'' (novel), a 2021 mystery by Jean Hanff Korelitz Graphics * Plot (graphics), a graphical technique for representing a data set * Plot (radar), a graphic display that shows all collated data from a ship's on-board sensors * Plot plan, a type of drawing which shows existing and proposed conditions for a given area Land * Plot (land), a piece of land used for building on ** Burial plot, a piece of land a person is buried in * Quadrat, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Equation
In mathematics, a functional equation is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning is often used, where a ''functional equation'' is an equation that relates several values of the same function. For example, the logarithm functions are essentially characterized by the ''logarithmic functional equation'' \log(xy)=\log(x) + \log(y). If the domain of the unknown function is supposed to be the natural numbers, the function is generally viewed as a sequence, and, in this case, a functional equation (in the narrower meaning) is called a recurrence relation. Thus the term ''functional equation'' is used mainly for real functions and complex functions. Moreover a smoothness condition is often assumed for the solutions, since without such a condition, most functional equations have very irregular solutions. For example, the ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor's Theorem
In calculus, Taylor's theorem gives an approximation of a ''k''-times differentiable function around a given point by a polynomial of degree ''k'', called the ''k''th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order ''k'' of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial. Taylor's theorem is named after the mathematician Brook Taylor, who stated a version of it in 1715, although an earlier version of the result was already mentioned in 1671 by James Gregory. Taylor's theorem is taught in introductory-level calculus courses and is one of the central elementary tools in mathematical analysis. It gives simple arithmetic formula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Polynomials
In mathematics, the Bernoulli polynomials, named after Jacob Bernoulli, combine the Bernoulli numbers and binomial coefficients. They are used for series expansion of functions, and with the Euler–MacLaurin formula. These polynomials occur in the study of many special functions and, in particular, the Riemann zeta function and the Hurwitz zeta function. They are an Appell sequence (i.e. a Sheffer sequence for the ordinary derivative operator). For the Bernoulli polynomials, the number of crossings of the ''x''-axis in the unit interval does not go up with the degree. In the limit of large degree, they approach, when appropriately scaled, the sine and cosine functions. A similar set of polynomials, based on a generating function, is the family of Euler polynomials. Representations The Bernoulli polynomials ''B''''n'' can be defined by a generating function. They also admit a variety of derived representations. Generating functions The generating function for the Bernoulli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrand
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), and For example, the absolute value of 3 and the absolute value of −3 is The absolute value of a number may be thought of as its distance from zero. Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts. Terminology and notation In 1806, Jean-Robert Argand introduced the term ''module'', meaning ''unit of measure'' in French, specifically for the ''complex'' absolute value,Oxford English Dictionary, Draft Revision, June 2008 an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clausen Function
In mathematics, the Clausen function, introduced by , is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often referred to as ''the'' Clausen function, despite being but one of a class of many – is given by the integral: :\operatorname_2(\varphi)=-\int_0^\varphi \log\left, 2\sin\frac \\, dx: In the range 0 :\operatorname_2\left(-\frac+2m\pi \right) =-1.01494160 \ldots The following properties are immediate consequences of the series definition: :\operatorname_2(\theta+2m\pi) = \operatorname_2(\theta) :\operatorname_2(-\theta) = -\operatorname_2(\theta) See . General definition More generally, one defines the two generalized Clausen fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann Kinkelin
Hermann Kinkelin (11 November 1832 – 1 January 1913) was a Swiss mathematician and politician. Life His family came from Lindau on Lake Constance. He studied at the Universities of Zurich, Lausanne, and Munich. In 1865 he became professor of mathematics at the University of Basel, where until his retirement in 1908, the full burden of teaching of mathematics was his responsibility. In 1867 he was naturalized in Basel. He was also a statistician, he founded the Swiss Statistical Society and the Statistical-economic society in Basel and led the 1870 and 1880 Federal census in Basel. Kinkelin's works dealt with the gamma function, infinite series, and solid geometry In mathematics, solid geometry or stereometry is the traditional name for the geometry of Three-dimensional space, three-dimensional, Euclidean spaces (i.e., 3D geometry). Stereometry deals with the measurements of volumes of various solid fig ... of the axonometric. Kinkelin produced more than 60 publications i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Formula
In mathematics, a reflection formula or reflection relation for a function ''f'' is a relationship between ''f''(''a'' − ''x'') and ''f''(''x''). It is a special case of a functional equation, and it is very common in the literature to use the term "functional equation" when "reflection formula" is meant. Reflection formulas are useful for numerical computation of special functions. In effect, an approximation that has greater accuracy or only converges on one side of a reflection point (typically in the positive half of the complex plane) can be employed for all arguments. Known formulae The even and odd functions satisfy by definition simple reflection relations around ''a'' = 0. For all even functions, :f(-x) = f(x), and for all odd functions, :f(-x) = -f(x). A famous relationship is Euler's reflection formula :\Gamma(z)\Gamma(1-z) = \frac, \qquad z \not\in \mathbb Z for the gamma function \Gamma(z), due to Leonhard Euler. There is also a reflect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
