|
Multilinear Subspace Learning
Multilinear subspace learning is an approach to dimensionality reduction.M. A. O. Vasilescu, D. Terzopoulos (2003"Multilinear Subspace Analysis of Image Ensembles" "Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03), Madison, WI, June, 2003"M. A. O. Vasilescu, D. Terzopoulos (2002"Multilinear Analysis of Image Ensembles: TensorFaces" Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark, May, 2002M. A. O. Vasilescu,(2002"Human Motion Signatures: Analysis, Synthesis, Recognition" "Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 3, Quebec City, Canada, Aug, 2002, 456–460." Dimension reduction, Dimensionality reduction can be performed on a data tensor that contains a collection of observations have been vectorized, or observations that are treated as matrices and concatenated into a data tensor.X. He, D. Cai, P. NiyogiTensor subspace analysis in: Advances in Neural Information Proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
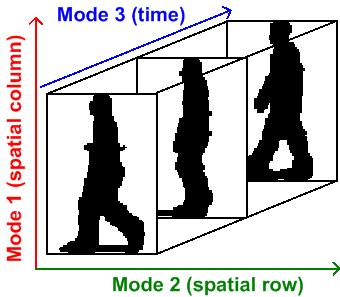
Video Represented As A Third-order Tensor
Video is an electronic medium for the recording, copying, playback, broadcasting, and display of moving visual media. Video was first developed for mechanical television systems, which were quickly replaced by cathode-ray tube (CRT) systems which, in turn, were replaced by flat panel displays of several types. Video systems vary in display resolution, aspect ratio, refresh rate, color capabilities and other qualities. Analog and digital variants exist and can be carried on a variety of media, including radio broadcast, magnetic tape, optical discs, computer files, and network streaming. History Analog video Video technology was first developed for mechanical television systems, which were quickly replaced by cathode-ray tube (CRT) television systems, but several new technologies for video display devices have since been invented. Video was originally exclusively a live technology. Charles Ginsburg led an Ampex research team developing one of the first practica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IEEE Conference On Computer Vision And Pattern Recognition
The Conference on Computer Vision and Pattern Recognition (CVPR) is an annual conference on computer vision and pattern recognition, which is regarded as one of the most important conferences in its field. According to Google Scholar Metrics (2022), it is the highest impact computing venue. Affiliations CVPR was first held in Washington DC in 1983 by Takeo Kanade and Dana Ballard (previously the conference was named Pattern Recognition and Image Processing). From 1985 to 2010 it was sponsored by the IEEE Computer Society. In 2011 it was also co-sponsored by University of Colorado Colorado Springs. Since 2012 it has been co-sponsored by the IEEE Computer Society and the Computer Vision Foundation, which provides open access to the conference papers. Scope CVPR considers a wide range of topics related to computer vision and pattern recognition—basically any topic that is extracting structures or answers from images or video or applying mathematical methods to data to extract or r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilinear Algebra
Multilinear algebra is a subfield of mathematics that extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of ''p''-vectors and multivectors with Grassmann algebras. Origin In a vector space of dimension ''n'', normally only vectors are used. However, according to Hermann Grassmann and others, this presumption misses the complexity of considering the structures of pairs, triplets, and general multi-vectors. With several combinatorial possibilities, the space of multi-vectors has 2''n'' dimensions. The abstract formulation of the determinant is the most immediate application. Multilinear algebra also has applications in the mechanical study of material response to stress and strain with various moduli of elasticity. This practical reference led to the use of the word tensor, to describe the elements of the multilinear space. The extra structure in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sandia National Laboratories
Sandia National Laboratories (SNL), also known as Sandia, is one of three research and development laboratories of the United States Department of Energy's National Nuclear Security Administration (NNSA). Headquartered in Kirtland Air Force Base in Albuquerque, New Mexico, it has a second principal facility next to Lawrence Livermore National Laboratory in California and a test facility in Waimea, Kauai, Hawaii. Sandia is owned by the U.S. federal government but privately managed and operated by National Technology and Engineering Solutions of Sandia, a wholly owned subsidiary of Honeywell International. Established in 1949, SNL is a "multimission laboratory" with the primary goal of advancing U.S. national security by developing various science-based technologies. Its work spans roughly 70 areas of activity, including nuclear deterrence, arms control, nonproliferation, hazardous waste disposal, and climate change. Sandia hosts a wide variety of research initiatives, incl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PARAFAC
In multilinear algebra, the tensor rank decomposition or the rank-R decomposition of a tensor is the decomposition of a tensor in terms of a sum of minimum R rank-1 tensors. This is an open problem. Canonical polyadic decomposition (CPD) is a variant of the rank decomposition which computes the best fitting K rank-1 terms for a user specified K. The CP decomposition has found some applications in linguistics and chemometrics. The CP rank was introduced by Frank Lauren Hitchcock in 1927 and later rediscovered several times, notably in psychometrics. The CP decomposition is referred to as CANDECOMP, PARAFAC, or CANDECOMP/PARAFAC (CP). Another popular generalization of the matrix SVD known as the higher-order singular value decomposition computes orthonormal mode matrices and has found applications in econometrics, signal processing, computer vision, computer graphics, psychometrics. Notation A scalar variable is denoted by lower case italic letters, a and an upper bound sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CP Decomposition
In multilinear algebra, the tensor rank decomposition or the rank-R decomposition of a tensor is the decomposition of a tensor in terms of a sum of minimum R rank-1 tensors. This is an open problem. Canonical polyadic decomposition (CPD) is a variant of the rank decomposition which computes the best fitting K rank-1 terms for a user specified K. The CP decomposition has found some applications in linguistics and chemometrics. The CP rank was introduced by Frank Lauren Hitchcock in 1927 and later rediscovered several times, notably in psychometrics. The CP decomposition is referred to as CANDECOMP, PARAFAC, or CANDECOMP/PARAFAC (CP). Another popular generalization of the matrix SVD known as the higher-order singular value decomposition computes orthonormal mode matrices and has found applications in econometrics, signal processing, computer vision, computer graphics, psychometrics. Notation A scalar variable is denoted by lower case italic letters, a and an upper bound scalar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Psychometrika
''Psychometrika'' is the official journal of the Psychometric Society, a professional body devoted to psychometrics and quantitative psychology. The journal covers quantitative methods for measurement and evaluation of human behavior, including statistical methods and other mathematical techniques. Past editors include Marion Richardson, Dorothy Adkins, Norman Cliff, and Willem J. Heiser. According to ''Journal Citation Reports'', the journal had a 2019 impact factor of 1.959. History In 1935 LL Thurstone, EL Thorndike and JP Guilford founded ''Psychometrika'' and also the Psychometric Society. Editors-in-chief The complete list of editor-in-chief of Psychometrika can be found at: https://www.psychometricsociety.org/content/past-psychometrika-editors The following is a subset of persons who have been editor-in-chief of Psychometrika: * Paul Horst * Albert K. Kurtz * Dorothy Adkins * Norman Cliff * Roger Millsap * Shizuhiko Nishisato * Willem J. Heiser * Irini Moustaki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tucker Decomposition
In mathematics, Tucker decomposition decomposes a tensor into a set of matrices and one small core tensor. It is named after Ledyard R. Tucker although it goes back to Hitchcock in 1927. Initially described as a three-mode extension of factor analysis and principal component analysis it may actually be generalized to higher mode analysis, which is also called higher-order singular value decomposition (HOSVD). It may be regarded as a more flexible PARAFAC (parallel factor analysis) model. In PARAFAC the core tensor is restricted to be "diagonal". In practice, Tucker decomposition is used as a modelling tool. For instance, it is used to model three-way (or higher way) data by means of relatively small numbers of components for each of the three or more modes, and the components are linked to each other by a three- (or higher-) way core array. The model parameters are estimated in such a way that, given fixed numbers of components, the modelled data optimally resemble the actual da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Higher-order Singular Value Decomposition
In multilinear algebra, the higher-order singular value decomposition (HOSVD) of a tensor is a specific orthogonal Tucker decomposition. It may be regarded as one generalization of the matrix singular value decomposition. It has applications in computer vision, computer graphics, machine learning, scientific computing, and signal processing. Some aspects can be traced as far back as F. L. Hitchcock in 1928, but it was L. R. Tucker who developed for third-order tensors the general Tucker decomposition in the 1960s, further advocated by L. De Lathauwer ''et al.'' in their Multilinear SVD work that employs the power method, and advocated by Vasilescu and Terzopoulos that developed M-mode SVD. The term HOSVD was coined by Lieven DeLathauwer, but the algorithm referred to commonly in the literature as the HOSVD and attributed to either Tucker or DeLathauwer was developed by Vasilescu and Terzopoulos.M. A. O. Vasilescu, D. Terzopoulos (2002) with the name M-mode SVD. It is a particul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Correlation Analysis
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X''''n'') and ''Y'' = (''Y''1, ..., ''Y''''m'') of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of ''X'' and ''Y'' which have maximum correlation with each other. T. R. Knapp notes that "virtually all of the commonly encountered parametric tests of significance can be treated as special cases of canonical-correlation analysis, which is the general procedure for investigating the relationships between two sets of variables." The method was first introduced by Harold Hotelling in 1936, although in the context of angles between flats the mathematical concept was published by Jordan in 1875. Definition Given two column vectors X = (x_1, \dots, x_n)^T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Component Analysis
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents. This is done by assuming that at most one subcomponent is Gaussian and that the subcomponents are statistically independent from each other. ICA is a special case of blind source separation. A common example application is the "cocktail party problem" of listening in on one person's speech in a noisy room. Introduction Independent component analysis attempts to decompose a multivariate signal into independent non-Gaussian signals. As an example, sound is usually a signal that is composed of the numerical addition, at each time t, of signals from several sources. The question then is whether it is possible to separate these contributing sources from the observed total signal. When the statistical independence assumption is correct, blind ICA separation of a mixed signal gives very good results. It is also used for signals that are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilinear Independent Component Analysis , a field of mathematics
{{mathdab ...
Multilinear may refer to: * Multilinear form, a type of mathematical function from a vector space to the underlying field * Multilinear map, a type of mathematical function between vector spaces * Multilinear algebra Multilinear algebra is a subfield of mathematics that extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of ''p' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
