|
Just Tuning
In music, just intonation or pure intonation is the Musical tuning, tuning of musical Interval (music), intervals as Natural number, whole number ratios (such as 3:2 or 4:3) of Frequency, frequencies. An interval (music), interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series (music), harmonic series of an implied fundamental frequency, fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth (music), fourth. In Western musical practice, instruments are rarely tuned using only pure intervals—the desire for different keys to have identical intervals in Western music makes this impractical. Some instruments of fixed pitch, such as el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series Klang
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and wind instrum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meantone Temperament
Meantone temperament is a musical temperament, that is a tuning system, obtained by narrowing the fifths so that their ratio is slightly less than 3:2 (making them ''narrower'' than a perfect fifth), in order to push the thirds closer to pure. Meantone temperaments are constructed the same way as Pythagorean tuning, as a stack of equal fifths, but it is a ''temperament'' in that the fifths are not pure. Notable meantone temperaments Equal temperament, obtained by making all semitones the same size, each equal to one-twelfth of an octave (with ratio the 12th root of 2 to one (:1), narrows the fifths by about 2 cents or 1/12 of a Pythagorean comma, and produces thirds that are only slightly better than in Pythagorean tuning. Equal temperament is roughly the same as 1/11 comma meantone tuning. Quarter-comma meantone, which tempers the fifths by 1/4 of a syntonic comma, is the best known type of meantone temperament, and the term ''meantone temperament'' is often used to refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
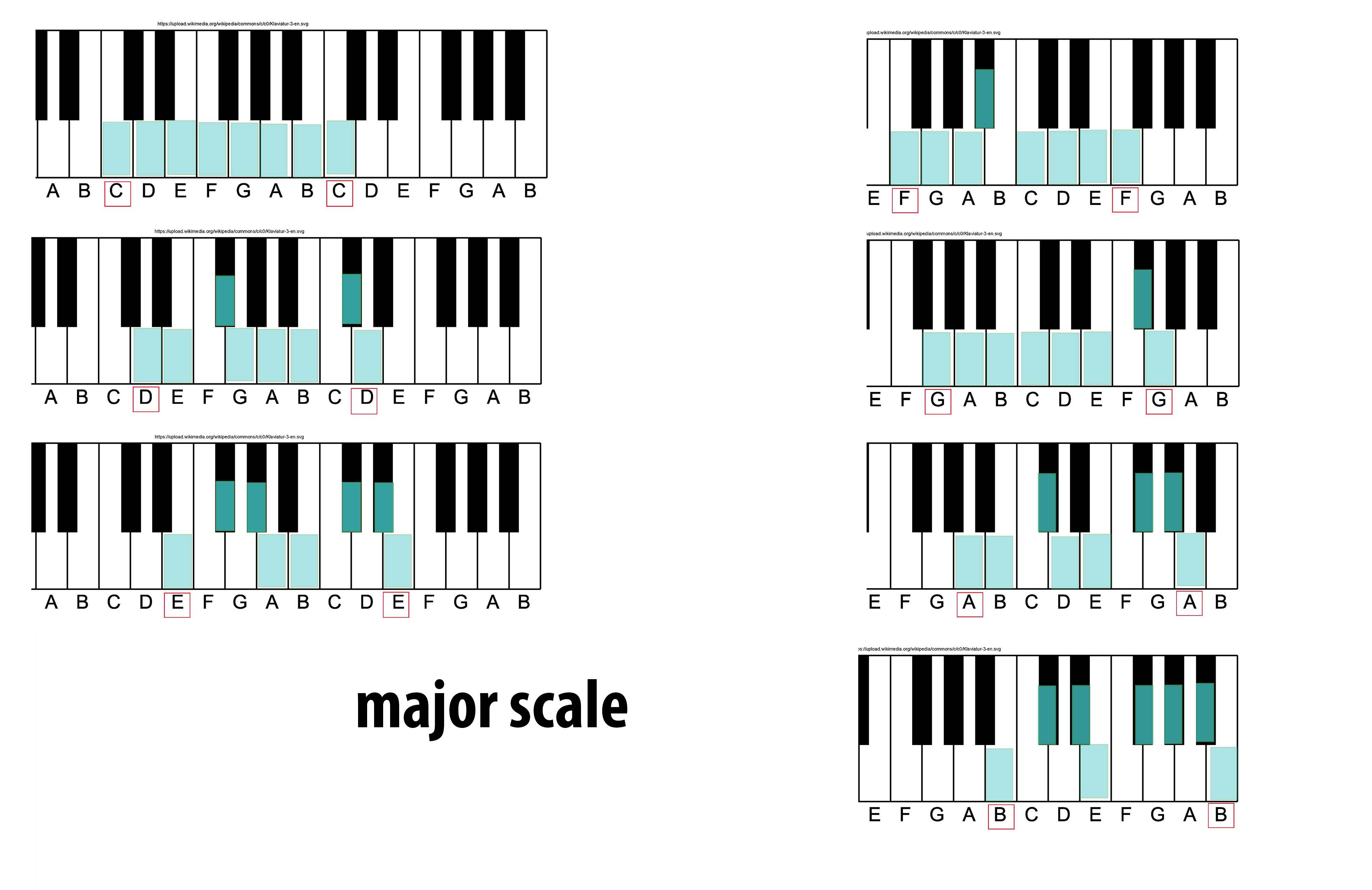
Major Scale
The major scale (or Ionian mode) is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note (from Latin "octavus", the eighth). The simplest major scale to write is C major, the only major scale not requiring sharps or flats: The major scale had a central importance in Western music, particularly in the common practice period and in popular music. In Carnatic music, it is known as '' Sankarabharanam''. In Hindustani classical music, it is known as '' Bilaval''. Structure A major scale is a diatonic scale. The sequence of intervals between the notes of a major scale is: : whole, whole, half, whole, whole, whole, half where "whole" stands for a whole tone (a red u-shaped curve in the figure), and "half" stands for a semitone (a red angled line in the figu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phrygian Mode
The Phrygian mode (pronounced ) can refer to three different musical modes: the ancient Greek ''tonos'' or ''harmonia,'' sometimes called Phrygian, formed on a particular set of octave species or scales; the Medieval Phrygian mode, and the modern conception of the Phrygian mode as a diatonic scale, based on the latter. Ancient Greek Phrygian The octave species (scale) underlying the ancient-Greek Phrygian ''tonos'' (in its diatonic genus) corresponds to the medieval and modern Dorian mode. The terminology is based on the '' Elements'' by Aristoxenos (fl. c. 335 BC), a disciple of Aristotle. The Phrygian ''tonos'' or ''harmonia'' is named after the ancient kingdom of Phrygia in Anatolia. In Greek music theory, the ''harmonia'' given this name was based on a ''tonos'', in turn based on a scale or octave species built from a tetrachord which, in its diatonic genus, consisted of a series of rising intervals of a whole tone, followed by a semitone, followed by a whole tone. : In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importance to later Byzantine, Islamic, and Western European science. The first is the astronomical treatise now known as the '' Almagest'', although it was originally entitled the ''Mathēmatikē Syntaxis'' or ''Mathematical Treatise'', and later known as ''The Greatest Treatise''. The second is the ''Geography'', which is a thorough discussion on maps and the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. This is sometimes known as the ''Apotelesmatika'' (lit. "On the Effects") but more commonly known as the '' Tetrábiblos'', from the Koine Greek meaning "Four Books", or by its Latin equivalent ''Quadrip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music & Letters
''Music & Letters'' is an academic journal published quarterly by Oxford University Press with a focus on musicology. The journal sponsors the Music & Letters Trust, twice-yearly cash awards of variable amounts to support research in the music field. A. H. Fox Strangways established the journal in 1920 and served as editor-in-chief until 1937. Eric Blom served as editor from 1937 to 1950 and again from 1954 to 1959. Other editors-in-chief have included Richard Capell, J.A. Westrup, Denis Arnold, Edward Olleson, Nigel Fortune, John Whenham John Whenham is an English musicologist and academic who specializes in early Italian baroque music. He earned both a Bachelor of Music and a Master of Music from the University of Nottingham, and a Doctor of Philosophy from the University of Oxfor ..., and Tim Carter. References External links * {{DEFAULTSORT:Music and Letters Music journals Oxford University Press academic journals Publications established in 1920 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eratosthenes
Eratosthenes of Cyrene (; grc-gre, Ἐρατοσθένης ; – ) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to what is now known as the study of geography, and he introduced some of the terminology still used today. He is best known for being the first person known to calculate the circumference of the Earth, which he did by using the extensive survey results he could access in his role at the Library; his calculation was remarkably accurate. He was also the first to calculate Earth's axial tilt, which has also proved to have remarkable accuracy. He created the first global projection of the world, incorporating parallels and meridians based on the available geographic knowledge of his era. Eratosthenes was the founder of scientific chronology; he used Egyptian and Persian records to estimate the dates of the main ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagoras
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samos, Samian, or simply ; in Ionian Greek; ) was an ancient Ionians, Ionian Ancient Greek philosophy, Greek philosopher and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, the Western philosophy, West in general. Knowledge of his life is clouded by legend, but he appears to have been the son of Mnesarchus, a gem-engraver on the island of Samos. Modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Crotone, Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, asceticism, ascetic lifestyle. This lifestyle entailed a number of dietary prohibitions, traditionally said to have included vegetarianism, although m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12-tet Scale Compared To Just In The Chromatic Circle
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the |
Comma (music)
In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word ''comma'' used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning system, and another F tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B and A are both approximated by the same inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.jpg)



