|
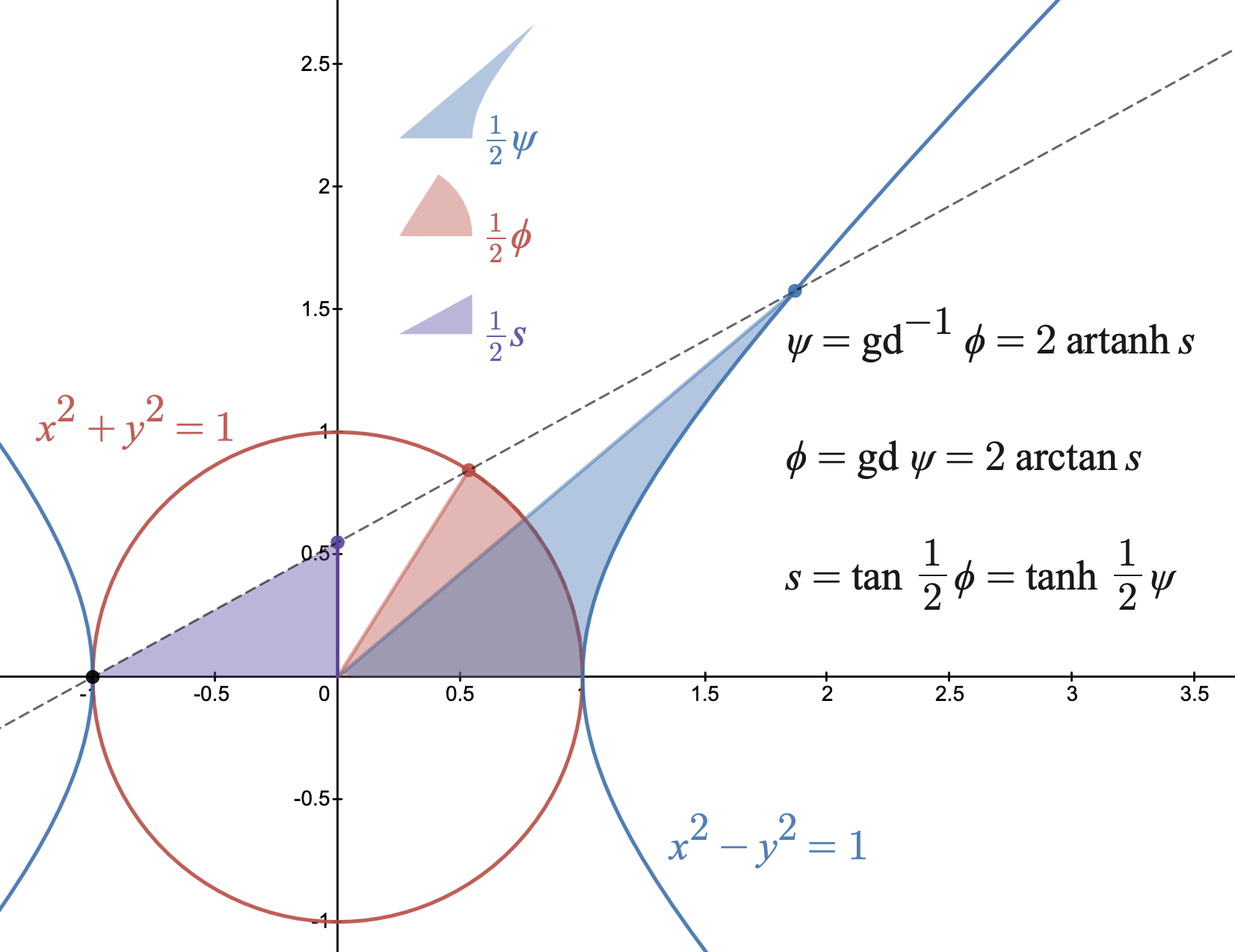
Hyperbolic Substitution
In mathematics, trigonometric substitution is the replacement of trigonometric functions for other expressions. In calculus, trigonometric substitution is a technique for evaluating integrals. Moreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration. Case I: Integrands containing ''a''2 − ''x''2 Let x = a \sin \theta, and use the identity 1-\sin^2 \theta = \cos^2 \theta. Examples of Case I Example 1 In the integral :\int\frac, we may use :x=a\sin \theta,\quad dx=a\cos\theta\, d\theta, \quad \theta=\arcsin\frac. Then, :\begin \int\frac &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \int d\theta \\ pt &= \theta + C \\ pt &= \arcsin\frac+C. \end The above step requires that a > 0 and \cos \theta > 0. We c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Of Secant Cubed
The integral of secant cubed is a frequent and challenging indefinite integral of elementary calculus: :\begin \int \sec^3 x \, dx &= \tfrac12\sec x \tan x + \tfrac12 \int \sec x\, dx + C \\ mu&= \tfrac12(\sec x \tan x + \ln \left, \sec x + \tan x\) + C \\ mu&= \tfrac12(\sec x \tan x + \operatorname^ x) + C, \qquad , x, < \tfrac12\pi \end where is the inverse , the . There are a number of reasons why this particular antiderivative is worthy of special attention: * The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simpl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Substitution
Euler substitution is a method for evaluating integrals of the form \int R(x, \sqrt) \, dx, where R is a rational function of x and \sqrt. In such cases, the integrand can be changed to a rational function by using the substitutions of Euler. Euler's first substitution The first substitution of Euler is used when a > 0. We substitute \sqrt = \pm x\sqrt + t and solve the resulting expression for x. We have that x = \frac and that the dx term is expressible rationally in t. In this substitution, either the positive sign or the negative sign can be chosen. Euler's second substitution If c > 0, we take \sqrt = xt \pm \sqrt. We solve for x similarly as above and find x = \frac. Again, either the positive or the negative sign can be chosen. Euler's third substitution If the polynomial ax^2 + bx + c has real roots \alpha and \beta, we may choose \sqrt = \sqrt = (x - \alpha)t. This yields x = \frac, and as in the preceding cases, we can express the entire integrand rationally i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards". Substitution for a single variable Introduction Before stating the result rigorously, consider a simple case using indefinite integrals. Compute \textstyle\int(2x^3+1)^7(x^2)\,dx. Set u=2x^3+1. This means \textstyle\frac=6x^2, or in differential form, du=6x^2\,dx. Now :\int(2x^3 +1)^7(x^2)\,dx = \frac\int\underbrace_\underbrace_=\frac\int u^\,du=\frac\left(\fracu^\right)+C=\frac(2x^3+1)^+C, where C is an arbitrary constant of integration. This procedure is frequently used, but not all integrals are of a form that permits its use. In any event, the result should be verified by differentiating and comparing to the original integrand. :\frac\left frac(2x^3+1)^+C\right\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 328 from which are derived: * hyperbolic tangent "" (), * hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Half-angle Formulas
In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half an angle is the stereographic projection of the circle onto a line. Among these formulas are the following: : \begin \tan \tfrac12( \eta \pm \theta) &= \frac = \frac = -\frac, \\[10pt] \tan \tfrac12 \theta &= \frac = \frac = \frac, & & (\eta = 0) \\[10pt] \tan \tfrac12 \theta &= \frac = \frac = \csc\theta-\cot\theta, & & (\eta = 0) \\[10pt] \tan \tfrac12 \big(\theta \pm \tfrac12\pi \big) &= \frac = \sec\theta \pm \tan\theta = \frac, & & \big(\eta = \tfrac12\pi \big) \\[10pt] \tan \tfrac12 \big(\theta \pm \tfrac12\pi \big) &= \frac = \frac = \frac, & & \big(\eta = \tfrac12\pi \big) \\[10pt] \frac &= \pm\sqrt \\[10pt] \tan \tfrac12 \theta &= \pm \sqrt \\[10pt] \end From these one can derive identities expressing the sine, cosine, and tangent as functions of tangents of half-angles: : \begin \sin \alpha & = \frac \\[7pt] \cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfrac x2. This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is: \int f(\sin x, \cos x)\, dx =\int f \frac. The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to evaluate the integral \int dx / (a + b\cos x) in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name. It is known in Russia as the universal trigonometric substitution, and also known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Of The Secant Function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities, : \int \sec \theta \, d\theta = \begin \dfrac12 \ln \left, \dfrac\ + C \\ 5pt\ln\left, \sec\theta + \tan\theta\ + C \\ 5pt\ln\left, \tan\left(\dfrac + \dfrac\right) \ + C\\ 5pt\end This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications. Proof that the different antiderivatives are equivalent Trigonometric forms : \int \sec \theta \, d\theta = \left\\text The second of these follows by first multiplying top and bottom of the interior fraction by . This gives in the denominator, and the result follows by moving the factor of into the logarithm as a square root. Leaving out the const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Fractions In Integration
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as a sum of a polynomial (possibly zero) and one or several fractions with a simpler denominator. The importance of the partial fraction decomposition lies in the fact that it provides algorithms for various computations with rational functions, including the explicit computation of antiderivatives, Taylor series expansions, inverse Z-transforms, and inverse Laplace transforms. The concept was discovered independently in 1702 by both Johann Bernoulli and Gottfried Leibniz. In symbols, the ''partial fraction decomposition'' of a rational fraction of the form \frac, where and are polynomials, is its expression as \frac=p(x) + \sum_j \frac where is a polynomial, and, for each , the denominator is a power of an irreducible polynomi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trig Sub Triangle 3
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the Babylonians, studied the ratios of the sides of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Parts
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation. The integration by parts formula states: \begin \int_a^b u(x) v'(x) \, dx & = \Big (x) v(x)\Biga^b - \int_a^b u'(x) v(x) \, dx\\ & = u(b) v(b) - u(a) v(a) - \int_a^b u'(x) v(x) \, dx. \end Or, letting u = u(x) and du = u'(x) \,dx while v = v(x) and dv = v'(x) \, dx, the formula can be written more compactly: \int u \, dv \ =\ uv - \int v \, du. Mathematician Brook Taylor discovered integration by parts, first publishing the idea in 1715. More general formulations of integration by parts ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trig Sub Triangle 2
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the Babylonians, studied the ratios of the sides of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |