|
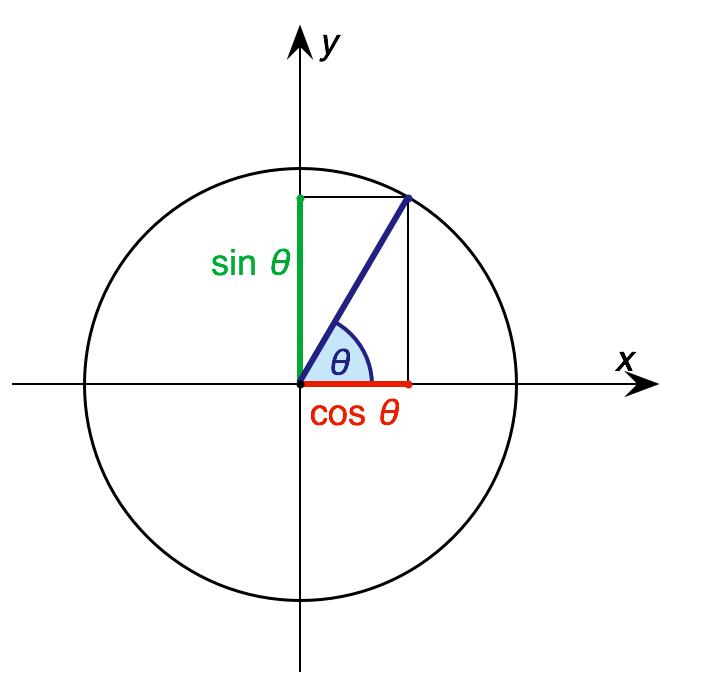
Tangent Half-angle Formulas
In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle.Mathematics'. United States, NAVEDTRA .e. NavalEducation and Training Program Management Support Activity, 1989. 6-19. Formulae The tangent of half an angle is the stereographic projection of the circle through the point at angle \pi radians onto the line through the angles \pm \frac. Tangent half-angle formulae include \begin \tan \tfrac12( \eta \pm \theta) &= \frac = \frac = -\frac\,, \end with simpler formulae when is known to be , , , or because and can be replaced by simple constants. In the reverse direction, the formulae include \begin \sin \alpha & = \frac \\ pt\cos \alpha & = \frac \\ pt\tan \alpha & = \frac\,. \end Proofs Algebraic proofs Using the angle addition and subtraction formulae for both the sine and cosine one obtains \begin \sin (a+b) + \sin (a-b) &= 2 \sin a \cos b \\ 5mu\cos (a+b) + \cos (a-b) & = 2 \cos a \cos b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planetmath
PlanetMath is a free content, free, collaborative, mathematics online encyclopedia. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org, Ltd". PlanetMath was started when the popular free online mathematics encyclopedia MathWorld was temporarily taken offline for 12 months by a court injunction as a result of the CRC Press lawsuit against the Wolfram Research company and its employee (and MathWorld's author) Eric Weisstein. Materials The main PlanetMath focus is on encyclopedia, encyclopedic entries. It formerly operated a self-hosted forum, but now encourages discussion via Gitter. An all-inclusive PlanetMath ''Free Encyclopedia'' book of 2,300 pages is available for the encyclopedia contents up to 2006 as a free download PDF file. Content development model PlanetMath implements a specific content creation system called ''authority model''. An author who starts a ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Half-side Formula
In spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles. For a triangle \triangle ABC on a sphere, the half-side formula is. \begin \tan \tfrac12 a &= \sqrt \end where are the angular lengths (measure of central angle, arc lengths normalized to a sphere of unit radius) of the sides opposite angles respectively, and S = \tfrac12 (A+B+ C) is half the sum of the angles. Two more formulas can be obtained for b and c by permuting the labels A, B, C. The polar dual relationship for a spherical triangle is the ''half-angle formula'', \begin \tan \tfrac12 A &= \sqrt \end where semiperimeter s = \tfrac12 (a + b + c) is half the sum of the sides. Again, two more formulas can be obtained by permuting the labels A, B, C. Half-tangent variant The same relationships can be written as rational equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Trigonometric Identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle. These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity. Pythagorean identities The basic relationship between the sine and cosine is given by the Pythagorean identity: \sin^2\theta + \cos^2\theta = 1, where \sin^2 \theta means ^2 and \cos^2 \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Extension
In mathematics, particularly in algebra, a field extension is a pair of fields K \subseteq L, such that the operations of ''K'' are those of ''L'' restricted to ''K''. In this case, ''L'' is an extension field of ''K'' and ''K'' is a subfield of ''L''. For example, under the usual notions of addition and multiplication, the complex numbers are an extension field of the real numbers; the real numbers are a subfield of the complex numbers. Field extensions are fundamental in algebraic number theory, and in the study of polynomial roots through Galois theory, and are widely used in algebraic geometry. Subfield A subfield K of a field L is a subset K\subseteq L that is a field with respect to the field operations inherited from L. Equivalently, a subfield is a subset that contains the multiplicative identity 1, and is closed under the operations of addition, subtraction, multiplication, and taking the inverse of a nonzero element of K. As , the latter definition implies K and L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heronian Triangle
In geometry, a Heronian triangle (or Heron triangle) is a triangle whose side lengths , , and and area are all positive integers. Heronian triangles are named after Heron of Alexandria, based on their relation to Heron's formula which Heron demonstrated with the example triangle of sides and area . Heron's formula implies that the Heronian triangles are exactly the positive integer solutions of the Diophantine equation :16\,A^2=(a+b+c)(a+b-c)(b+c-a)(c+a-b); that is, the side lengths and area of any Heronian triangle satisfy the equation, and any positive integer solution of the equation describes a Heronian triangle. If the three side lengths are setwise coprime (meaning that the greatest common divisor of all three sides is 1), the Heronian triangle is called ''primitive''. Triangles whose side lengths and areas are all rational numbers (positive rational solutions of the above equation) are sometimes also called ''Heronian triangles'' or ''rational triangles''; in this art ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similar (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipses can have different width to height ratios, two rectangles can have different length to breadth ratios, and two iso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
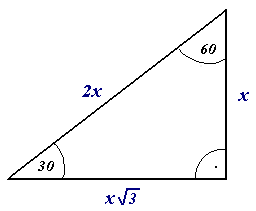
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior Angle
In geometry, an angle of a polygon is formed by two adjacent sides. For a simple polygon (non-self-intersecting), regardless of whether it is convex or non-convex, this angle is called an internal angle (or interior angle) if a point within the angle is in the interior of the polygon. A polygon has exactly one internal angle per vertex. If every internal angle of a simple polygon is less than a straight angle ( radians or 180°), then the polygon is called convex. In contrast, an external angle (also called a turning angle or exterior angle) is an angle formed by one side of a simple polygon and a line extended from an adjacent side.Posamentier, Alfred S., and Lehmann, Ingmar. ''The Secrets of Triangles'', Prometheus Books, 2012. Properties * The sum of the internal angle and the external angle on the same vertex is radians (180°). * The sum of all the internal angles of a simple polygon is radians or degrees, where is the number of sides. The formula can be prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Triangle
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A triangle whose side lengths are a Pythagorean triple is a right triangle and called a Pythagorean triangle. A primitive Pythagorean triple is one in which , and are coprime (that is, they have no common divisor larger than 1). For example, is a primitive Pythagorean triple whereas is not. Every Pythagorean triple can be scaled to a unique primitive Pythagorean triple by dividing by their greatest common divisor. Conversely, every Pythagorean triple can be obtained by multiplying the elements of a primitive Pythagorean triple by a positive integer (the same for the three elements). The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula a^2+b^2=c^2; thus, Pythagorean triples describe the three integer s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |