|
Complex Squaring Map
In mathematics, the complex squaring map, a polynomial mapping of degree two, is a simple and accessible demonstration of chaos in dynamical systems. It can be constructed by performing the following steps: # Choose any complex number on the unit circle whose argument (angle) is not a rational multiple of π, # Repeatedly square that number. This repetition (iteration) produces a sequence of complex numbers that can be described alone by their arguments. Any choice of starting angle that satisfies (1) above will produce an extremely complicated sequence of angles, that belies the simplicity of the steps. It can be shown that the sequence will be chaotic, i.e. it is sensitive to the detailed choice of starting angle. Chaos and the complex squaring map The informal reason why the iteration is chaotic is that the angle doubles on every iteration and doubling grows very quickly as the angle becomes ever larger, but angles which differ by multiples of 2π (radians) are identical. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
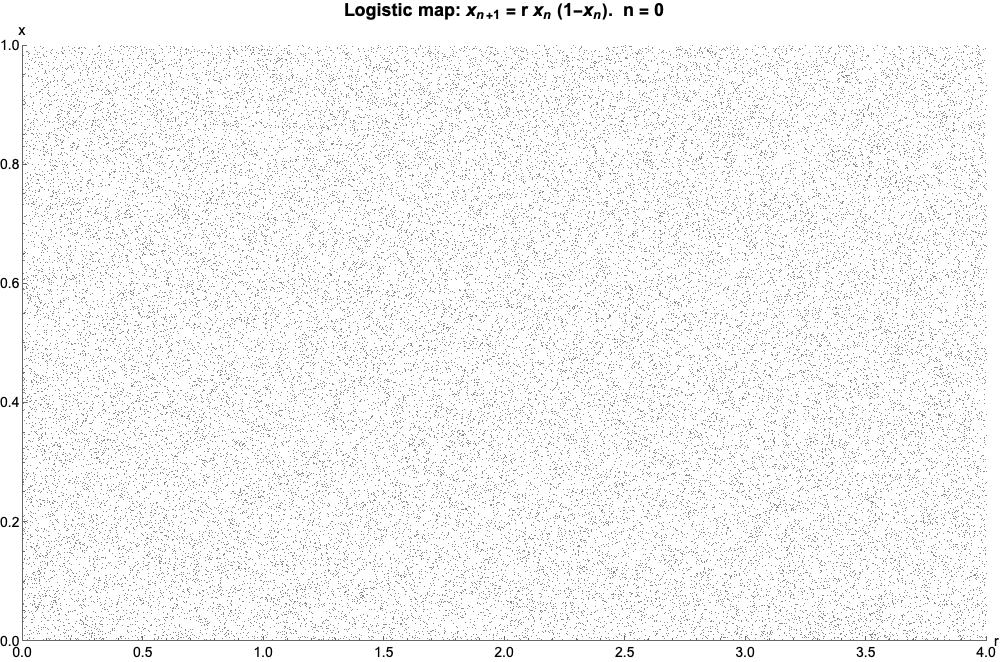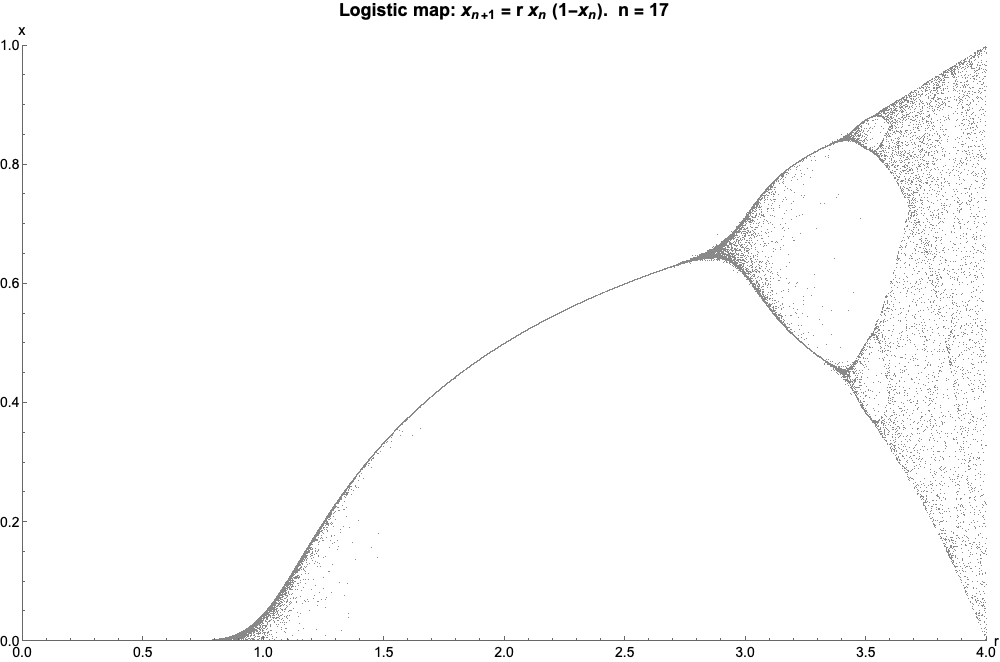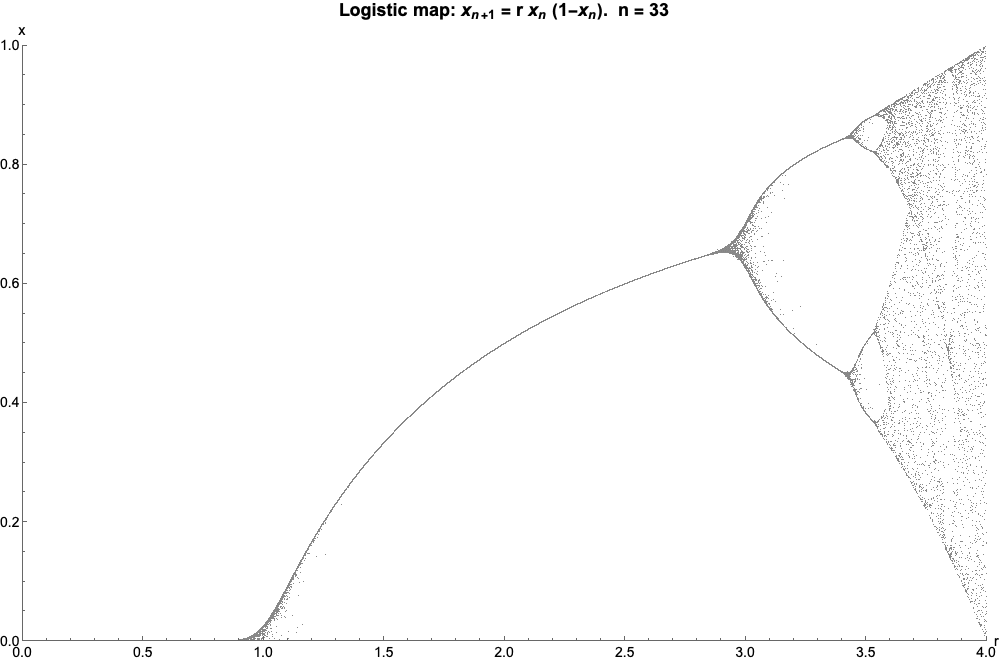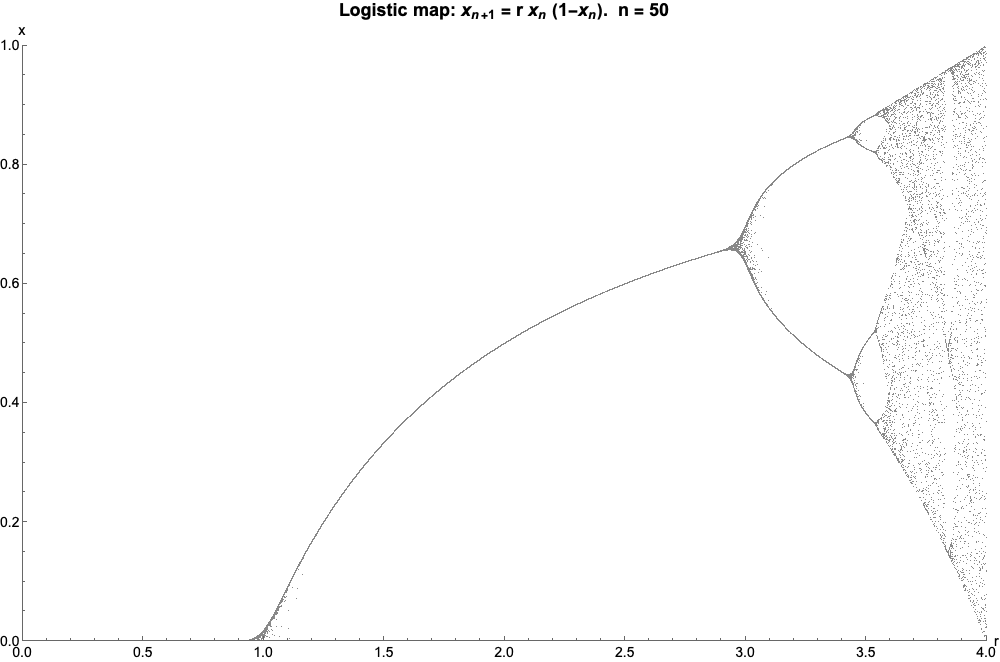
Logistic Map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written where is a number between zero and one, that represents the ratio of existing population to the maximum possible population. This nonlinear difference equation is intended to capture two effects: * ''reproduction'' where the population will increase at a rate proportional to the current population when the population size is small. * ''starvation'' (density-dependent mortality) where the growth rate will decrease at a rate proportional to the value obtained by taking the theoretical "carrying capacity" of the environment l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Base
In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal/denary system (the most common system in use today) the radix (base number) is ten, because it uses the ten digits from 0 through 9. In any standard positional numeral system, a number is conventionally written as with ''x'' as the string of digits and ''y'' as its base, although for base ten the subscript is usually assumed (and omitted, together with the pair of parentheses), as it is the most common way to express value. For example, (the decimal system is implied in the latter) and represents the number one hundred, while (100)2 (in the binary system with base 2) represents the number four. Etymology ''Radix'' is a Latin word for "root". ''Root'' can be considered a synonym for ''base,'' in the arithmetical sense. In numeral systems In the system with radix 13, for example, a string of digits such as 398 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called ''Cardinal number, cardinal numbers'', and numbers used for ordering are called ''Ordinal number, ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports Number (sports), jersey numbers). Some definitions, including the standard ISO/IEC 80000, ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Quadratic Map
A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers. Properties Quadratic polynomials have the following properties, regardless of the form: *It is a unicritical polynomial, i.e. it has one finite critical point in the complex plane, Dynamical plane consist of maximally 2 basins: basin of infinity and basin of finite critical point ( if finite critical point do not escapes) *It can be postcritically finite, i.e. the orbit of the critical point can be finite, because the critical point is periodic or preperiodic. * It is a unimodal function, * It is a rational function, * It is an entire function. Forms When the quadratic polynomial has only one variable (univariate), one can distinguish its four main forms: * The general form: f(x) = a_2 x^2 + a_1 x + a_0 where a_2 \ne 0 * The factored form used for the logistic map: f_r(x) = r x (1-x) * f_(x) = x^2 +\lambda x which has an indifferent fixed point with multiplier \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number : e^ = \cos x + i\sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus i sine"). The formula is still valid if is a complex number, and so some authors refer to the more general complex version as Euler's formula. Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes presented a geometrical ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit (dynamics)
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynamical system under a particular set of initial conditions, as the system evolves. As a phase space trajectory is uniquely determined for any given set of phase space coordinates, it is not possible for different orbits to intersect in phase space, therefore the set of all orbits of a dynamical system is a partition of the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems. For discrete-time dynamical systems, the orbits are sequences; for real dynamical systems, the orbits are curves; and for holomorphic dynamical systems, the orbits are Riemann surfaces. Definition Given a dynamical system (''T'', ''M'', Φ) with ''T'' a group, ''M'' a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Transformation
The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation) : T: , 1) \to [0, 1)^\infty : x \mapsto (x_0, x_1, x_2, \ldots) (where [0, 1)^\infty is the set of sequences from [0, 1)) produced by the rule : x_0 = x : \text n \ge 0,\ x_ = (2 x_n) \bmod 1. Equivalently, the dyadic transformation can also be defined as the iterated function map of the piecewise linear function : T(x)=\begin2x & 0 \le x < \frac \\2x-1 & \frac \le x < 1. \end The name ''bit shift map'' arises because, if the value of an iterate is written in notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero. The dyadic transform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be ''finite'', as in these examples, or ''infi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |