|
Complex Quadratic Map
A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers. Properties Quadratic polynomials have the following properties, regardless of the form: *It is a unicritical polynomial, i.e. it has one finite critical point in the complex plane, Dynamical plane consist of maximally 2 basins: basin of infinity and basin of finite critical point ( if finite critical point do not escapes) *It can be postcritically finite, i.e. the orbit of the critical point can be finite, because the critical point is periodic or preperiodic. * It is a unimodal function, * It is a rational function, * It is an entire function. Forms When the quadratic polynomial has only one variable (univariate), one can distinguish its four main forms: * The general form: f(x) = a_2 x^2 + a_1 x + a_0 where a_2 \ne 0 * The factored form used for the logistic map: f_r(x) = r x (1-x) * f_(x) = x^2 +\lambda x which has an indifferent fixed point with multiplier \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Polynomial
In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic". For example, a univariate (single-variable) quadratic function has the form :f(x)=ax^2+bx+c,\quad a \ne 0, where is its variable. The graph of a univariate quadratic function is a parabola, a curve that has an axis of symmetry parallel to the -axis. If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros of the corresponding quadratic function. The bivariate case in terms of variables and has the form : f(x,y) = a x^2 + bx y+ c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and the viscosities ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
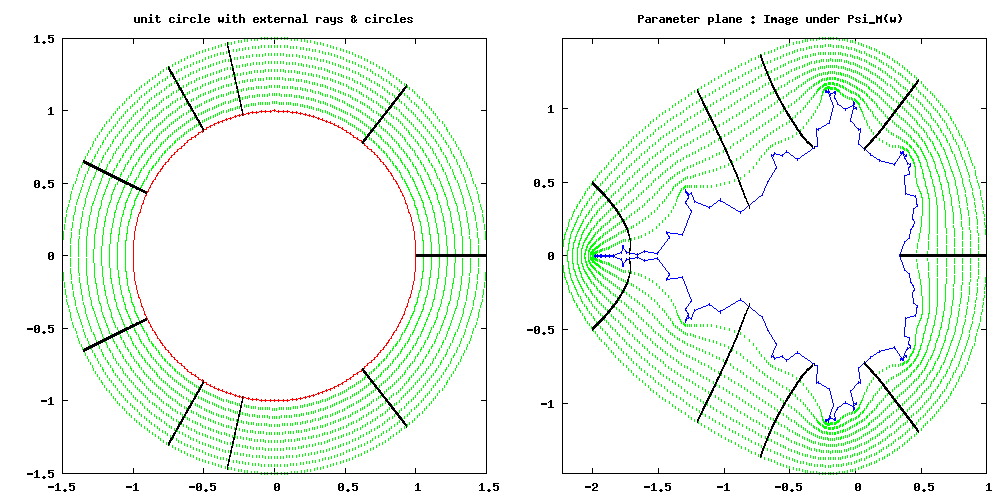
External Ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray. External rays are used in complex analysis, particularly in complex dynamics and geometric function theory. History External rays were introduced in Douady and Hubbard's study of the Mandelbrot set Types Criteria for classification : * plane : parameter or dynamic * map * bifurcation of dynamic rays * Stretching * landing plane External rays of (connected) Julia sets on dynamical plane are often called dynamic rays. External rays of the Mandelbrot set (and similar one-dimensional connectedness loci) on parameter plane are called parameter rays. bifurcation Dynamic ray can be: * bifurcated = branched = broken * smooth = unbranched = unbroken When the filled Julia set is connected, there are no branching external rays. When the Julia set is not connected then some external r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
External Ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray. External rays are used in complex analysis, particularly in complex dynamics and geometric function theory. History External rays were introduced in Douady and Hubbard's study of the Mandelbrot set Types Criteria for classification : * plane : parameter or dynamic * map * bifurcation of dynamic rays * Stretching * landing plane External rays of (connected) Julia sets on dynamical plane are often called dynamic rays. External rays of the Mandelbrot set (and similar one-dimensional connectedness loci) on parameter plane are called parameter rays. bifurcation Dynamic ray can be: * bifurcated = branched = broken * smooth = unbranched = unbroken When the filled Julia set is connected, there are no branching external rays. When the Julia set is not connected then some external r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterated Function
In mathematics, an iterated function is a function (that is, a function from some set to itself) which is obtained by composing another function with itself a certain number of times. The process of repeatedly applying the same function is called iteration. In this process, starting from some initial object, the result of applying a given function is fed again in the function as input, and this process is repeated. For example on the image on the right: :with the circle‑shaped symbol of function composition. Iterated functions are objects of study in computer science, fractals, dynamical systems, mathematics and renormalization group physics. Definition The formal definition of an iterated function on a set ''X'' follows. Let be a set and be a function. Defining as the ''n''-th iterate of (a notation introduced by Hans Heinrich Bürmann and John Frederick William Herschel), where ''n'' is a non-negative integer, by: f^0 ~ \stackrel ~ \operatorname_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Transformation
The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation) : T: , 1) \to [0, 1)^\infty : x \mapsto (x_0, x_1, x_2, \ldots) (where [0, 1)^\infty is the set of sequences from [0, 1)) produced by the rule : x_0 = x : \text n \ge 0,\ x_ = (2 x_n) \bmod 1. Equivalently, the dyadic transformation can also be defined as the iterated function map of the piecewise linear function : T(x)=\begin2x & 0 \le x < \frac \\2x-1 & \frac \le x < 1. \end The name ''bit shift map'' arises because, if the value of an iterate is written in notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero. The dyadic transform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fatou Set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic". The Julia set of a function is commonly denoted \operatorname(f), and the Fatou set is denoted \operatorname(f). These sets are named after the French mathematicians Gaston Julia and Pierre Fatou whose work began the study of complex dynamics during the early 20th century. Formal definition Let f(z) be a non-constant holomorphic function from the Riemann sphere o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julia Set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic". The Julia set of a function is commonly denoted \operatorname(f), and the Fatou set is denoted \operatorname(f). These sets are named after the French mathematicians Gaston Julia and Pierre Fatou whose work began the study of complex dynamics during the early 20th century. Formal definition Let f(z) be a non-constant holomorphic function from the Riemann sphere on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandelbrot Set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value. This set was first defined and drawn by Robert W. Brooks and Peter Matelski in 1978, as part of a study of Kleinian groups. Afterwards, in 1980, Benoit Mandelbrot obtained high-quality visualizations of the set while working at IBM's Thomas J. Watson Research Center in Yorktown Heights, New York. Images of the Mandelbrot set exhibit an elaborate and infinitely complicated boundary that reveals progressively ever-finer recursive detail at increasing magnifications; mathematically, one would say that the boundary of the Mandelbrot set is a ''fractal curve''. The "style" of this recursive detail depends on the region of the set boundary being examined. Mandelbrot set images may be created by sampling the complex numbers and testing, for each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Dynamics
Complex dynamics is the study of dynamical systems defined by Iterated function, iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions. Techniques *General **Montel's theorem **Poincaré metric **Schwarz lemma **Riemann mapping theorem **Carathéodory's theorem (conformal mapping) **Böttcher's equation *Combinatorics, Combinatorial ** Hubbard trees ** Spider algorithm ** Tuning **Lamination (topology), Laminations **Cantor function, Devil's Staircase algorithm (Cantor function) **Orbit portraits **Jean-Christophe Yoccoz, Yoccoz puzzles Parts * Holomorphic dynamics (dynamics of holomorphic functions) ** in one complex variable ** in several complex variables * Conformal dynamics unites holomorphic dynamics in one complex variable with differentiable dynamics in one real variable. See also *Arithmetic dynamics *Chaos theory *Complex analysis *Complex quadratic polynomial *Fatou set *Infinite co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Conjugation
In mathematics, two functions are said to be topologically conjugate if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy, and related-but-distinct of flows, are important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterative function can be determined, then that for a topologically conjugate function follows trivially. To illustrate this directly: suppose that f and g are iterated functions, and there exists a homeomorphism h such that :g = h^ \circ f \circ h, so that f and g are topologically conjugate. Then one must have :g^n = h^ \circ f^n \circ h, and so the iterated systems are topologically conjugate as well. Here, \circ denotes function composition. Definition f\colon X \to X, g\colon Y \to Y, and h\colon Y \to X are continuous functions on topological spaces, X and Y. f being topologically semiconjugate to g means, by definition, that h is a surjection such t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can be repre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |