|
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist with broad interests and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the " second great unification in physics" where the first one had been realised by Isaac Newton. With the publication of "A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society. His statement that "light and magnetism are affections of the same substance" is at page 499.) The unification of light ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edinburgh
Edinburgh ( ; gd, Dùn Èideann ) is the capital city of Scotland and one of its 32 Council areas of Scotland, council areas. Historically part of the county of Midlothian (interchangeably Edinburghshire before 1921), it is located in Lothian on the southern shore of the Firth of Forth. Edinburgh is Scotland's List of towns and cities in Scotland by population, second-most populous city, after Glasgow, and the List of cities in the United Kingdom, seventh-most populous city in the United Kingdom. Recognised as the capital of Scotland since at least the 15th century, Edinburgh is the seat of the Scottish Government, the Scottish Parliament and the Courts of Scotland, highest courts in Scotland. The city's Holyrood Palace, Palace of Holyroodhouse is the official residence of the Monarchy of the United Kingdom, British monarchy in Scotland. The city has long been a centre of education, particularly in the fields of medicine, Scots law, Scottish law, literature, philosophy, the sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betti's Theorem
Betti's theorem, also known as Maxwell–Betti reciprocal work theorem, discovered by Enrico Betti in 1872, states that for a linear elastic structure subject to two sets of forces i=1,...,n and , j=1,2,...,n, the work done by the set P through the displacements produced by the set Q is equal to the work done by the set Q through the displacements produced by the set P. This theorem has applications in structural engineering where it is used to define influence lines and derive the boundary element method. Betti's theorem is used in the design of compliant mechanisms by topology optimization approach. Proof Consider a solid body subjected to a pair of external force systems, referred to as F^P_i and F^Q_i. Consider that each force system causes a displacement field, with the displacements measured at the external force's point of application referred to as d^P_i and d^Q_i. When the F^P_i force system is applied to the structure, the balance between the work performed by the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Yield Criterion
The maximum distortion criterion (also von Mises yield criterion) states that yielding of a ductile material begins when the second invariant of deviatoric stress J_2 reaches a critical value. It is a part of plasticity theory that mostly applies to ductile materials, such as some metals. Prior to yield, material response can be assumed to be of a nonlinear elastic, viscoelastic, or linear elastic behavior. In materials science and engineering von Mises yield criterion is also formulated in terms of the von Mises stress or equivalent tensile stress, \sigma_\text. This is a scalar value of stress that can be computed from the Cauchy stress tensor. In this case, a material is said to start yielding when the von Mises stress reaches a value known as yield strength, \sigma_\text. The von Mises stress is used to predict yielding of materials under complex loading from the results of uniaxial tensile tests. The von Mises stress satisfies the property where two stress states with equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell Material
A Maxwell material is the most simple model viscoelastic material showing properties of a typical liquid. It shows viscous flow on the long timescale, but additional elastic resistance to fast deformations. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid. Definition The Maxwell model is represented by a purely viscous damper and a purely elastic spring connected in series, as shown in the diagram. In this configuration, under an applied axial stress, the total stress, \sigma_\mathrm and the total strain, \varepsilon_\mathrm can be defined as follows: :\sigma_\mathrm=\sigma_D = \sigma_S :\varepsilon_\mathrm=\varepsilon_D+\varepsilon_S where the subscript D indicates the stress–strain in the damper and the subscript S indicates the stress–strain in the spring. Taking the derivative of strain with respect to time, we obtain: :\frac = \frac + \frac = \frac + \frac \frac where ''E'' is the elastic modul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Theorem (geometry)
Maxwell's theorem is the following statement about triangles in the plane. The theorem is named after the physicist James Clerk Maxwell (1831–1879), who proved it in his work on reciprocal figures, which are of importance in statics Statics is the branch of classical mechanics that is concerned with the analysis of force and torque (also called moment) acting on physical systems that do not experience an acceleration (''a''=0), but rather, are in static equilibrium with t .... References * Daniel Pedoe: ''Geometry: A Comprehensive Course''. Dover, 1970, pp. 35–36, 114–115 * Daniel Pedoe: "On (what should be) a Well-Known Theorem in Geometry." ''The American Mathematical Monthly'', Vol. 74, No. 7 (August – September, 1967), pp. 839–841JSTOR *Dao Thanh Oai, Cao Mai Doai, Quang Trung, Kien Xuong, Thai Binh"Generalizations of some famous classical Euclidean geometry theorems."''International Journal of Computer Discovered Mathematics'', Vol. 1, No. 3, pp. 13–20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Theorem
In probability theory, Maxwell's theorem, named in honor of James Clerk Maxwell, states that if the probability distribution of a vector-valued random variable ''X'' = ( ''X''1, ..., ''X''''n'' )''T'' is the same as the distribution of ''GX'' for every ''n''×''n'' orthogonal matrix ''G'' and the components are independent, then the components ''X''1, ..., ''X''''n'' are normally distributed with expected value 0 and all have the same variance. This theorem is one of many characterizations of the normal distribution. Since a multiplication by an orthogonal matrix is a rotation, the theorem says that if the probability distribution of a random vector is unchanged by rotations and if the components are independent, then the components are identically distributed and normally distributed. In other words, the only rotationally invariant probability distributions on R''n'' that have independent components are multivariate normal distributions with expected value 0 and variance I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress Functions
In linear elasticity, the equations describing the deformation of an elastic body subject only to surface forces (or body forces that could be expressed as potentials) on the boundary are (using index notation) the equilibrium equation: :\sigma_=0\, where \sigma is the stress tensor, and the Beltrami-Michell compatibility equations: :\sigma_+\frac\sigma_=0 A general solution of these equations may be expressed in terms of the Beltrami stress tensor. Stress functions are derived as special cases of this Beltrami stress tensor which, although less general, sometimes will yield a more tractable method of solution for the elastic equations. Beltrami stress functions It can be shown that a complete solution to the equilibrium equations may be written as :\sigma=\nabla \times \Phi \times \nabla Using index notation: :\sigma_=\varepsilon_\varepsilon_\Phi_ : where \Phi_ is an arbitrary second-rank tensor field that is at least twice differentiable, and is known as the ''Beltr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell Speed Distribution
Maxwell may refer to: People * Maxwell (surname), including a list of people and fictional characters with the name ** James Clerk Maxwell, mathematician and physicist * Justice Maxwell (other) * Maxwell baronets, in the Baronetage of Nova Scotia * Maxwell (footballer, born 1979), Brazilian forward * Maxwell (footballer, born 1981), Brazilian left-back * Maxwell (footballer, born 1986), Brazilian striker * Maxwell (footballer, born 1989), Brazilian left-back * Maxwell (footballer, born 1995), Brazilian forward * Maxwell (musician) (born 1973), American R&B and neo-soul singer * Maxwell (rapper) (born 1993), German rapper, member of rap band 187 Strassenbande * Maxwell Jacob Friedman (born 1997) AEW Professional wrestler * Maxwell Silva (born 1953), Sri Lankan Sinhala Catholic cleric, Auxiliary Bishop of Colombo Places United States * Maxwell, California * Maxwell, Indiana * Maxwell, Iowa * Maxwell, Nebraska * Maxwell, New Mexico * Maxwell, Texas * Maxwell Ai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Discs
A color triangle is an arrangement of colors within a triangle, based on the additive combination of three primary colors at its corners. An additive color space defined by three primary colors has a chromaticity gamut that is a color triangle, when the amounts of the primaries are constrained to be nonnegative. Before the theory of additive color was proposed by Thomas Young and further developed by James Clerk Maxwell and Hermann von Helmholtz, triangles were also used to organize colors, for example around a system of red, yellow, and blue primary colors. After the development of the CIE system, color triangles were used as chromaticity diagrams, including briefly with the trilinear coordinates representing the chromaticity values. Since the sum of the three chromaticity values has a fixed value, it suffices to depict only two of the three values, using Cartesian co-ordinates. In the modern ''x,y'' diagram, the large triangle bounded by the imaginary prima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic Coupling
Kinematic coupling describes fixtures designed to exactly constrain the part in question, providing precision and certainty of location. A canonical example of a kinematic coupling consists of three radial v-grooves in one part that mate with three hemispheres in another part. Each hemisphere has two contact points for a total of six contact points, enough to constrain all six of the part's degrees of freedom. An alternative design consists of three hemispheres on one part that fit respectively into a tetrahedral dent, a v-groove, and a flat. Background Kinematic couplings arose from the need of precision coupling between structural interfaces that were meant to be routinely taken apart and put back together. Kelvin Coupling The Kelvin coupling is named after William Thompson (Lord Kelvin) who published the design in 1868–71. It consists of three spherical surfaces that rest on a concave tetrahedron, a V-groove pointing towards the tetrahedron and a flat plate. The tetrah ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
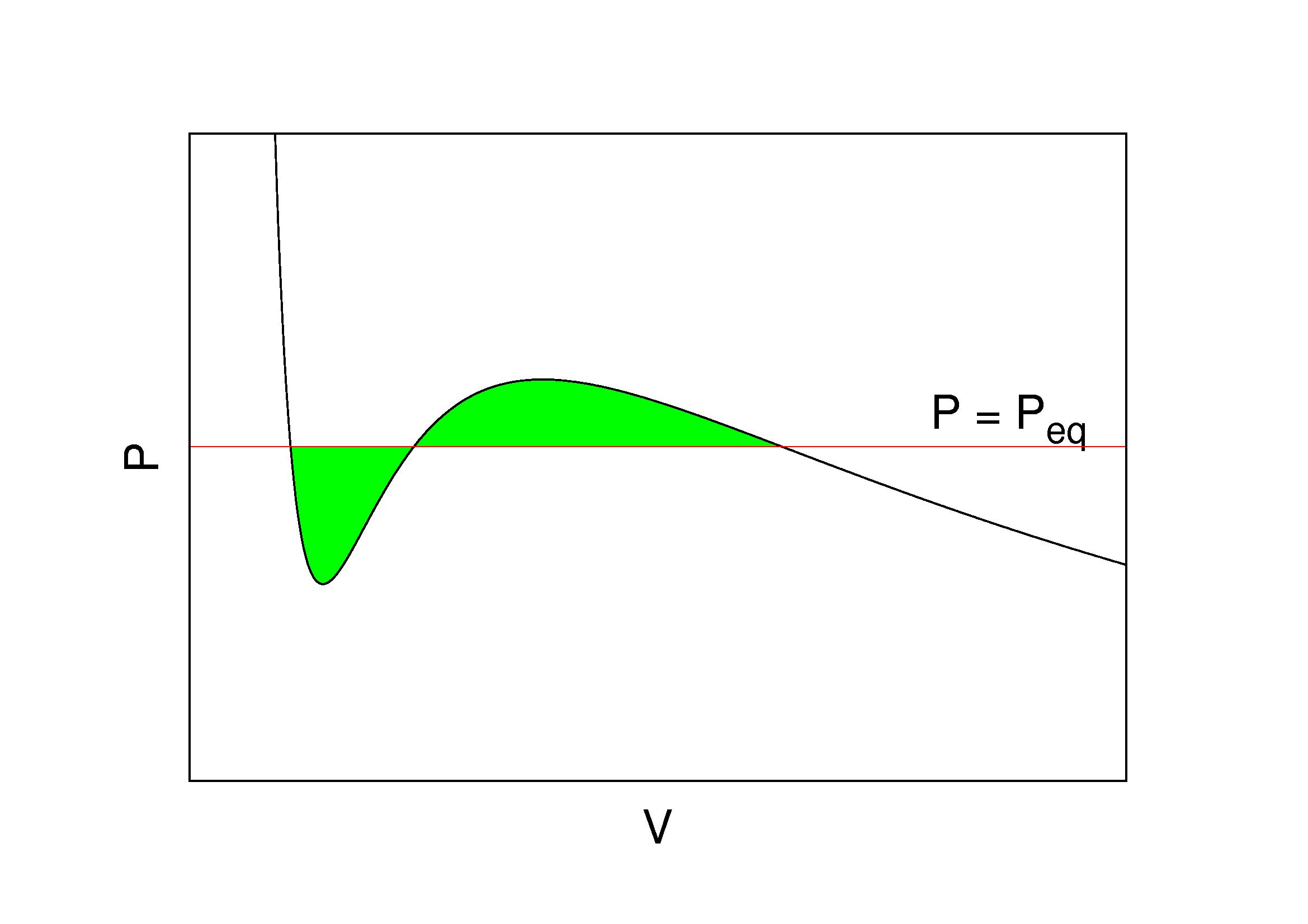
Maxwell Construction
In thermodynamic equilibrium, a necessary condition for stability is that pressure P does not increase with volume V. This basic consistency requirement—and similar ones for other ''conjugate'' pairs of variables—are sometimes violated in analytic models for first order phase transitions. The most famous case is the Van der Waals equation for real gases, see Fig. 1 where a typical ''isotherm'' is drawn (black curve). The Maxwell construction is a way of correcting this deficiency. The decreasing right hand part of the curve in Fig. 1 describes a diluted gas, while its left part describes a liquid. The intermediate (rising) part of the curve in Fig. 1 would be correct, if these two parts were to be joined smoothly—meaning in particular that the system would remain also in this region spatially uniform with a well defined density. But this is not what happens. If the volume of a vessel containing a fixed amount of liquid is expanded at constant temperature, there comes a point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Demon
Maxwell's demon is a thought experiment that would hypothetically violate the second law of thermodynamics. It was proposed by the physicist James Clerk Maxwell in 1867. In his first letter Maxwell called the demon a "finite being", while the ''Daemon'' name was first used by Lord Kelvin. In the thought experiment, a demon controls a small massless door between two chambers of gas. As individual gas molecules (or atoms) approach the door, the demon quickly opens and closes the door to allow only fast-moving molecules to pass through in one direction, and only slow-moving molecules to pass through in the other. Because the kinetic temperature of a gas depends on the velocities of its constituent molecules, the demon's actions cause one chamber to warm up and the other to cool down. This would decrease the total entropy of the two gases, without applying any work, thereby violating the second law of thermodynamics. The concept of Maxwell's demon has provoked substantial debate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |