|
Z Combinator
In combinatory logic for computer science, a fixed-point combinator (or fixpoint combinator) is a higher-order function (i.e., a function which takes a function as argument) that returns some '' fixed point'' (a value that is mapped to itself) of its argument function, if one exists. Formally, if \mathrm is a fixed-point combinator and the function f has one or more fixed points, then \mathrm\ f is one of these fixed points, i.e., : \mathrm\ f\ = f\ (\mathrm\ f) . Fixed-point combinators can be defined in the lambda calculus and in functional programming languages, and provide a means to allow for recursive definitions. ''Y'' combinator in lambda calculus In the classical untyped lambda calculus, every function has a fixed point. A particular implementation of \mathrm is Haskell Curry's paradoxical combinator ''Y'', given byThroughout this article, the syntax rules given in Lambda calculus#Notation are used, to save parentheses.According to Barendregt p.132, the name originat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatory Logic
Combinatory logic is a notation to eliminate the need for quantified variables in mathematical logic. It was introduced by Moses Schönfinkel and Haskell Curry, and has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming languages. It is based on combinators, which were introduced by Schönfinkel in 1920 with the idea of providing an analogous way to build up functions—and to remove any mention of variables—particularly in predicate logic. A combinator is a higher-order function that uses only function application and earlier defined combinators to define a result from its arguments. In mathematics Combinatory logic was originally intended as a 'pre-logic' that would clarify the role of quantified variables in logic, essentially by eliminating them. Another way of eliminating quantified variables is Quine's predicate functor logic. While the expressive power of combinatory log ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lazy Evaluation
In programming language theory, lazy evaluation, or call-by-need, is an evaluation strategy which delays the evaluation of an Expression (computer science), expression until its value is needed (non-strict evaluation) and which avoids repeated evaluations (by the use of Sharing (computer science), sharing). The benefits of lazy evaluation include: * The ability to define control flow (structures) as abstractions instead of Language primitive, primitives. * The ability to define actual infinity, potentially infinite data structures. This allows for more straightforward implementation of some algorithms. * The ability to define partly-defined data structures where some elements are errors. This allows for rapid prototyping. Lazy evaluation is often combined with memoization, as described in Jon Bentley (computer scientist), Jon Bentley's ''Writing Efficient Programs''. After a function's value is computed for that Parameter (computer programming), parameter or set of parameters, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensionality
In logic, extensionality, or extensional equality, refers to principles that judge objects to be equality (mathematics), equal if they have the same external properties. It stands in contrast to the concept of intensionality, which is concerned with whether the internal definitions of objects are the same. In mathematics The extensional definition of function equality, discussed above, is commonly used in mathematics. A similar extensional definition is usually employed for relation (mathematics), relations: two relations are said to be equal if they have the same Extension (predicate logic), extensions. In set theory, the axiom of extensionality states that two set (mathematics), sets are equal if and only if they contain the same elements. In mathematics formalized in set theory, it is common to identify relations—and, most importantly, function (mathematics), functions—with their extension as stated above, so that it is impossible for two relations or functions with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive integers Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the ''whole numbers'' refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are ''six'' coins on the table", in which case they are called ''cardinal numbers''. They are also used to put things in order, like "this is the ''third'' largest city in the country", which are called ''ordinal numbers''. Natural numbers are also used as labels, like Number (sports), jersey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain Of A Function
In mathematics, the domain of a function is the Set (mathematics), set of inputs accepted by the Function (mathematics), function. It is sometimes denoted by \operatorname(f) or \operatornamef, where is the function. In layman's terms, the domain of a function can generally be thought of as "what x can be". More precisely, given a function f\colon X\to Y, the domain of is . In modern mathematical language, the domain is part of the definition of a function rather than a property of it. In the special case that and are both sets of real numbers, the function can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the -axis of the graph, as the projection of the graph of the function onto the -axis. For a function f\colon X\to Y, the set is called the ''codomain'': the set to which all outputs must belong. The set of specific outputs the function assigns to elements of is called its ''Range of a function, range'' or ''Image (mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Church Encoding
In mathematics, Church encoding is a means of representing data and operators in the lambda calculus. The Church numerals are a representation of the natural numbers using lambda notation. The method is named for Alonzo Church, who first encoded data in the lambda calculus this way. Terms that are usually considered primitive in other notations (such as integers, Booleans, pairs, lists, and tagged unions) are mapped to higher-order functions under Church encoding. The Church–Turing thesis asserts that any computable operator (and its operands) can be represented under Church encoding. In the untyped lambda calculus the only primitive data type is the function. Use A straightforward implementation of Church encoding slows some access operations from O(1) to O(n), where n is the size of the data structure, making Church encoding impractical. Research has shown that this can be addressed by targeted optimizations, but most functional programming languages instead expand their i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imperative Programming
In computer science, imperative programming is a programming paradigm of software that uses Statement (computer science), statements that change a program's state (computer science), state. In much the same way that the imperative mood in natural languages expresses commands, an imperative program consists of command (computing), commands for the computer to perform. Imperative programming focuses on describing ''how'' a program operates step by step (with general order of the steps being determined in source code by the placement of statements one below the other), rather than on high-level descriptions of its expected results. The term is often used in contrast to declarative programming, which focuses on ''what'' the program should accomplish without specifying all the details of ''how'' the program should achieve the result. Procedural programming Procedural programming is a type of imperative programming in which the program is built from one or more procedures (also termed s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Programming
In computer science, functional programming is a programming paradigm where programs are constructed by Function application, applying and Function composition (computer science), composing Function (computer science), functions. It is a declarative programming paradigm in which function definitions are Tree (data structure), trees of Expression (computer science), expressions that map Value (computer science), values to other values, rather than a sequence of Imperative programming, imperative Statement (computer science), statements which update the State (computer science), running state of the program. In functional programming, functions are treated as first-class citizens, meaning that they can be bound to names (including local Identifier (computer languages), identifiers), passed as Parameter (computer programming), arguments, and Return value, returned from other functions, just as any other data type can. This allows programs to be written in a Declarative programming, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Typed Lambda Calculus
A typed lambda calculus is a typed formalism that uses the lambda symbol (\lambda) to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered (see kinds below). From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus, but from another point of view, they can also be considered the more fundamental theory and ''untyped lambda calculus'' a special case with only one type. Typed lambda calculi are foundational programming languages and are the base of typed functional programming languages such as ML and Haskell and, more indirectly, typed imperative programming languages. Typed lambda calculi play an important role in the design of type systems for programming languages; here, typability usually captures desirable properties of the program (e.g., the program will not cause a memory acce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
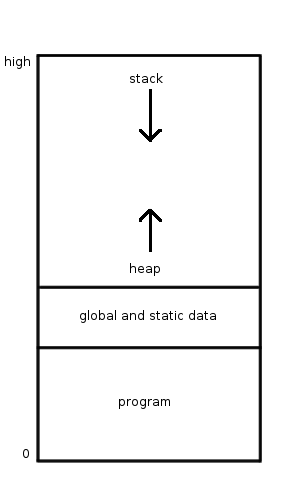
Stack Overflow
In software, a stack overflow occurs if the call stack pointer exceeds the stack bound. The call stack may consist of a limited amount of address space, often determined at the start of the program. The size of the call stack depends on many factors, including the programming language, machine architecture, multi-threading, and amount of available memory. When a program attempts to use more space than is available on the call stack (that is, when it attempts to access memory beyond the call stack's bounds, which is essentially a buffer overflow), the stack is said to ''overflow'', typically resulting in a program crash. Causes Infinite recursion The most-common cause of stack overflow is excessively deep or infinite recursion, in which a function calls itself so many times that the space needed to store the variables and information associated with each call is more than can fit on the stack. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Loop
In computer programming, an infinite loop (or endless loop) is a sequence of instructions that, as written, will continue endlessly, unless an external intervention occurs, such as turning off power via a switch or pulling a plug. It may be intentional. There is no general algorithm to determine whether a computer program contains an infinite loop or not; this is the halting problem. Overview This differs from "a type of computer program that runs the same instructions continuously until it is either stopped or interrupted". Consider the following pseudocode: how_many = 0 while is_there_more_data() do how_many = how_many + 1 end display "the number of items counted = " how_many ''The same instructions'' were run ''continuously until it was stopped or interrupted'' . . . by the ''FALSE'' returned at some point by the function ''is_there_more_data''. By contrast, the following loop will not end by itself: birds = 1 fish = 2 while birds + fish > 1 do birds = 3 - bird ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |