|
Vanishing Puzzle
A vanishing puzzle is a mechanical optical illusion comprising multiple pieces which can be rearranged to show different versions of a picture depicting several objects, the number of which depending on the arrangement of the pieces. History Wemple & Company marketed an advertising card named ''The Magic Egg Puzzle, (How Many Eggs?)'' in New York in 1880. Cutting the rectangular card into four oblongs allowed the pieces to be rearranged to show either 8, 9 or 10 eggs. Many other similar puzzles have been published since. Chess player and recreational mathematician Sam Loyd patented rotary vanishing puzzles in 1896 and published versions named ''Get Off the Earth'', ''Teddy and the Lion'' and ''The Disappearing Bicyclist'' (pictured). Each had a circular card connected to a cardboard backdrop with a pin, letting it freely rotate. In ''The Disappearing Bicyclist'', when the disc is rotated such that the arrow points to A, 13 boys can be counted, but when it points to B, there ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Disappearing Bicyclist Vanishing Puzzle
''The'' () is a grammatical article in English, denoting persons or things already mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with pronouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of pronoun ''thee'') when followed by a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
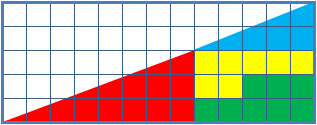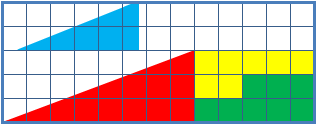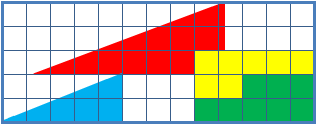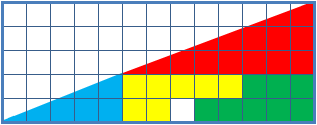
Missing Square Puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recreational Mathematics
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research and application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults, inspiring their further study of the subject. The Mathematical Association of America (MAA) includes recreational mathematics as one of its seventeen Special Interest Groups, commenting: Mathematical competitions (such as those sponsored by mathematical associations) are also categorized under recreational mathematics. Topics Some of the more well-known topics in recreational mathematics are Rubik's Cubes, magic squares, fractals, logic puzzles and mathematical chess problems, but this area of mathematics incl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Paradoxes
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusions
Within visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Dollar Riddle
The missing dollar riddle is a famous riddle that involves an informal fallacy. It dates to at least the 1930s, although similar puzzles are much older. Statement Although the wording and specifics can vary, the puzzle runs along these lines: Three guests check into a hotel room. The manager says the bill is $30, so each guest pays $10. Later the manager realizes the bill should only have been $25. To rectify this, he gives the bellhop $5 as five one-dollar bills to return to the guests. On the way to the guests' room to refund the money, the bellhop realizes that he cannot equally divide the five one-dollar bills among the three guests. As the guests are not aware of the total of the revised bill, the bellhop decides to just give each guest $1 back and keep $2 as a tip for himself, and proceeds to do so. As each guest got $1 back, each guest only paid $9, bringing the total paid to $27. The bellhop kept $2, which when added to the $27, comes to $29. So if the guests originall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooper's Paradox
Hooper's paradox is a falsidical paradox based on an optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units. Explanation Upon close inspection one can notice that the triangles of the dissected shape are not identical to the triangles in the rectangle. The length of the shorter side at the right angle measures 2 units in the original shape but only 1.8 units in the rectangle. This means, the real triangles of the original shape overlap in the rectangle. The overlapping area is a parallelogram, the diagonals and sides of which can be computed via the Pythagorean theorem. : d_1=\sqrt=\sqrt : d_2=\sqrt=\sqrt : s_1=\sqrt=\sqrt : s_2=\sqrt=\sqrt The area of this parallelogram can determined using Heron's formula for triangles. This yields : s=\frac=\frac for the halved circumference of the triangle (half of the parallelogram) and with that for the area of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstellung Effect
Einstellung () is the development of a mechanized state of mind. Often called a problem solving set, Einstellung refers to a person's predisposition to solve a given problem in a specific manner even though better or more appropriate methods of solving the problem exist. The Einstellung effect is the negative effect of previous experience when solving new problems. The Einstellung effect has been tested experimentally in many different contexts. The most famous example (which led to the coining of the term by Abraham S. Luchins and Edith Hirsch, Edith Hirsch Luchins) is the Luchins water jar experiment, in which subjects were asked to solve a series of water pouring puzzle, water jar problems. After solving many problems which had the same solution, subjects applied the same solution to later problems even though a simpler solution existed (Luchins, 1942).. Other experiments on the Einstellung effect can be found in ''The Effect of Einstellung on Compositional Processes'' and ''Ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Puzzle
A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces in which the solution is to manipulate the whole object or parts of it. While puzzles of this type have been in use by humanity as early as the 3rd century BC, one of the most well-known mechanical puzzles of modern day is the Rubik's Cube, invented by the Hungarian architect Ernő Rubik in 1974. The puzzles are typically designed for a single player, where the goal is for the player to see through the principle of the object, rather than accidentally coming up with the right solution through trial and error. With this in mind, they are often used as an intelligence test or in problem solving training. History The oldest known mechanical puzzle comes from Greece and appeared in the 3rd century BC. The game consists of a square divided into 14 parts, and the aim was to create different shapes from these pieces. This is not easy to do. (see Ostomachion loculus Archimedius) In Iran "puzzle-lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-Collinearity, collinear, determine a unique triangle and simultaneously, a unique Plane (mathematics), plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> The Disappearing Bicyclist Vanishing Puzzle")
