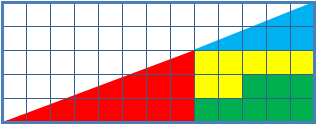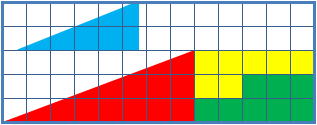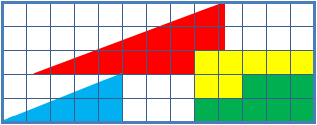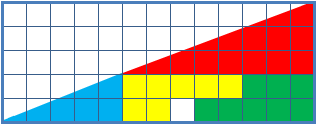
|
Missing Square Puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Square Animation
Missing or The Missing may refer to: Film *Missing (1918 film), ''Missing'' (1918 film), an American silent drama directed by James Young *Missing (1982 film), ''Missing'' (1982 film), an American historical drama directed by Costa-Gavras *Missing (2007 film), ''Missing'' (2007 film) (''Vermist''), a Belgian film that was a List of 2007 box office number-one films in Belgium, 2007 box office number-one film in Belgium *Missing (2008 film), ''Missing'' (2008 film), a Hong Kong horror film directed by Tsui Hark *Missing (2009 film), ''Missing'' (2009 film), a List of South Korean films of 2009, South Korean film directed by Kim Sung-hong *Missing (2009 short film), ''Missing'' (2009 short film), a film starring Susan Glover *Missing (2010 film), ''Missing'' (2010 film), a List of Jordanian films, Jordanian film directed by Tariq Rimawi *Missing (2016 film), ''Missing'' (2016 film), a South Korean film directed by Lee Eon-hee *Missing (2018 film), ''Missing'' (2018 film), an Indian f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Paradoxes
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. In the Canadian curriculum, there are six basic strands in Elementary Mathematics: Number, Algebra, Data, Spatial Sense, Financial Literacy, and Social emotional learning skills and math processes. These six strands are the focus of Mathematics education from grade 1 through grade 8. In secondary school, the main topics in elementary mathematics from grade nine until grade ten are: Number Sense and algebra, Linear Relations, Measurement and Geometry. Once students enter grade eleven and twelve students begin university and college preparation classes, which include: Functions, Calculus & Vectors, Advanced Functions, and Data Management. Strands of elementary mathematics Number Sense and Numeration Number Sense is an understanding of numbers and operations. In the 'Number Sense and Numeration' strand students develop an understanding of numbers by being taught ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusions
Within visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chocolate Bar
A chocolate bar (Commonwealth English) or candy bar (some dialects of American English) is a confection containing chocolate, which may also contain layerings or mixtures that include nuts, fruit, caramel, nougat, and wafers. A flat, easily breakable, chocolate bar is also called a tablet. A wide variety of chocolate bar brands are sold. A popular example is a Snickers bar, which consists of nougat mixed with caramel and peanuts, covered in milk chocolate. The first solid chocolate bar put into production was made by J. S. Fry & Sons of Bristol, England, in 1847. Cadbury began producing one in 1849. Released in 1866, a filled chocolate bar, Fry's Chocolate Cream, was the first mass-produced chocolate bar. In 1912, the Goo Goo Cluster was the first mass-produced combination bar; it included marshmallow, nougat, caramel, and roasted peanuts. In some varieties of English and food labeling standards, the term ''chocolate bar'' is reserved for bars of solid chocolate, with ''candy b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet-born Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Mathematics, senior instructor at Hebrew University and software consultant at Ben Gurion University. He wrote extensively about arithmetic, probability, algebra, geometry, trigonometry and mathematical games. He was known for his contribution to heuristics and mathematics education, creating and maintaining the mathematically themed educational website ''Cut-the-Knot'' for the Mathematical Association of America (MAA) Online. He was a pioneer in mathematical education on the internet, having started ''Cut-the-Knot'' in October 1996.Interview with Alexander ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Dollar Riddle
The missing dollar riddle is a famous riddle that involves an informal fallacy. It dates to at least the 1930s, although similar puzzles are much older. Statement Although the wording and specifics can vary, the puzzle runs along these lines: Three guests check into a hotel room. The manager says the bill is $30, so each guest pays $10. Later the manager realizes the bill should only have been $25. To rectify this, he gives the bellhop $5 as five one-dollar bills to return to the guests. On the way to the guests' room to refund the money, the bellhop realizes that he cannot equally divide the five one-dollar bills among the three guests. As the guests are not aware of the total of the revised bill, the bellhop decides to just give each guest $1 back and keep $2 as a tip for himself, and proceeds to do so. As each guest got $1 back, each guest only paid $9, bringing the total paid to $27. The bellhop kept $2, which when added to the $27, comes to $29. So if the guests originall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooper's Paradox
Hooper's paradox is a falsidical paradox based on an optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units. Explanation Upon close inspection one can notice that the triangles of the dissected shape are not identical to the triangles in the rectangle. The length of the shorter side at the right angle measures 2 units in the original shape but only 1.8 units in the rectangle. This means, the real triangles of the original shape overlap in the rectangle. The overlapping area is a parallelogram, the diagonals and sides of which can be computed via the Pythagorean theorem. : d_1=\sqrt=\sqrt : d_2=\sqrt=\sqrt : s_1=\sqrt=\sqrt : s_2=\sqrt=\sqrt The area of this parallelogram can determined using Heron's formula for triangles. This yields : s=\frac=\frac for the halved circumference of the triangle (half of the parallelogram) and with that for the area of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstellung Effect
Einstellung () is the development of a mechanized state of mind. Often called a problem solving set, Einstellung refers to a person's predisposition to solve a given problem in a specific manner even though better or more appropriate methods of solving the problem exist. The Einstellung effect is the negative effect of previous experience when solving new problems. The Einstellung effect has been tested experimentally in many different contexts. The most famous example (which led to the coining of the term by Abraham S. Luchins and Edith Hirsch, Edith Hirsch Luchins) is the Luchins water jar experiment, in which subjects were asked to solve a series of water pouring puzzle, water jar problems. After solving many problems which had the same solution, subjects applied the same solution to later problems even though a simpler solution existed (Luchins, 1942).. Other experiments on the Einstellung effect can be found in ''The Effect of Einstellung on Compositional Processes'' and ''Ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant (trigonometry)
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
