|
Underdetermined System
In mathematics, a system of linear equations or a system of polynomial equations is considered underdetermined if there are fewer equations than unknowns (in contrast to an overdetermined system, where there are more equations than unknowns). The terminology can be explained using the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case (between overdetermined and underdetermined) occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint removing a degree of freedom. The underdetermined case, by contrast, occurs when the system has been underconstrained—that is, when the unknowns outnumber the equations. Solutions of underdetermined systems An underdetermined linear system has either no sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraically Closed Field
In mathematics, a field is algebraically closed if every non-constant polynomial in (the univariate polynomial ring with coefficients in ) has a root in . Examples As an example, the field of real numbers is not algebraically closed, because the polynomial equation ''x''2 + 1 = 0 has no solution in real numbers, even though all its coefficients (1 and 0) are real. The same argument proves that no subfield of the real field is algebraically closed; in particular, the field of rational numbers is not algebraically closed. Also, no finite field ''F'' is algebraically closed, because if ''a''1, ''a''2, ..., ''an'' are the elements of ''F'', then the polynomial (''x'' − ''a''1)(''x'' − ''a''2) ⋯ (''x'' − ''a''''n'') + 1 has no zero in ''F''. By contrast, the fundamental theorem of algebra states that the field of complex numbers is algebraically closed. Another example of an algebraicall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdetermined System
In mathematics, a system of equations is considered overdetermined if there are more equations than unknowns. An overdetermined system is almost always inconsistent (it has no solution) when constructed with random coefficients. However, an overdetermined system will have solutions in some cases, for example if some equation occurs several times in the system, or if some equations are linear combinations of the others. The terminology can be described in terms of the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint. The ''overdetermined'' case occurs when the system has been overconstrained — that is, when the equations outnumb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series of sampling measurements. In general, this task is impossible because there is no way to reconstruct a signal during the times that the signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
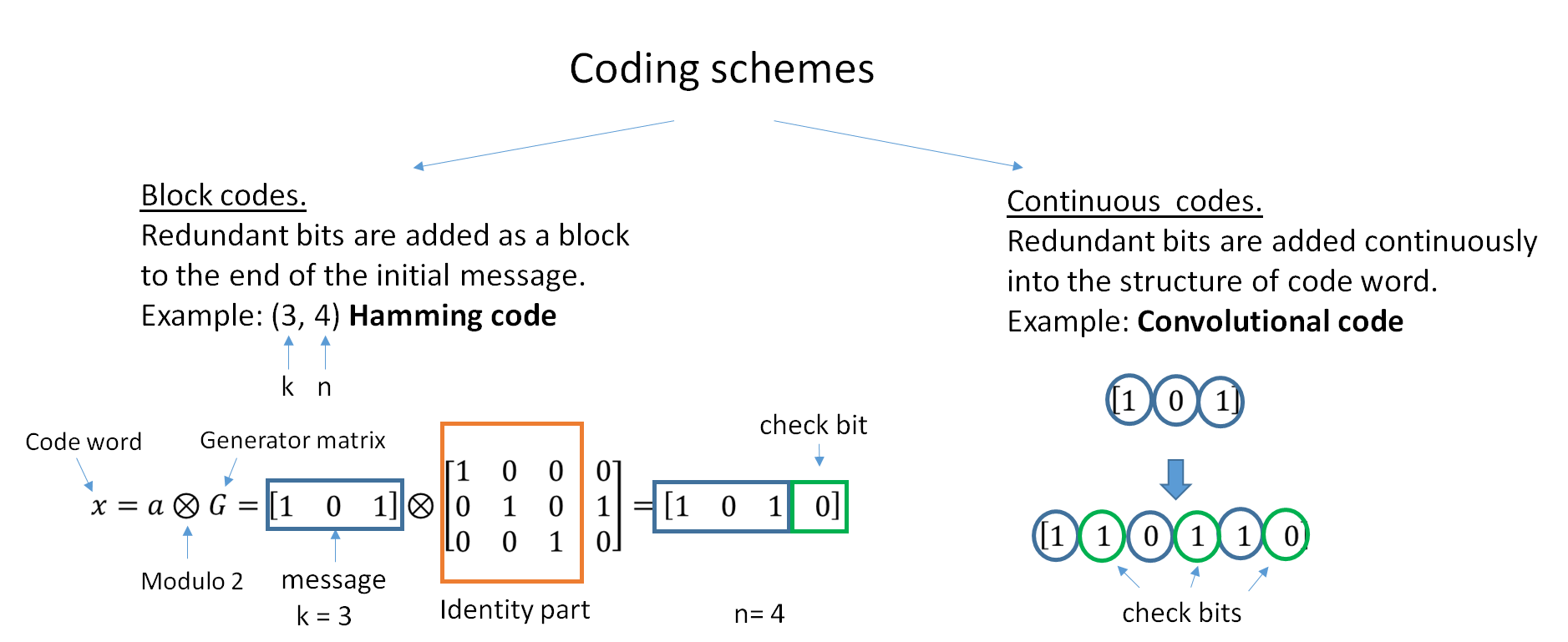
Error Correcting Codes
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error control (or ''channel coding'') # Cryptographic coding # Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, ZIP data compression makes data files smaller, for purposes such as to reduce Internet traffic. Data compression a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diophantine Equations
In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, such that the only solutions of interest are the integer ones. A linear Diophantine equation equates to a constant the sum of two or more monomials, each of degree one. An exponential Diophantine equation is one in which unknowns can appear in exponents. Diophantine problems have fewer equations than unknowns and involve finding integers that solve simultaneously all equations. As such systems of equations define algebraic curves, algebraic surfaces, or, more generally, algebraic sets, their study is a part of algebraic geometry that is called ''Diophantine geometry''. The word ''Diophantine'' refers to the Hellenistic mathematician of the 3rd century, Diophantus of Alexandria, who made a study of such equations and was one of the first mathematicians to introduce symbolism into algebra. The mathematical study of Diophantine problems that Di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Programming
An integer programming problem is a mathematical optimization or Constraint satisfaction problem, feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are Linear function (calculus), linear. Integer programming is NP-complete. In particular, the special case of 0-1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp's 21 NP-complete problems. If some decision variables are not discrete, the problem is known as a mixed-integer programming problem. Canonical and standard form for ILPs In integer linear programming, the ''canonical form'' is distinct from the ''standard form''. An integer linear program in canonical form is expressed thus (note that it is the \mathbf vector which is to be decided): : \begin & \text && \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Objective Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |