|
Unit Quaternion
In mathematics, a versor is a quaternion of norm one (a ''unit quaternion''). The word is derived from Latin ''versare'' = "to turn" with the suffix ''-or'' forming a noun from the verb (i.e. ''versor'' = "the turner"). It was introduced by William Rowan Hamilton in the context of his quaternion theory. Each versor has the form :q = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is a unit-length vector quaternion (or that the first component of r is zero, and the last three components of r are a unit vector in 3 dimensions). The corresponding 3-dimensional rotation has the angle 2''a'' about the axis r in axis–angle representation. In case (a right angle), then q = \mathbf, and the resulting unit vector is termed a ''right versor''. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U''q''. He was then able to display the general quaternion in polar coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
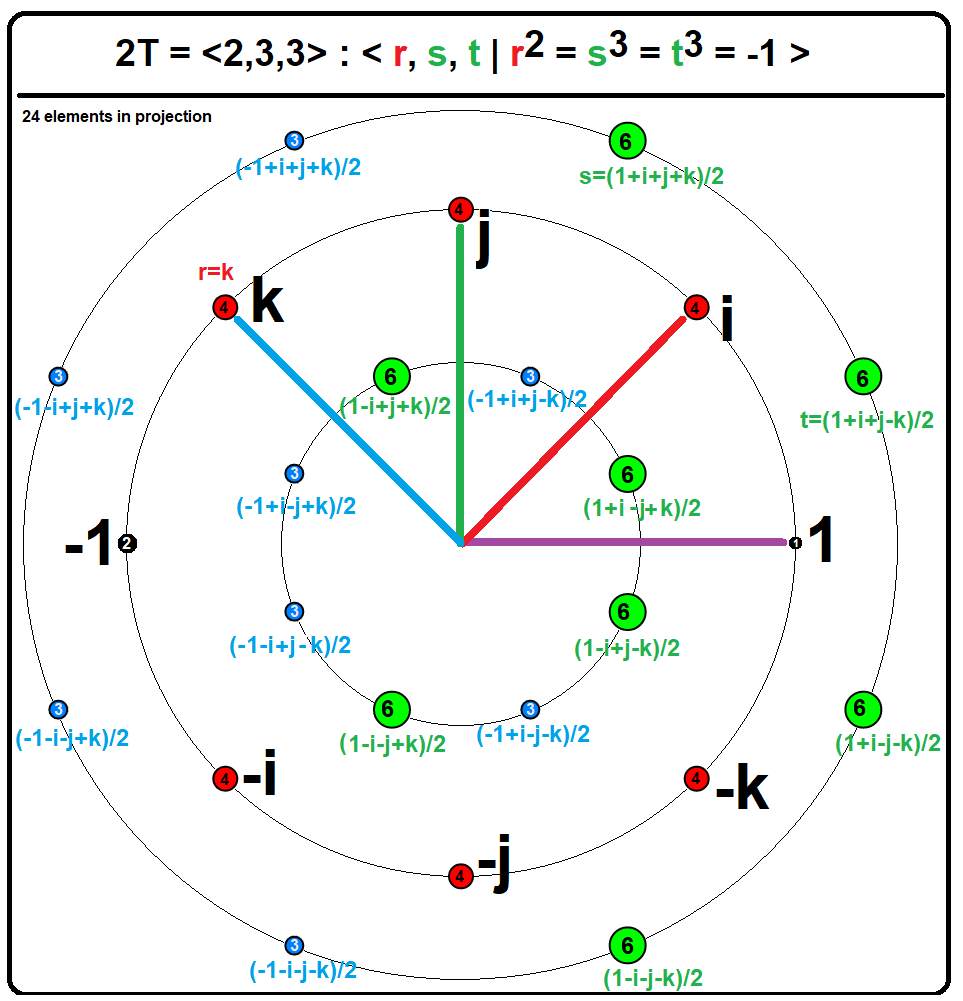
Hurwitz Quaternion
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. Struct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection Point
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their intersection is the point at which they meet. More generally, in set theory, the intersection of sets is defined to be the set of elements which belong to all of them. Unlike the Euclidean definition, this does not presume that the objects under consideration lie in a common space. Intersection is one of the basic concepts of geometry. An intersection can have various geometric shapes, but a point is the most common in a plane geometry. Incidence geometry defines an intersection (usually, of flats) as an object of lower dimension that is incident to each of original objects. In this approach an intersection can be sometimes undefined, such as for parallel lines. In both cases the concept of intersection relies on logical conjunction. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. Definitions A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes. Two elements of the given set are equivalent to each other if and only if they belong to the same equivalence class. Notation Various notations are used in the literature to denote that two elements a and b of a set are equivalent with respect to an equivalence relation R; the most common are "a \sim b" and "", which are used when R is implicit, and variations of "a \sim_R b", "", or "" to specify R explicitly. Non-equivalence may be written "" or "a \not\equiv b". Definition A binary relation \,\sim\, on a set X is said to be an equivalence relation, if and only if it is reflexive, symmetric and transitive. That is, for all a, b, and c in X: * a \sim a ( ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Sphere
In mathematics, a unit sphere is simply a sphere of radius one around a given center. More generally, it is the set of points of distance 1 from a fixed central point, where different norms can be used as general notions of "distance". A unit ball is the closed set of points of distance less than or equal to 1 from a fixed central point. Usually the center is at the origin of the space, so one speaks of "the unit ball" or "the unit sphere". Special cases are the unit circle and the unit disk. The importance of the unit sphere is that any sphere can be transformed to a unit sphere by a combination of translation and scaling. In this way the properties of spheres in general can be reduced to the study of the unit sphere. Unit spheres and balls in Euclidean space In Euclidean space of ''n'' dimensions, the -dimensional unit sphere is the set of all points (x_1, \ldots, x_n) which satisfy the equation : x_1^2 + x_2^2 + \cdots + x_n ^2 = 1. The ''n''-dimensional open unit ball ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest circle that c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Geometry
300px, A sphere with a spherical triangle on it. Spherical geometry is the geometry of the two-dimensional surface of a sphere. In this context the word "sphere" refers only to the 2-dimensional surface and other terms like "ball" or "solid sphere" are used for the surface together with its 3-dimensional interior. Long studied for its practical applications to navigation and astronomy, spherical geometry bears many similarities and relationships to, and important differences from, Euclidean plane geometry. The sphere has for the most part been studied as a part of 3-dimensional Euclidean geometry (often called solid geometry), the surface thought of as placed inside an ambient 3-d space. It can also be analyzed by "intrinsic" methods that only involve the surface itself, and do not refer to, or even assume the existence of, any surrounding space outside or inside the sphere. Because a sphere and a plane differ geometrically, (intrinsic) spherical geometry has some featu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using a line above the symbols for the two endpoints (such as \overline). Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. When the end points both lie on a curve (such as a circle), a line segment is called a chord (geometry), chord (of that curve). In real or complex vector spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc (geometry)
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is €¦the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which €¦will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |