|
Two-sided Error
In computing, a Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. Two examples of such algorithms are Karger–Stein algorithm and Monte Carlo algorithm for minimum Feedback arc set. The name refers to the grand casino in the Principality of Monaco at Monte Carlo, which is well-known around the world as an icon of gambling. The term "Monte Carlo" was first introduced in 1947 by Nicholas Metropolis. Las Vegas algorithms are a dual of Monte Carlo algorithms that never return an incorrect answer. However, they may make random choices as part of their work. As a result, the time taken might vary between runs, even with the same input. If there is a procedure for verifying whether the answer given by a Monte Carlo algorithm is correct, and the probability of a correct answer is bounded above zero, then with probability, one running the algorithm repeatedly while testing the answers will eventually give a corre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computing
Computing is any goal-oriented activity requiring, benefiting from, or creating computing machinery. It includes the study and experimentation of algorithmic processes, and development of both hardware and software. Computing has scientific, engineering, mathematical, technological and social aspects. Major computing disciplines include computer engineering, computer science, cybersecurity, data science, information systems, information technology and software engineering. The term "computing" is also synonymous with counting and calculating. In earlier times, it was used in reference to the action performed by mechanical computing machines, and before that, to human computers. History The history of computing is longer than the history of computing hardware and includes the history of methods intended for pen and paper (or for chalk and slate) with or without the aid of tables. Computing is intimately tied to the representation of numbers, though mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complexity Class
In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and memory. In general, a complexity class is defined in terms of a type of computational problem, a model of computation, and a bounded resource like time or memory. In particular, most complexity classes consist of decision problems that are solvable with a Turing machine, and are differentiated by their time or space (memory) requirements. For instance, the class P is the set of decision problems solvable by a deterministic Turing machine in polynomial time. There are, however, many complexity classes defined in terms of other types of problems (e.g. counting problems and function problems) and using other models of computation (e.g. probabilistic Turing machines, interactive proof systems, Boolean circuits, and quantum computers). The study of the relationships between complexity class ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New York City
New York, often called New York City or NYC, is the most populous city in the United States. With a 2020 population of 8,804,190 distributed over , New York City is also the most densely populated major city in the United States, and is more than twice as populous as second-place Los Angeles. New York City lies at the southern tip of New York State, and constitutes the geographical and demographic center of both the Northeast megalopolis and the New York metropolitan area, the largest metropolitan area in the world by urban landmass. With over 20.1 million people in its metropolitan statistical area and 23.5 million in its combined statistical area as of 2020, New York is one of the world's most populous megacities, and over 58 million people live within of the city. New York City is a global cultural, financial, entertainment, and media center with a significant influence on commerce, health care and life sciences, research, technology, educa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atlantic City Algorithm
Atlantic City algorithm is a probabilistic polynomial time algorithm that answers correctly at least 75% of the time (or, in some versions, some other value greater than 50%). The term "Atlantic City" was first introduced in 1982 by J. Finn in an unpublished manuscript entitled ''Comparison of probabilistic tests for primality''. Two other common classes of probabilistic algorithms are Monte Carlo algorithms and Las Vegas algorithms. Monte Carlo algorithms are always fast, but only probably correct. On the other hand, Las Vegas algorithms are always correct, but only probably fast. The Atlantic City algorithms, which are bounded probabilistic polynomial time algorithms are probably correct and probably fast. See also * Monte Carlo Algorithm * Las Vegas Algorithm In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. However, the runtime of a Las Vegas algor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Statistics
Computational statistics, or statistical computing, is the bond between statistics and computer science. It means statistical methods that are enabled by using computational methods. It is the area of computational science (or scientific computing) specific to the mathematical science of statistics. This area is also developing rapidly, leading to calls that a broader concept of computing should be taught as part of general statistical education. As in traditional statistics the goal is to transform raw data into knowledge, Wegman, Edward J. �Computational Statistics: A New Agenda for Statistical Theory and Practice.�� Journal of the Washington Academy of Sciences', vol. 78, no. 4, 1988, pp. 310–322. ''JSTOR'' but the focus lies on computer intensive statistical methods, such as cases with very large sample size and non-homogeneous data sets. The terms 'computational statistics' and 'statistical computing' are often used interchangeably, although Carlo Lauro (a former p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
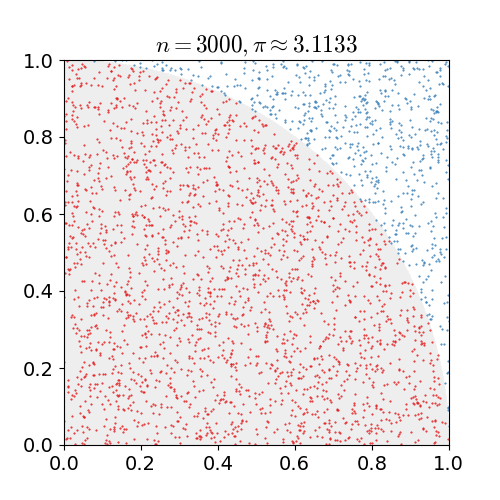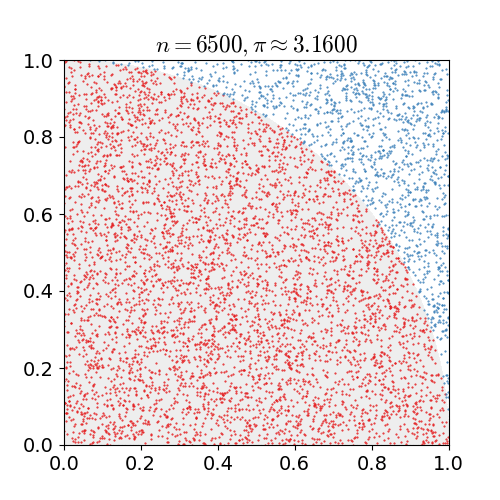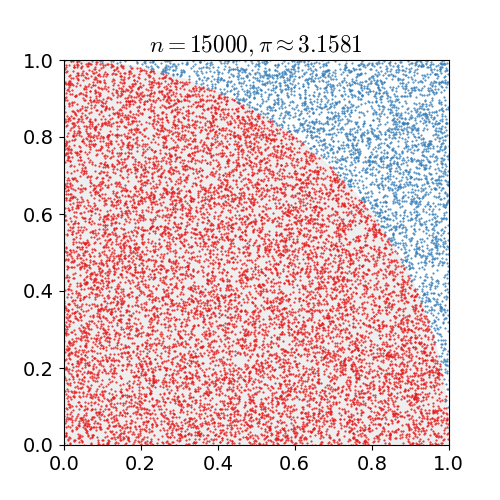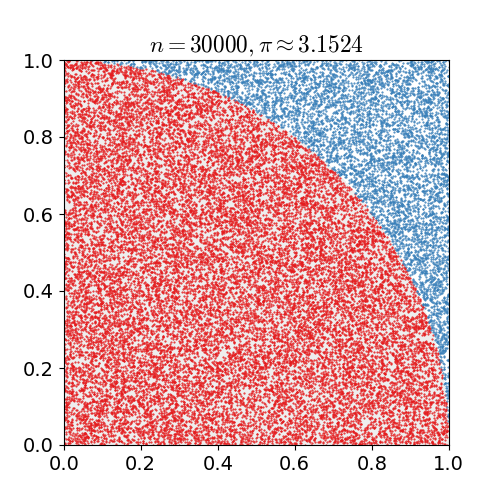
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Group Theory
In mathematics, computational group theory is the study of group (mathematics), groups by means of computers. It is concerned with designing and analysing algorithms and data structures to compute information about groups. The subject has attracted interest because for many interesting groups (including most of the sporadic groups) it is impractical to perform calculations by hand. Important algorithms in computational group theory include: * the Schreier–Sims algorithm for finding the order (group theory), order of a permutation group * the Todd–Coxeter algorithm and Knuth–Bendix algorithm for coset enumeration * the product-replacement algorithm for finding random elements of a group Two important computer algebra systems (CAS) used for group theory are GAP computer algebra system, GAP and Magma computer algebra system, Magma. Historically, other systems such as CAS (for character theory) and Cayley computer algebra system, Cayley (a predecessor of Magma) were important. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schreier–Sims Algorithm
The Schreier–Sims algorithm is an algorithm in computational group theory, named after the mathematicians Otto Schreier and Charles Sims. This algorithm can find the order of a finite permutation group, test membership (is a given permutation contained in a group?), and many other tasks in polynomial time. It was introduced by Sims in 1970, based on Schreier's subgroup lemma. The timing was subsequently improved by Donald Knuth in 1991. Later, an even faster randomized version of the algorithm was developed. Background and timing The algorithm is an efficient method of computing a base and strong generating set (BSGS) of a permutation group. In particular, an SGS determines the order of a group and makes it easy to test membership in the group. Since the SGS is critical for many algorithms in computational group theory, computer algebra systems typically rely on the Schreier–Sims algorithm for efficient calculations in groups. The running time of Schreier–Sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miller–Rabin Primality Test
The Miller–Rabin primality test or Rabin–Miller primality test is a probabilistic primality test: an algorithm which determines whether a given number is likely to be prime, similar to the Fermat primality test and the Solovay–Strassen primality test. It is of historical significance in the search for a polynomial-time deterministic primality test. Its probabilistic variant remains widely used in practice, as one of the simplest and fastest tests known. Gary L. Miller discovered the test in 1976; Miller's version of the test is deterministic, but its correctness relies on the unproven extended Riemann hypothesis. Michael O. Rabin modified it to obtain an unconditional probabilistic algorithm in 1980. Mathematical concepts Similarly to the Fermat and Solovay–Strassen tests, the Miller–Rabin primality test checks whether a specific property, which is known to hold for prime values, holds for the number under testing. Strong probable primes The property is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Baillie–PSW Primality Test
The Baillie–PSW primality test is a probabilistic primality testing algorithm that determines whether a number is composite or is a probable prime. It is named after Robert Baillie, Carl Pomerance, John Selfridge, and Samuel Wagstaff. The Baillie–PSW test is a combination of a strong Fermat probable prime test to base 2 and a strong Lucas probable prime test. The Fermat and Lucas test each have their own list of pseudoprimes, that is, composite numbers that pass the test. For example, the first ten strong pseudoprimes to base 2 are : 2047, 3277, 4033, 4681, 8321, 15841, 29341, 42799, 49141, and 52633 . The first ten strong Lucas pseudoprimes (with Lucas parameters (''P'', ''Q'') defined by Selfridge's Method A) are : 5459, 5777, 10877, 16109, 18971, 22499, 24569, 25199, 40309, and 58519 . There is no known overlap between these lists of strong Fermat pseudoprimes and strong Lucas pseudoprimes, and there is even evidence that the numbers in these lists tend to be different ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time. The complexity class was defined by Gill in 1977. If a decision problem is in PP, then there is an algorithm for it that is allowed to flip coins and make random decisions. It is guaranteed to run in polynomial time. If the answer is YES, the algorithm will answer YES with probability more than 1/2. If the answer is NO, the algorithm will answer YES with probability less than 1/2. In more practical terms, it is the class of problems that can be solved to any fixed degree of accuracy by running a randomized, polynomial-time algorithm a sufficient (but bounded) number of times. Turing machines that are polynomially-bound and probabilistic are characterized as PPT, which stands for probabilistic polynomial-time machines. This characterizatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ZPP (complexity)
In complexity theory, ZPP (zero-error probabilistic polynomial time) is the complexity class of problems for which a probabilistic Turing machine exists with these properties: * It always returns the correct YES or NO answer. * The running time is polynomial in expectation for every input. In other words, if the algorithm is allowed to flip a truly-random coin while it is running, it will always return the correct answer and, for a problem of size ''n'', there is some polynomial ''p''(''n'') such that the average running time will be less than ''p''(''n''), even though it might occasionally be much longer. Such an algorithm is called a Las Vegas algorithm. Alternatively, ZPP can be defined as the class of problems for which a probabilistic Turing machine exists with these properties: * It always runs in polynomial time. * It returns an answer YES, NO or DO NOT KNOW. * The answer is always either DO NOT KNOW or the correct answer. * It returns DO NOT KNOW with probability at mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |