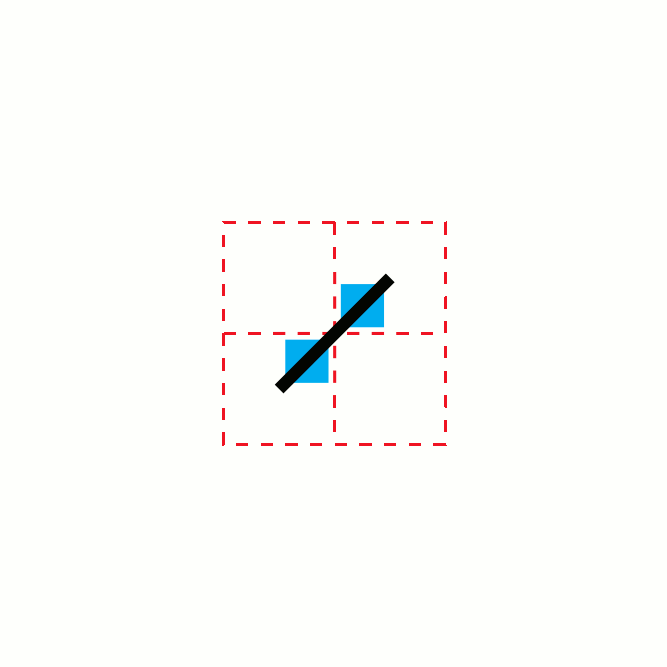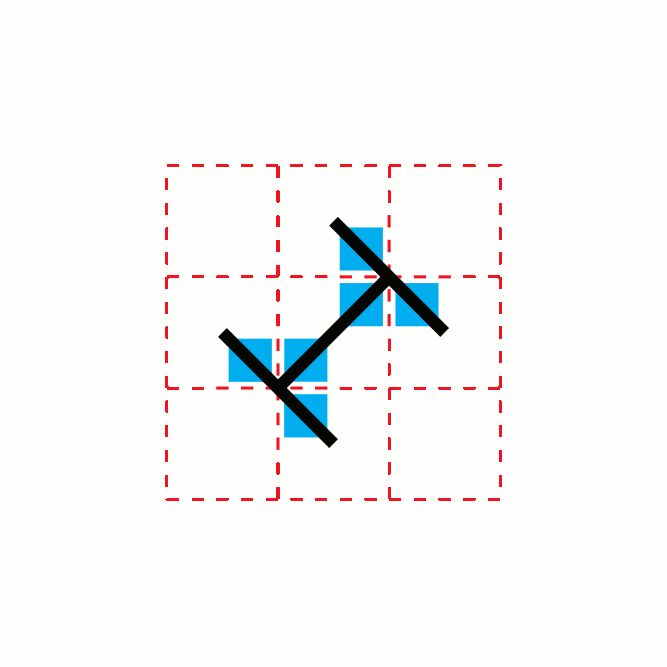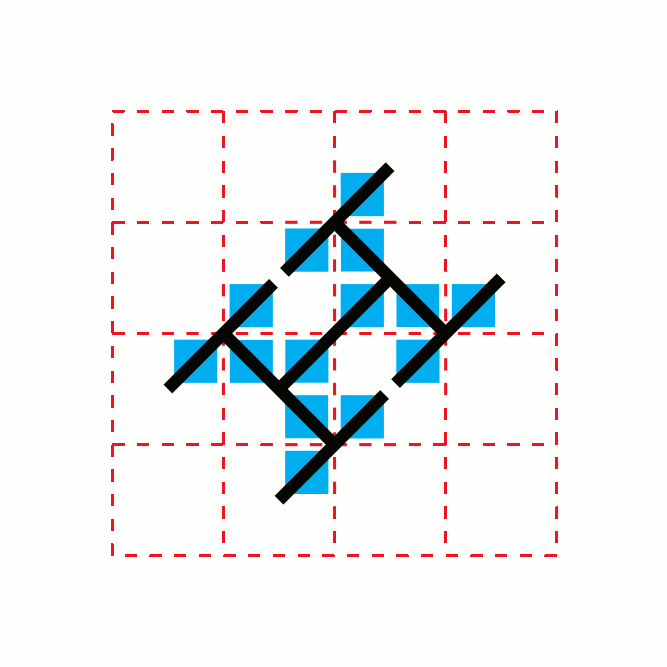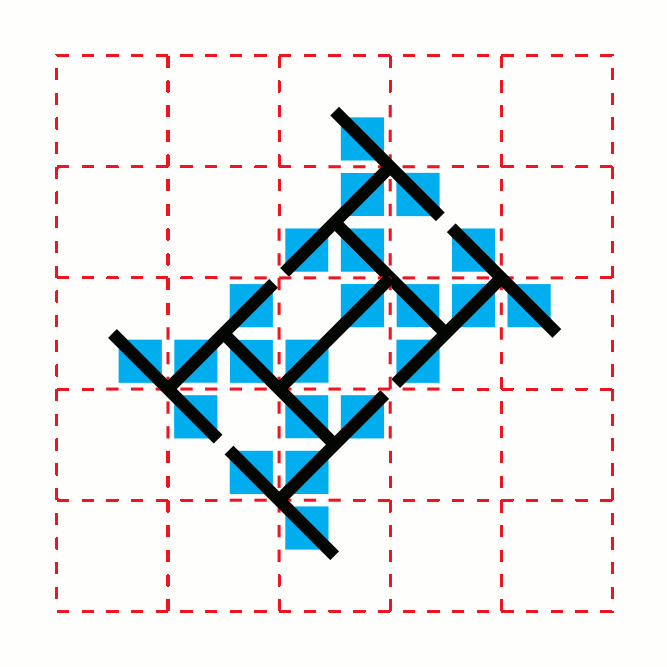|
Toothpick Sequence
In geometry, the toothpick sequence is a sequence of 2-dimensional patterns which can be formed by repeatedly adding line segments ("toothpicks") to the previous pattern in the sequence. The first stage of the design is a single "toothpick", or line segment. Each stage after the first is formed by taking the previous design and, for every exposed toothpick end, placing another toothpick centered at a right angle on that end. This process results in a pattern of growth in which the number of segments at stage oscillates with a fractal pattern between and . If denotes the number of segments at stage , then values of for which is near its maximum occur when is near a power of two, while the values for which it is near its minimum occur near numbers that are approximately times a power of two. The structure of stages in the toothpick sequence often resemble the T-square fractal, or the arrangement of cells in the Ulam–Warburton cellular automaton. All of the bounded region ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margolus Toothpick Animated
Margolus is a surname that, like its variants shown below, is derived from the Ashkenazi Hebrew pronunciation of the Hebrew word (Israeli Hebrew aɹgalit, meaning 'pearl,' and may refer to: *Norman Margolus, Canadian-American physicist and computer scientist See also * Margolis * Margolies * Margules * Margulies * Margulis * Margolin * Miriam Margolyes Miriam ( he, מִרְיָם ''Mīryām'', lit. 'Rebellion') is described in the Hebrew Bible as the daughter of Amram and Jochebed, and the older sister of Moses and Aaron. She was a prophetess and first appears in the Book of Exodus. The To ... * Margolius {{surname Jewish surnames Hebrew-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toothpick 89
A toothpick is a small thin stick of wood, plastic, bamboo, metal, bone or other substance with at least one and sometimes two pointed ends to insert between teeth to remove detritus, usually after a meal. Toothpicks are also used for festive occasions to hold or spear small appetizers (like cheese cubes or olives) or as a cocktail stick, and can be decorated with plastic frills or small paper umbrellas or flags. History Known in all cultures, the toothpick is the oldest instrument for dental cleaning. Hominin remains from Dmanisi, Georgia, dated to about 1.8 million years ago, bear lesions indicating the repeated use of a “toothpick”. A Neanderthal man's jawbone found in the Cova Foradà in Spain evidenced use of a toothpick to alleviate pain in his teeth caused by periodontal disease and dental wear. Toothpicks made of bronze have been found as burial objects in prehistoric graves in Northern Italy and in the East Alps. In 1986, researchers in Florida dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
T-square (fractal)
In mathematics, the T-square is a two-dimensional fractal. It has a boundary of infinite length bounding a finite area. Its name comes from the drawing instrument known as a T-square.Dale, Nell; Joyce, Daniel T.; and Weems, Chip (2016). ''Object-Oriented Data Structures Using Java'', p.187. Jones & Bartlett Learning. . "Our resulting image is a fractal called a T-square because with it we can see shapes that remind us of the technical drawing instrument of the same name." Algorithmic description It can be generated from using this algorithm: # Image 1: ## Start with a square. (The black square in the image) # Image 2: ## At each convex corner of the previous image, place another square, centered at that corner, with half the side length of the square from the previous image. ## Take the union of the previous image with the collection of smaller squares placed in this way. # Images 3–6: ## Repeat step 2. The method of creation is rather similar to the ones used to cre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ulam–Warburton Automaton
The Ulam–Warburton cellular automaton (UWCA) is a 2-dimensional fractal pattern that grows on a regular grid of cells consisting of squares. Starting with one square initially ON and all others OFF, successive iterations are generated by turning ON all squares that share precisely one edge with an ON square. This is the von Neumann neighborhood. The automaton is named after the Polish-American mathematician and scientist Stanislaw Ulam and the Scottish engineer, inventor and List of amateur mathematicians, amateur mathematician Mike Warburton. Properties and relations The UWCA is a 2D 5-neighbor outer totalistic cellular automaton using rule 686. The number of cells turned ON in each iteration is denoted u(n), with an explicit formula: u(0)=0, u(1)=1, and for n \ge 2 u(n) = 4\cdot 3^ where wt(n) is the Hamming weight function which counts the number of 1's in the binary expansion of n wt(n)=n-\sum_^ \left\lfloor\frac\right\rfloor The minimum upper bound of summation for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cellular Automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of '' states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that determines the new state ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them. Important examples Fermat's Last Theorem In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, ''b'', and ''c'' can satisfy the equation ''a^n + b^n = c^n'' for any integer value of ''n'' greater than two. This theorem was first conjectured by Pierre de Fermat in 1637 in the margin of a copy of ''Arithmetica'', where he claimed that he had a proof that was too large to fit in the margin. The first successful proof was released in 1994 by Andrew Wiles, and formally published in 1995, after 358 years of effort b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Of Two
A power of two is a number of the form where is an integer, that is, the result of exponentiation with number two as the base and integer as the exponent. In a context where only integers are considered, is restricted to non-negative values, so there are 1, 2, and 2 multiplied by itself a certain number of times. The first ten powers of 2 for non-negative values of are: : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, ... Because two is the base of the binary numeral system, powers of two are common in computer science. Written in binary, a power of two always has the form 100...000 or 0.00...001, just like a power of 10 in the decimal system. Computer science Two to the exponent of , written as , is the number of ways the bits in a binary word of length can be arranged. A word, interpreted as an unsigned integer, can represent values from 0 () to () inclusively. Corresponding signed integer values can be positive, negative and zero; see signe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
On-line Encyclopedia Of Integer Sequences
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is chairman of the OEIS Foundation. OEIS records information on integer sequences of interest to both professional and amateur mathematicians, and is widely cited. , it contains over 350,000 sequences, making it the largest database of its kind. Each entry contains the leading terms of the sequence, keywords, mathematical motivations, literature links, and more, including the option to generate a graph or play a musical representation of the sequence. The database is searchable by keyword, by subsequence, or by any of 16 fields. History Neil Sloane started collecting integer sequences as a graduate student in 1965 to support his work in combinatorics. The database was at first stored on punche ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brian Hayes (scientist)
Brian Hayes (born 10 December 1949) is an American scientist, columnist and author. He is a senior writer and regular columnist for the magazine '' American Scientist'', and was editor in chief for the magazine from 1990 to 1992. He has also edited and written columns for ''Scientific American'', as well as writing for ''Computer Language'' and ''The Sciences''. He won a National Magazine Award The National Magazine Awards, also known as the Ellie Awards, honor print and digital publications that consistently demonstrate superior execution of editorial objectives, innovative techniques, noteworthy enterprise and imaginative design. Or ... for his essay "Clock of Ages" in 2000. He is the author of three books: *''Infrastructure: A Field Guide to the Industrial Landscape'' (W. W. Norton, 2005, ; revised and updated edition: W.W. Norton, 2014, ). *''Group Theory in the Bedroom, and Other Mathematical Diversions'' (Hill and Wang, 2008; Macmillan, 2009, ).. *''Foolproof, and Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cellular Automaton Patterns
Cellular may refer to: *Cellular automaton, a model in discrete mathematics *Cell biology, the evaluation of cells work and more * ''Cellular'' (film), a 2004 movie *Cellular frequencies, assigned to networks operating in cellular RF bands *Cellular manufacturing *Cellular network, cellular radio networks * U.S. Cellular Field, also known as "The Cell", a baseball stadium in Chicago * U.S. Cellular Arena, an arena in Milwaukee, Wisconsin Terms such as cellular organization, cellular structure, cellular system, and so on may refer to: *Cell biology, the evaluation of how cells work and more *Cellular communication networks, systems for allowing communication through mobile phones and other mobile devices *Cellular organizational structures, methods of human organization in social groups *Clandestine cell organizations, entities organized to commit crimes, acts of terror, or other malicious activities See also *Cell (other) Cell most often refers to: * Cell (biology), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |