Toothpick Sequence on:
[Wikipedia]
[Google]
[Amazon]
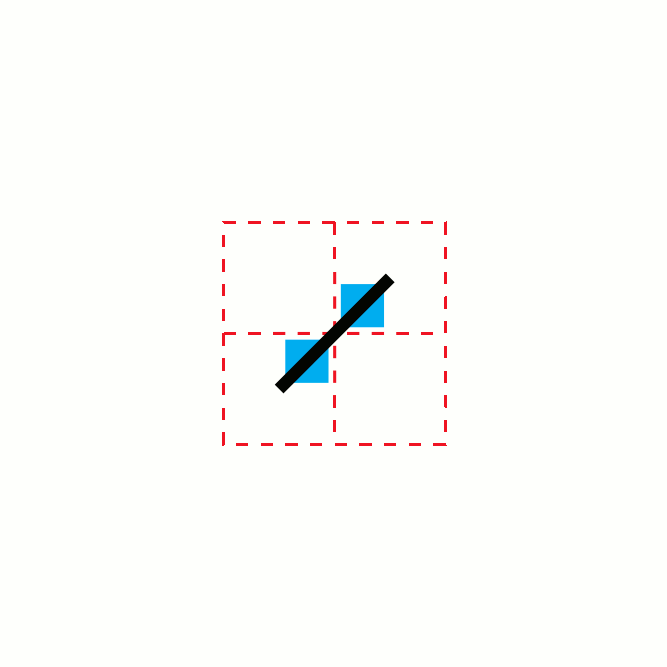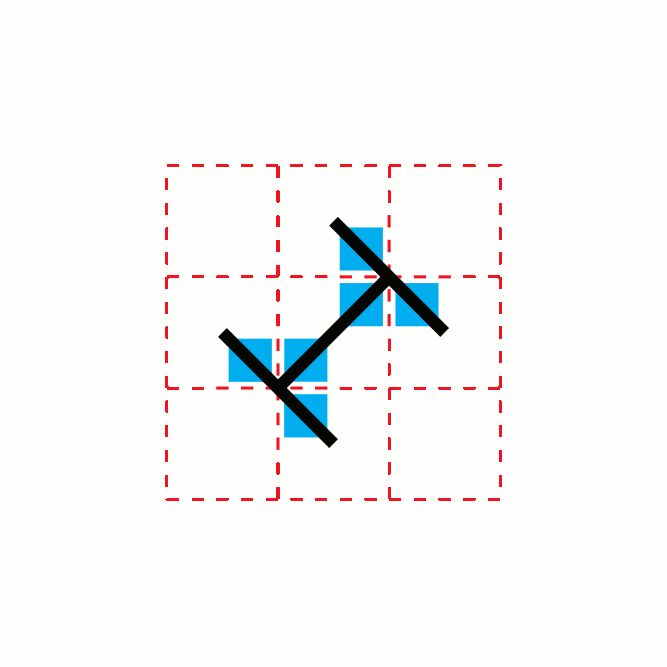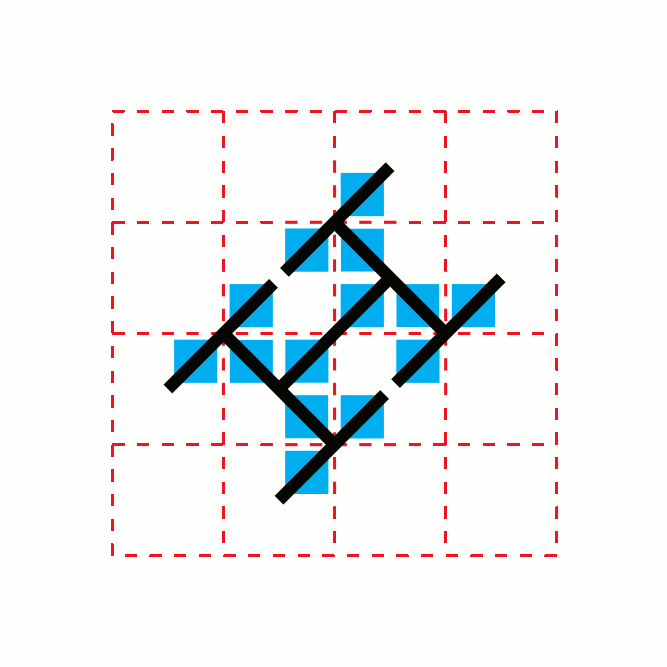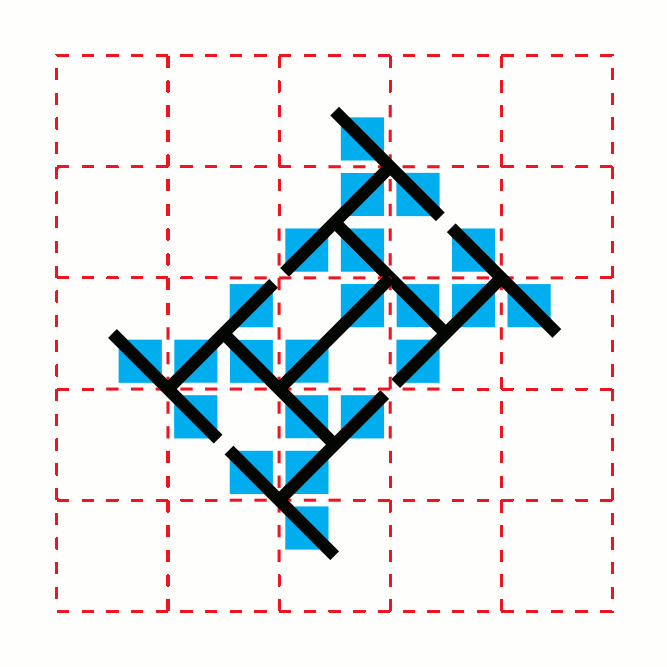
 In
In
A list of integer sequences related to the Toothpick Sequence
from the
search page
)
Joshua Trees and Toothpicks
Brian Hayes, 8 February 2013 Cellular automaton patterns Combinatorics
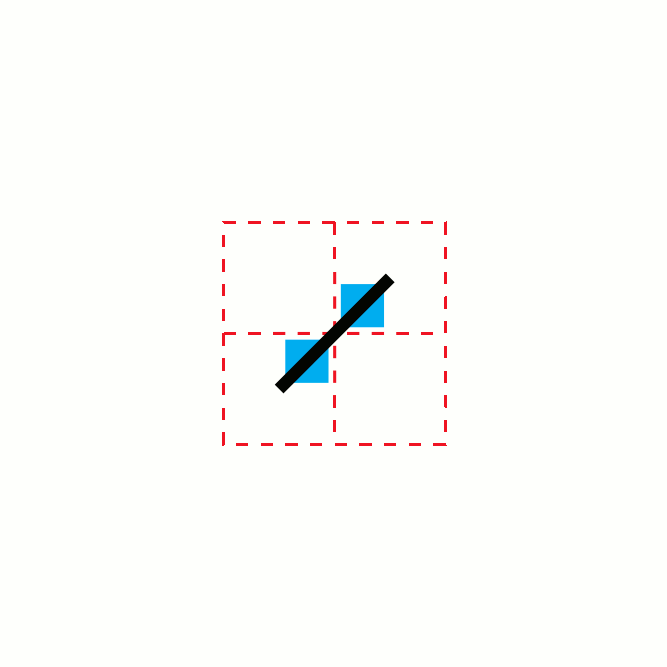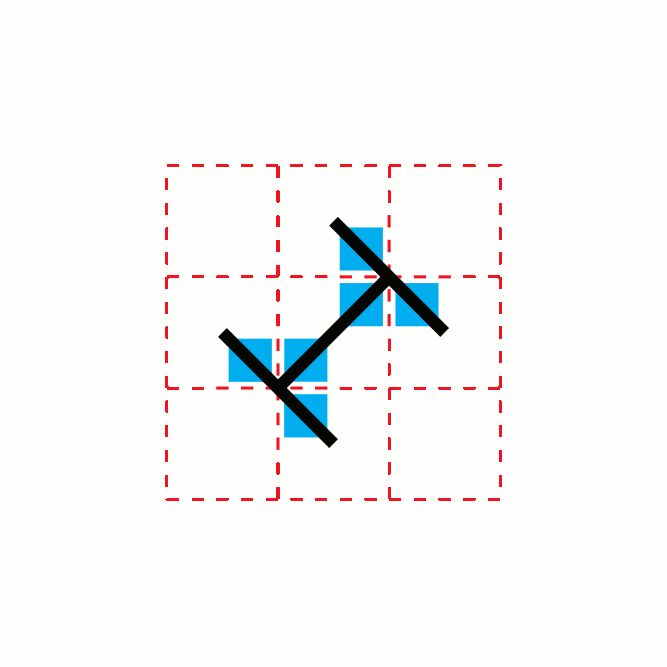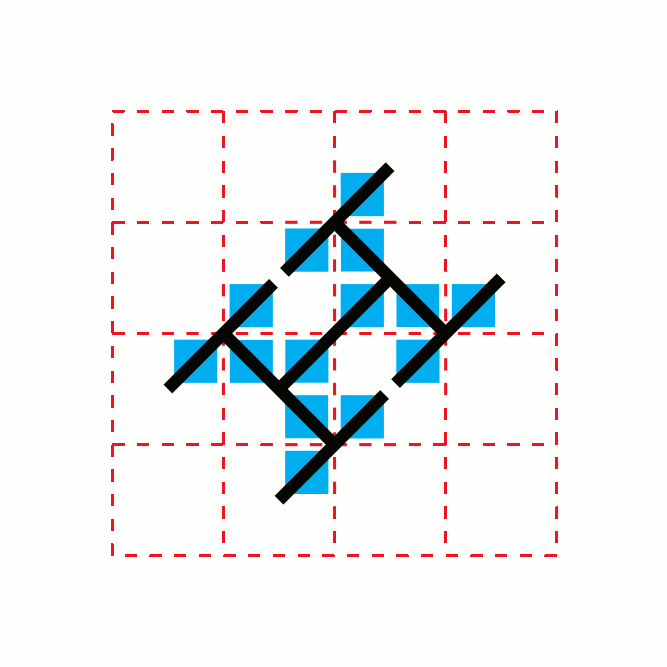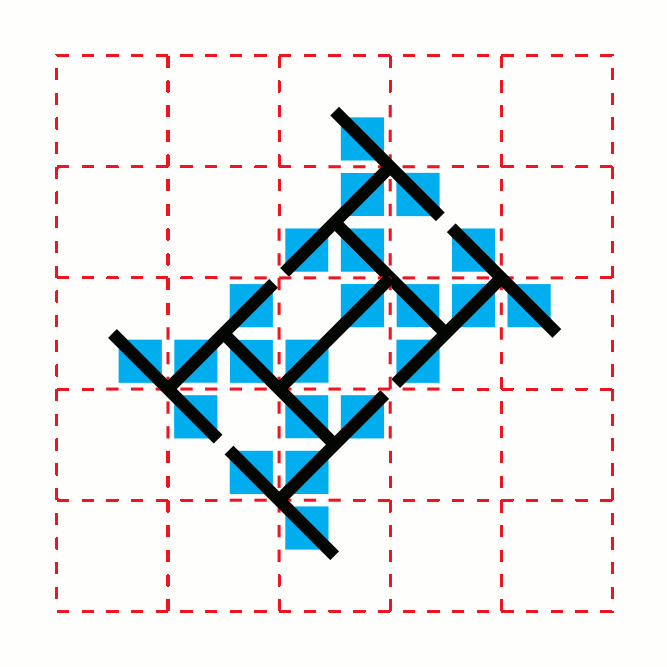
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, the toothpick sequence is a sequence of 2-dimensional patterns which can be formed by repeatedly adding line segments ("toothpicks") to the previous pattern in the sequence.
The first stage of the design is a single "toothpick", or line segment. Each stage after the first is formed by taking the previous design and, for every exposed toothpick end, placing another toothpick centered at a right angle on that end.
This process results in a pattern of growth in which the number of segments at stage oscillates with a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as il ...
pattern between and . If denotes the number of segments at stage , then values of for which is near its maximum occur when is near a power of two, while the values for which it is near its minimum occur near numbers that are approximately times a power of two. The structure of stages in the toothpick sequence often resemble the T-square
A T-square is a technical drawing instrument used by draftsmen primarily as a guide for drawing horizontal lines on a drafting table. The instrument is named after its resemblance to the letter T, with a long shaft called the "blade" and a sh ...
fractal, or the arrangement of cells in the Ulam–Warburton cellular automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tess ...
.
All of the bounded regions surrounded by toothpicks in the pattern, but not themselves crossed by toothpicks, must be squares or rectangles. It has been conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 1 ...
d that every open rectangle in the toothpick pattern (that is, a rectangle that is completely surrounded by toothpicks, but has no toothpick crossing its interior) has side lengths and areas that are powers of two
A power of two is a number of the form where is an integer, that is, the result of exponentiation with number two as the base and integer as the exponent.
In a context where only integers are considered, is restricted to non-negative ...
, with one of the side lengths being at most two.
References
{{ReflistExternal links
A list of integer sequences related to the Toothpick Sequence
from the
On-line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to ...
. (note: IDs such as ''A139250'' are IDs within the OEIS, and descriptions of the sequences can be located by entering these IDs in the OEIsearch page
)
Joshua Trees and Toothpicks
Brian Hayes, 8 February 2013 Cellular automaton patterns Combinatorics