|
Tone System
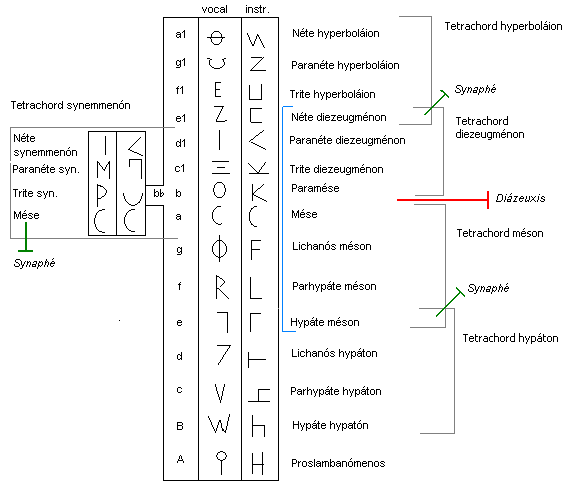
The musical system of ancient Greece evolved over a period of more than 500 years from simple scales of tetrachords, or divisions of the perfect fourth, into several complex systems encompassing tetrachords and octaves, as well as octave scales divided into seven to thirteen intervals. Any discussion of the music of ancient Greece, theoretical, philosophical or aesthetic, is fraught with two problems: there are few examples of written music, and there are many, sometimes fragmentary, theoretical and philosophical accounts. The empirical research of scholars like Richard Crocker, C. André Barbera, and John Chalmers has made it possible to look at the ancient Greek systems as a whole without regard to the tastes of any one ancient theorist. The primary genera they examine are those of Pythagoras and the Pythagorean school, Archytas, Aristoxenos, and Ptolemy (including his versions of the genera of Didymos and Eratosthenes). Overview of the first complete tone system As an init ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale (music)
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale. Often, especially in the context of the common practice period, most or all of the melody and harmony of a musical work is built using the notes of a single scale, which can be conveniently represented on a staff with a standard key signature. Due to the principle of octave equivalence, scales are generally considered to span a single octave, with higher or lower octaves simply repeating the pattern. A musical scale represents a division of the octave space into a certain number of scale steps, a scale step being the recognizable distance (or interval) between two successive notes of the scale. However, there is no need for scale steps to be equal within any scale and, particularly as demonstrated by microtonal music, there is no limit to how many notes can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave Species
In the musical system of ancient Greece, an octave species (εἶδος τοῦ διὰ πασῶν, or σχῆμα τοῦ διὰ πασῶν) is a specific sequence of intervals within an octave. In ''Elementa harmonica'', Aristoxenus classifies the species as three different genera, distinguished from each other by the largest intervals in each sequence: the diatonic, chromatic, and enharmonic genera, whose largest intervals are, respectively, a whole tone, a minor third, and a ditone; quarter tones and semitones complete the tetrachords. The concept of octave species is very close to tonoi and akin to musical scale and mode, and was invoked in Medieval and Renaissance theory of Gregorian mode and Byzantine Octoechos. Ancient Greek theory Greek theorists used two terms interchangeably to describe what we call species: ''eidos'' (εἶδος) and ''skhēma'' (σχῆμα), defined as "a change in the arrangement of incomposite ntervalsmaking up a compound magnitude while ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of philosophy within the Lyceum and the wider Aristotelian tradition. His writings cover many subjects including physics, biology, zoology, metaphysics, logic, ethics, aesthetics, poetry, theatre, music, rhetoric, psychology, linguistics, economics, politics, meteorology, geology, and government. Aristotle provided a complex synthesis of the various philosophies existing prior to him. It was above all from his teachings that the West inherited its intellectual lexicon, as well as problems and methods of inquiry. As a result, his philosophy has exerted a unique influence on almost every form of knowledge in the West and it continues to be a subject of contemporary philosophical discussion. Little is known about his life. Aristotle was born in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristoxenos
Aristoxenus of Tarentum ( el, Ἀριστόξενος ὁ Ταραντῖνος; born 375, fl. 335 BC) was a Greek Peripatetic philosopher, and a pupil of Aristotle. Most of his writings, which dealt with philosophy, ethics and music, have been lost, but one musical treatise, ''Elements of Harmony'' (Greek: Ἁρμονικὰ στοιχεῖα; Latin: ''Elementa harmonica''), survives incomplete, as well as some fragments concerning rhythm and meter. The ''Elements'' is the chief source of our knowledge of ancient Greek music."Aristoxenus of Tarentum" in ''Chambers's Encyclopædia''. London: George Newnes, 1961, Vol. 1, p. 593. Life Aristoxenus was born at Tarentum, and was the son of a learned musician named Spintharus (otherwise Mnesias). He learned music from his father, and having then been instructed by Lamprus of Erythrae and Xenophilus the Pythagorean, he finally became a pupil of Aristotle, whom he appears to have rivaled in the variety of his studies. According to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enharmonic Genus
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Genus
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Genus
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Second
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two commonly occurring thirds. It is called ''minor'' because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The minor third is a skip melodically. Notable examples of ascending minor thirds include the opening two notes of " Greensleeves" and of " Light My Fire". The minor third may be derived from the harmonic series as the interval between the fifth and sixth harmonics, or from the 19th harmonic. The minor third is co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (music)
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved new innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus (mathematician), Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the philosophers Proclus and Pappus of Alexandria many centuries later. Until the early Renaissance he was often mistaken f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |