|
Genus (music)
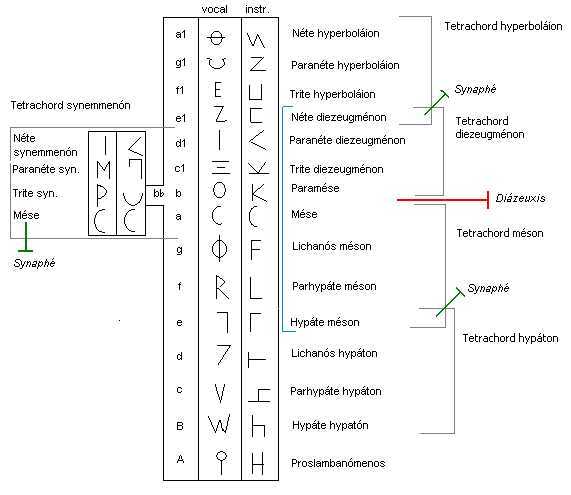
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical System Of Ancient Greece
The musical system of ancient Greece evolved over a period of more than 500 years from simple scales of tetrachords, or divisions of the perfect fourth, into several complex systems encompassing tetrachords and octaves, as well as octave scales divided into seven to thirteen intervals. Any discussion of the music of ancient Greece, theoretical, philosophical or aesthetic, is fraught with two problems: there are few examples of written music, and there are many, sometimes fragmentary, theoretical and philosophical accounts. The empirical research of scholars like Richard Crocker, C. André Barbera, and John Chalmers has made it possible to look at the ancient Greek systems as a whole without regard to the tastes of any one ancient theorist. The primary genera they examine are those of Pythagoras and the Pythagorean school, Archytas, Aristoxenos, and Ptolemy (including his versions of the genera of Didymos and Eratosthenes). Overview of the first complete tone system As an init ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are Maximal evenness, maximally separated from each other (i.e. separated by at least two whole steps). The seven pitch (music), pitches of any diatonic scale can also be obtained by using a Interval cycle, chain of six perfect fifths. For instance, the seven natural (music), natural pitch classes that form the C-major scale can be obtained from a stack of perfect fifths starting from F: :F–C–G–D–A–E–B Any sequence of seven successive natural notes, such as C–D–E–F–G–A–B, and any Transposition (music), transposition thereof, is a diatonic scale. Modern musical keyboards are des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Tetrachord Pythagorean Tuning
Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900. These terms may mean different things in different contexts. Very often, ''diatonic'' refers to musical elements derived from the modes and transpositions of the "white note scale" C–D–E–F–G–A–B. In some usages it includes all forms of heptatonic scale that are in common use in Western music (the major, and all forms of the minor). ''Chromatic'' most often refers to structures derived from the twelve-note chromatic scale, which consists of all semitones. Historically, however, it had other senses, referring in Ancient Greek music theory to a particular tuning of the tetrachord, and to a rhythmic notational convention in me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genesis Of A Music
''Genesis of a Music'' is a book first published in 1949 by microtonal composer Harry Partch (1901–1974). Partch first presents a polemic against both equal temperament and the long history of stagnation in the teaching of music; according to Alex Ross, this is "the most startling forty-five-page history of music ever written". In particular, Partch holds Johann Sebastian Bach responsible for "the movement toward equal-tempered tuning, which meant that composers could not absorb the scales of other world traditions; and the urge to make music ever more instrumental and abstract." He then goes on to explain his tuning theory based on just intonation, the ensemble of musical instruments of his own invention (such as the "Surrogate Kithara, a struck-string, harplike instrument", and the guitar with movable frets he used to compose ''Barstow''), and several of his largest musical compositions. The book has been highly influential to succeeding generations of microtonal composers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harry Partch
Harry Partch (June 24, 1901 – September 3, 1974) was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century composers in the West to work systematically with microtonal scales, alongside Lou Harrison. He built custom-made instruments in these tunings on which to play his compositions, and described the method behind his theory and practice in his book '' Genesis of a Music'' (1947). Partch composed with scales dividing the octave into 43 unequal tones derived from the natural harmonic series; these scales allowed for more tones of smaller intervals than in standard Western tuning, which uses twelve equal intervals to the octave. To play his music, Partch built many unique instruments, with such names as the Chromelodeon, the Quadrangularis Reversum, and the Zymo-Xyl. Partch described his music as corporeal, and distinguished it from abs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Pachymeres
George Pachymeres ( el, Γεώργιος Παχυμέρης, Geórgios Pachyméris; 1242 – 1310) was a Byzantine Greek historian, philosopher, music theorist and miscellaneous writer. Biography Pachymeres was born at Nicaea, in Bithynia, where his father had taken refuge after the capture of Constantinople by the Latins in 1204. Upon the recovery of Constantinople from the Latin Empire by Michael VIII Palaeologus, Pachymeres settled there, studied law, entered the church, and subsequently became chief advocate of the church and chief justice of the imperial court. His literary activity was considerable, his most important work being a Byzantine history in thirteen books, in continuation of that of George Acropolites from 1261 to 1308, containing the history of the reigns of Michael and Andronicus II Palaeologus. Pachymeres was also the author of rhetorical exercises on philosophical themes; of a ''Quadrivium'' (arithmetic, music, geometry, astronomy), valuable for the history ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as the differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditone
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third. Pythagorean tuning The Pythagorean ditone is the major third in Pythagorean tuning, which has an interval ratio of 81:64, which is 407.82 cents. The Pythagorean ditone is evenly divisible by two major tones (9/8 or 203.91 cents) and is wider than a just major third (5/4, 386.31 cents) by a syntonic comma (81/80, 21.51 cents). Because it is a comma wider than a "perfect" major third of 5:4, it is called a "comma-redundant" interval. "The major third that appears commonly in the ythagoreansystem (C–E, D–F, etc.) is more properly known as the Pythagorean ditone and consists of two major and two minor semit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers. For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |