|
Thermal Entrance Length
In fluid dynamics, the entrance length is the distance a flow travels after entering a pipe before the flow becomes fully developed.''ES162_08_Notes02a_Flow_In_Pipes_Changtamu.Pdf''. 1st ed. Cambridge: J. R. Rice, 2017. Print. Entrance length refers to the length of the entry region, the area following the pipe entrance where effects originating from the interior wall of the pipe propagate into the flow as an expanding boundary layer. When the boundary layer expands to fill the entire pipe, the developing flow becomes a fully developed flow, where flow characteristics no longer change with increased distance along the pipe. Many different entrance lengths exist to describe a variety of flow conditions. Hydrodynamic entrance length describes the formation of a velocity profile caused by viscous forces propagating from the pipe wall. Thermal entrance length describes the formation of a temperature profile. Awareness of entrance length may be necessary for the effective placement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and time. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
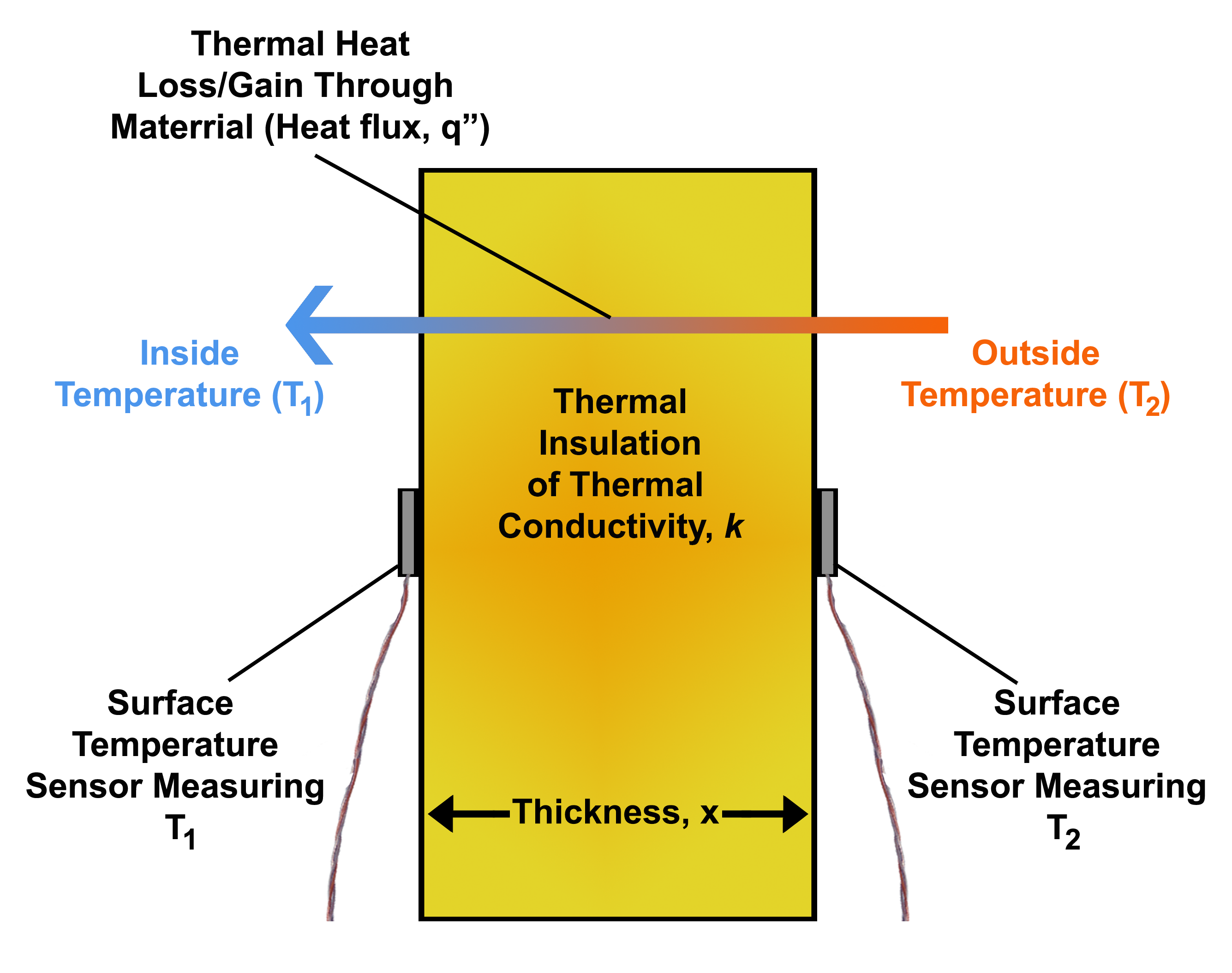
Heat Flux
Heat flux or thermal flux, sometimes also referred to as ''heat flux density'', heat-flow density or ''heat flow rate intensity'' is a flow of energy per unit area per unit time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''mass'' or ''momentum'' flux. Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi_\text = -k \frac where k is the thermal conductivity. The negative sign shows that heat flux moves from higher temperature regions to lower temperature regions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schmidt Number
Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975). The Schmidt number is the ratio of the shear component for diffusivity ''viscosity/density'' to the diffusivity for mass transfer ''D''. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer. It is defined as: :\mathrm = \frac = \frac = \frac where: * \nu is the kinematic viscosity or (/\,) in units of (m2/s) * D is the mass diffusivity (m2/s). * is the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/m·s) * \rho is the density of the fluid (kg/m3). The heat transfer analog of the Schmidt number is the Prandtl number (Pr). The ratio of thermal diffusivity to mass diffusivity is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', ''molar concentration'', ''number concentration'', and ''volume concentration''. The concentration can refer to any kind of chemical mixture, but most frequently refers to solutes and solvents in solutions. The molar (amount) concentration has variants, such as normal concentration and osmotic concentration. Etymology The term concentration comes from the word concentrate, from the French , from con– + center, meaning “to put at the center”. Qualitative description Often in informal, non-technical language, concentration is described in a qualitative way, through the use of adjectives such as "dilute" for solutions of relatively low concentration and "concentrated" for solutions of relatively high concentration. To concentrate a solution, one must add more solute (for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection (heat Transfer)
Convection (or convective heat transfer) is the transfer of heat from one place to another due to the movement of fluid. Although often discussed as a distinct method of heat transfer, convective heat transfer involves the combined processes of conduction (heat diffusion) and advection (heat transfer by bulk fluid flow). Convection is usually the dominant form of heat transfer in liquids and gases. Note that this definition of convection is only applicable in Heat transfer and thermodynamic contexts. It should not to be confused with the dynamic fluid phenomenon of convection, which is typically referred to as ''Natural Convection'' in thermodynamic contexts in order to distinguish the two. Overview Convection can be "forced" by movement of a fluid by means other than buoyancy forces (for example, a water pump in an automobile engine). Thermal expansion of fluids may also force convection. In other cases, natural buoyancy forces alone are entirely responsible for fluid mot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steam
Steam is a substance containing water in the gas phase, and sometimes also an aerosol of liquid water droplets, or air. This may occur due to evaporation or due to boiling, where heat is applied until water reaches the enthalpy of vaporization. Steam that is saturated or superheated is invisible; however, "steam" often refers to wet steam, the visible mist or aerosol of water droplets formed as water vapor condenses. Water increases in volume by 1,700 times at standard temperature and pressure; this change in volume can be converted into mechanical work by steam engines such as reciprocating piston type engines and steam turbines, which are a sub-group of steam engines. Piston type steam engines played a central role in the Industrial Revolution and modern steam turbines are used to generate more than 80% of the world's electricity. If liquid water comes in contact with a very hot surface or depressurizes quickly below its vapor pressure, it can create a steam explosion. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensation
Condensation is the change of the state of matter from the gas phase into the liquid phase, and is the reverse of vaporization. The word most often refers to the water cycle. It can also be defined as the change in the state of water vapor to liquid water when in contact with a liquid or solid surface or cloud condensation nuclei within the atmosphere. When the transition happens from the gaseous phase into the solid phase directly, the change is called deposition. Initiation Condensation is initiated by the formation of atomic/molecular clusters of that species within its gaseous volume—like rain drop or snow flake formation within clouds—or at the contact between such gaseous phase and a liquid or solid surface. In clouds, this can be catalyzed by water-nucleating proteins, produced by atmospheric microbes, which are capable of binding gaseous or liquid water molecules. Reversibility scenarios A few distinct reversibility scenarios emerge here with respect to the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joule Heating
Joule heating, also known as resistive, resistance, or Ohmic heating, is the process by which the passage of an electric current through a conductor (material), conductor produces heat. Joule's first law (also just Joule's law), also known in countries of former Soviet Union, USSR as the Joule–Lenz law, Assuming the element behaves as a perfect resistor and that the power is completely converted into heat, the formula can be re-written by substituting Ohm's law, V = I R , into the generalized power equation: P = IV = I^2R = V^2/R where ''R'' is the electrical resistance and conductance, resistance. Alternating current When current varies, as it does in AC circuits, P(t) = U(t) I(t) where ''t'' is time and ''P'' is the instantaneous power being converted from electrical energy to heat. Far more often, the ''average'' power is of more interest than the instantaneous power: P_ = U_\text I_\text = I_\text^2 R = U_\text^2 / R where "avg" denotes Arithmetic mean, average (mean) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It measures the rate of transfer of heat of a material from the hot end to the cold end. It has the SI derived unit of m2/s. Thermal diffusivity is usually denoted by lowercase alpha (), but , , ( kappa), , and are also used. The formula is: :\alpha = \frac where * is thermal conductivity (W/(m·K)) * is specific heat capacity (J/(kg·K)) * is density (kg/m3) Together, can be considered the volumetric heat capacity (J/(m3·K)). As seen in the heat equation, :\frac = \alpha \nabla^2 T, one way to view thermal diffusivity is as the ratio of the time derivative of temperature to its curvature, quantifying the rate at which temperature concavity is "smoothed out". In a sense, thermal diffusivity is a contrasting measure to thermal inertia. In a substance with high thermal diffusivity, heat moves rapidly through it because the substa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Quantity
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the field of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as: : \mathrm = \frac = \frac = \frac = \frac where: * \nu : momentum diffusivity (kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |