|
Sinusoidal Projection
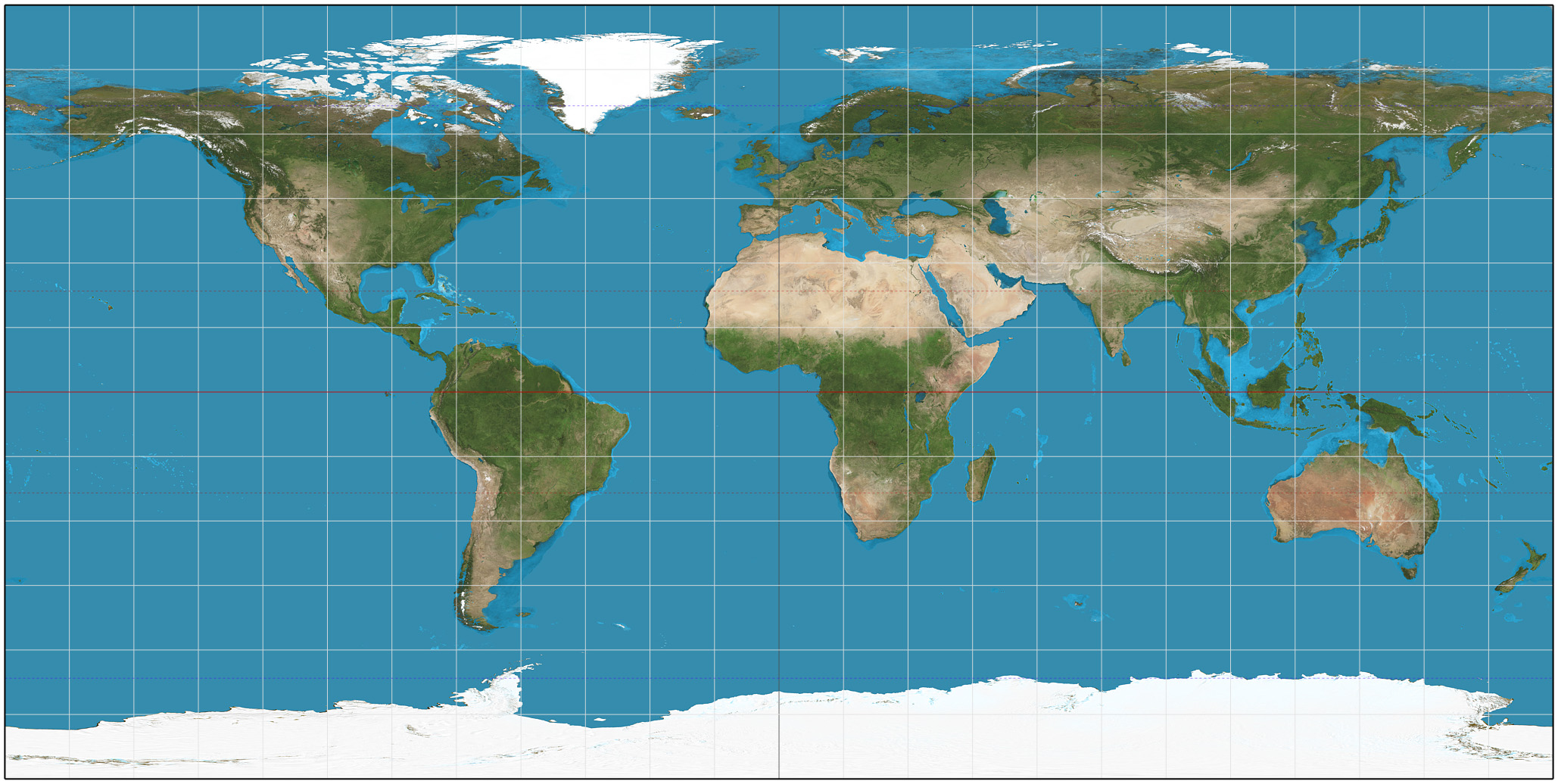
The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, using it in a world map in 1570. The projection represents the poles as points, as they are on the sphere, but the meridians and continents are distorted. The equator and the central meridian are the most accurate parts of the map, having no distortion at all, and the further away from those that one examines, the greater the distortion. The projection is defined by: :\begin x &= \left(\lambda - \lambda_0\right) \cos \varphi \\ y &= \varphi\,\end where \varphi is the latitude, ''λ'' is the longitude, and ''λ'' is the longitude of the central meridian. Scale is constant along the central meridian, and east–west scale is constant throughout the map. Therefore, the length of each parallel on the map is proportional to the cosine of the latitude, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sinusoidal Projection SW
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the ''sine'' and ''cosine'' component ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
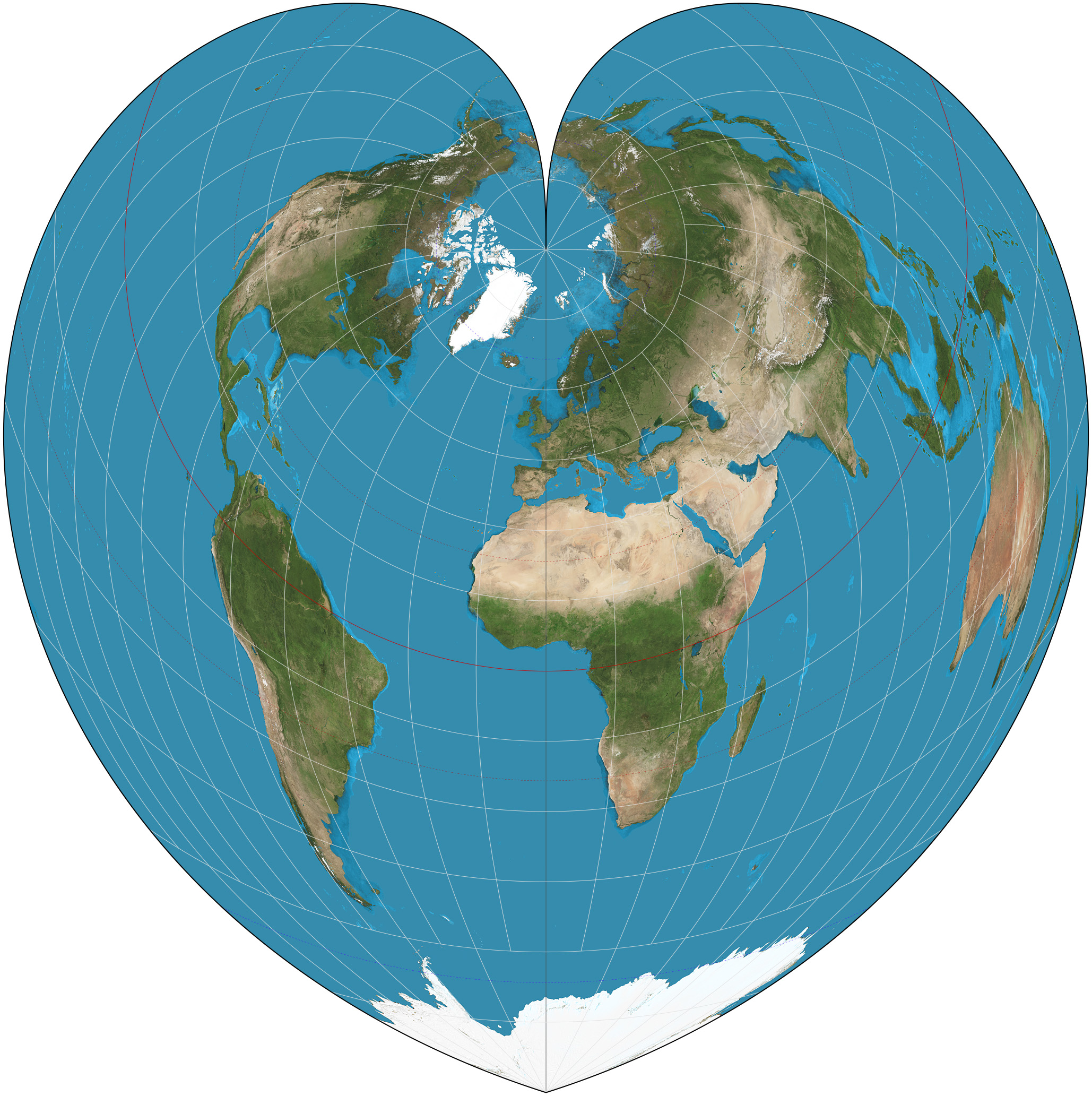
Werner Projection
The Werner projection is a pseudoconic equal-area map projection sometimes called the Stab-Werner or Stabius-Werner projection. Like other heart-shaped projections, it is also categorized as cordiform. ''Stab-Werner'' refers to two originators: Johannes Werner (1466–1528), a parish priest in Nuremberg, refined and promoted this projection that had been developed earlier by Johannes Stabius (Stab) of Vienna Vienna ( ; ; ) is the capital city, capital, List of largest cities in Austria, most populous city, and one of Federal states of Austria, nine federal states of Austria. It is Austria's primate city, with just over two million inhabitants. ... around 1500. The projection is a limiting form of the Bonne projection, having its standard parallel at one of the poles (90°N/S).. Distances along each parallel and along the central meridian are correct, as are all distances from the north pole. See also * List of map projections References External links * *. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nicolas Sanson
Nicolas Sanson (20 December 1600 – 7 July 1667) was a French cartographer who served under two kings in matters of geography. He has been called the "father of French cartography." Life and work He was born of an old Picardy, Picard family of Scotland, Scottish descent, at Abbeville, on 20 (or 31) December 1600, and was educated by the Jesuits at Amiens. In 1627 he attracted the attention of Cardinal Richelieu, Richelieu by a map of Gaul which he had constructed (or at least begun) while only eighteen. Sanson was royal geographer. He gave lessons in geography both to Louis XIII of France, Louis XIII and to Louis XIV of France, Louis XIV; and when Louis XIII, it is said, came to Abbeville, he preferred to be the guest of Sanson (then employed on the fortifications), instead of occupying the lodgings provided by the town. At the conclusion of this visit the king made Sanson a councillor of state. Active from 1627, Sanson issued his first map of importance, the "Postes de Fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gerardus Mercator
Gerardus Mercator (; 5 March 1512 – 2 December 1594) was a Flemish people, Flemish geographer, cosmographer and Cartography, cartographer. He is most renowned for creating the Mercator 1569 world map, 1569 world map based on a new Mercator projection, projection which represented sailing courses of constant bearing (rhumb lines) as straight lines—an innovation that is still employed in nautical charts. Mercator was a notable maker of globes and scientific instruments. In addition, he had interests in theology, philosophy, history, mathematics, and geomagnetism. He was also an accomplished engraving, engraver and Calligraphy, calligrapher. Unlike other great scholars of the age, he travelled little and his knowledge of geography came from his library of over a thousand books and maps, from his visitors and from his vast correspondence (in six languages) with other scholars, statesmen, travellers, merchants and seamen. Mercator's early maps were in large formats suitable for w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
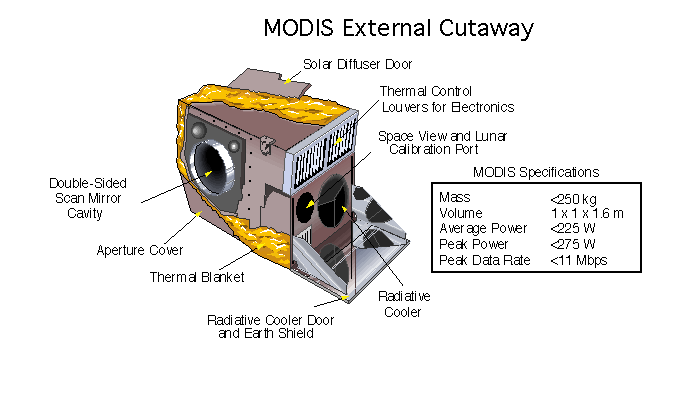
MODIS
The Moderate Resolution Imaging Spectroradiometer (MODIS) is a satellite-based sensor used for earth and climate measurements. There are two MODIS sensors in Earth orbit: one on board the Terra (EOS AM) satellite, launched by NASA in 1999; and one on board the Aqua (EOS PM) satellite, launched in 2002. Since 2011, MODIS operations have been supplemented by VIIRS sensors, such as the one aboard Suomi NPP. The systems often conduct similar operations due to their similar designs and orbits (with VIIRS data systems deisgned to be compatible with MODIS), though they have subtle differences contributing to similar but not identical uses. The MODIS instruments were built by Santa Barbara Remote Sensing. They capture data in 36 spectral bands ranging in wavelength from 0.4 μm to 14.4 μm and at varying spatial resolutions (2 bands at 250 m, 5 bands at 500 m and 29 bands at 1 km). Together the instruments image the entire Earth every 1 to 2 days. They are designed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Moderate-Resolution Imaging Spectroradiometer
The Moderate Resolution Imaging Spectroradiometer (MODIS) is a satellite-based sensor used for earth and climate measurements. There are two MODIS sensors in Geocentric orbit, Earth orbit: one on board the Terra (satellite), Terra (Earth Observing System, EOS AM) satellite, launched by NASA in 1999; and one on board the Aqua (satellite), Aqua (EOS PM) satellite, launched in 2002. Since 2011, MODIS operations have been supplemented by VIIRS sensors, such as the one aboard Suomi NPP. The systems often conduct similar operations due to their similar designs and orbits (with VIIRS data systems deisgned to be compatible with MODIS), though they have subtle differences contributing to similar but not identical uses. The MODIS instruments were built by Santa Barbara Remote Sensing. They capture data in 36 spectral bands ranging in wavelength from 0.4 μm to 14.4 μm and at varying spatial resolutions (2 bands at 250 m, 5 bands at 500 m and 29 bands at 1 km). Together th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geodesic Grid
A geodesic grid is a spatial grid based on a geodesic polyhedron or Goldberg polyhedron. History The earliest use of the (icosahedral) geodesic grid in geophysical modeling dates back to 1968 and the work by Sadourny, Arakawa, and Mintz and Williamson. Later work expanded on this base. Construction A geodesic grid is a global Earth spatial reference that uses polygon tiles based on the subdivision of a polyhedron (usually the icosahedron, and usually a Class I subdivision) to subdivide the surface of the Earth. Such a grid does not have a straightforward relationship to latitude and longitude, but conforms to many of the main criteria for a statistically valid discrete global grid. Primarily, the cells' area and shape are generally similar, especially near the poles where many other spatial grids have singularities or heavy distortion. The popular Quaternary Triangular Mesh (QTM) falls into this category. Geodesic grids may use the dual polyhedron of the geodesic polyhedron, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bottomley Projection
The Bottomley map projection is a pseudoconical equal area map projection defined as: :x = \frac, \qquad y = \frac - \rho \cos E \, where :\rho = \frac - \varphi, \qquad E = \frac and ''φ'' is the latitude, ''λ'' is the longitude from the central meridian, and ''φ''1 is the given parallel of the projection which determines its shape, all in radians. The inverse projection is then given by: :\begin\varphi &= \frac - \rho \\ \lambda &=\frac \end where :\rho = \sqrt, \qquad E= \tan^\left(\frac\right). Parallels (i.e. lines of latitude) are concentric elliptical arcs of constant eccentricity equal to cos ''φ''1, centred on the North Pole. On the central meridian, shapes are not distorted, but elsewhere they are. Different projections can be produced by altering the eccentricity of the arcs, making it vary between the sinusoidal projection and the Werner projection. For larger values of ''φ''1, it produces a heart shape. It was introduced by Henry Bottomley as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bonne Projection
The Bonne projection is a pseudoconical equal-area map projection, sometimes called a dépôt de la guerre, modified Flamsteed, or a Sylvanus projection. Although named after Rigobert Bonne (1727–1795), the projection was in use prior to his birth, by Sylvanus in 1511, Honter in 1561, De l'Isle before 1700 and Coronelli in 1696. Both Sylvanus and Honter's usages were approximate, however, and it is not clear they intended to be the same projection. The Bonne projection maintains accurate shapes of areas along the central meridian and the standard parallel, but progressively distorts away from those regions. Thus, it best maps "t"-shaped regions. It has been used extensively for maps of Europe and Asia. The projection is defined as: :\begin x &= \rho \sin E \\ y &= \cot \varphi_1 - \rho \cos E\end where :\begin\rho &= \cot \varphi_1 + \varphi_1 - \varphi \\ E &= \frac \end and ''φ'' is the latitude, ''λ'' is the longitude, ''λ''0 is the longitude of the central me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's rotation, Earth's axis of rotation meets its surface. It is called the True North Pole to distinguish from the North magnetic pole, Magnetic North Pole. The North Pole is by definition the northernmost point on the Earth, lying antipode (geography), antipodally to the South Pole. It defines geodetic latitude 90° North, as well as the direction of true north. At the North Pole all directions point south; all lines of longitude converge there, so its longitude can be defined as any degree value. No time zone has been assigned to the North Pole, so any time can be used as the local time. Along tight latitude circles, counterclockwise is east and clockwise is west. The North Pole is at the center of the Northern Hemisphere. The nearest land is usually said to be Kaffeklubben Island, off the northern coast of Greenland about away, though ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sinusoidal With Tissot's Indicatrices Of Distortion
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the ''sine'' and ''cosine'' component ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |