|
Superfactorial
In mathematics, and more specifically number theory, the superfactorial of a positive integer n is the product of the first n factorials. They are a special case of the Jordan–Pólya numbers, which are products of arbitrary collections of factorials. Definition The nth superfactorial \mathit(n) may be defined as: \begin \mathit(n) &= 1!\cdot 2!\cdot \cdots n! = \prod_^ i! = n!\cdot\mathit(n-1)\\ &= 1^n \cdot 2^ \cdot \cdots n = \prod_^ i^.\\ \end Following the usual convention for the empty product, the superfactorial of 0 is 1. The integer sequence of superfactorials, beginning with \mathit(0)=1, is: Properties Just as the factorials can be continuously interpolated by the gamma function, the superfactorials can be continuously interpolated by the Barnes G-function. According to an analogue of Wilson's theorem on the behavior of factorials modulo prime numbers, when p is an odd prime number \mathit(p-1)\equiv(p-1)!!\pmod, where the !! is the notation for the double factor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book '' Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential function an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
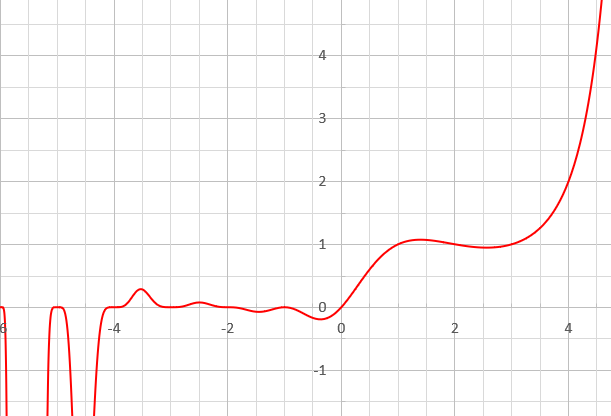
Barnes G-function
In mathematics, the Barnes G-function ''G''(''z'') is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function. Formally, the Barnes ''G''-function is defined in the following Weierstrass product form: : G(1+z)=(2\pi)^ \exp\left(- \frac \right) \, \prod_^\infty \left\ where \, \gamma is the Euler–Mascheroni constant, exp(''x'') = ''e''''x'' is the exponential function, and Π denotes multiplication (capital pi notation). As an entire function, ''G'' is of order two, and of infinite type. This can be deduced from the asymptotic expansion given below. Functional equation and integer arguments The Barnes ''G''-function satisfies the functional equation : G(z+1)=\Gamma(z)\, G(z) with normalisation ''G''(1) = 1. Note the similarity between the functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan–Pólya Number
In mathematics, the Jordan–Pólya numbers are the numbers that can be obtained by multiplying together one or more factorials, not required to be distinct from each other. For instance, 480 is a Jordan–Pólya number because Every tree has a number of symmetries that is a Jordan–Pólya number, and every Jordan–Pólya number arises in this way as the order of an automorphism group of a tree. These numbers are named after Camille Jordan and George Pólya, who both wrote about them in the context of symmetries of trees. These numbers grow more quickly than polynomials but more slowly than exponentials. As well as in the symmetries of trees, they arise as the numbers of transitive orientations of comparability graphs and in the problem of finding factorials that can be represented as products of smaller factorials. Sequence and growth rate The sequence of Jordan–Pólya numbers begins: They form the smallest multiplicatively closed set containing all of the factorials. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empty Product
In mathematics, an empty product, or nullary product or vacuous product, is the result of multiplying no factors. It is by convention equal to the multiplicative identity (assuming there is an identity for the multiplication operation in question), just as the empty sum—the result of adding no numbers—is by convention zero, or the additive identity. When numbers are implied, the empty product becomes one. The term ''empty product'' is most often used in the above sense when discussing arithmetic operations. However, the term is sometimes employed when discussing set-theoretic intersections, categorical products, and products in computer programming; these are discussed below. Nullary arithmetic product Definition Let ''a''1, ''a''2, ''a''3, ... be a sequence of numbers, and let :P_m = \prod_^m a_i = a_1 \cdots a_m be the product of the first ''m'' elements of the sequence. Then :P_m = P_ a_m for all ''m'' = 1, 2, ... provided that we use the convention P_0 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequence
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description. The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, even though we do not have a formula for the ''n''th perfect number. Examples Integer sequences that have their own name include: *Abundant numbers *Baum–Sweet sequence *Bell numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M \ (z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilson's Theorem
In algebra and number theory, Wilson's theorem states that a natural number ''n'' > 1 is a prime number if and only if the product of all the positive integers less than ''n'' is one less than a multiple of ''n''. That is (using the notations of modular arithmetic), the factorial (n - 1)! = 1 \times 2 \times 3 \times \cdots \times (n - 1) satisfies :(n-1)!\ \equiv\; -1 \pmod n exactly when ''n'' is a prime number. In other words, any number ''n'' is a prime number if, and only if, (''n'' − 1)! + 1 is divisible by ''n''. History This theorem was stated by Ibn al-Haytham (c. 1000 AD), and, in the 18th century, by John Wilson. Edward Waring announced the theorem in 1770, although neither he nor his student Wilson could prove it. Lagrange gave the first proof in 1771. There is evidence that Leibniz was also aware of the result a century earlier, but he never published it. Example For each of the values of ''n'' from 2 to 30, the following table shows the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Factorial
In mathematics, the double factorial or semifactorial of a number , denoted by , is the product of all the integers from 1 up to that have the same parity (odd or even) as . That is, :n!! = \prod_^ (n-2k) = n (n-2) (n-4) \cdots. For even , the double factorial is :n!! = \prod_^\frac (2k) = n(n-2)(n-4)\cdots 4\cdot 2 \,, and for odd it is :n!! = \prod_^\frac (2k-1) = n(n-2)(n-4)\cdots 3\cdot 1 \,. For example, . The zero double factorial as an empty product. The sequence of double factorials for even = starts as : 1, 2, 8, 48, 384, 3840, 46080, 645120,... The sequence of double factorials for odd = starts as : 1, 3, 15, 105, 945, 10395, 135135,... The term odd factorial is sometimes used for the double factorial of an odd number. History and usage In a 1902 paper, the physicist Arthur Schuster wrote: states that the double factorial was originally introduced in order to simplify the expression of certain trigonometric integrals that arise in the derivation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being Cube (algebra), cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an intege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Quarterly Journal Of Pure And Applied Mathematics
''The Quarterly Journal of Pure and Applied Mathematics'' was a mathematics journal that first appeared as such in 1855, but as the continuation of ''The Cambridge Mathematical Journal'' that had been launched in 1836 and had run in four volumes before changing its title to ''The Cambridge and Dublin Mathematical Journal'' for a further nine volumes (these latter volumes carried dual numbering). Papers in the first issue, which carried a preface dated April, 1855, and promised further issues on a quarterly schedule in June, September, December and March, have dates going back to November, 1854; the first volume carried a further preface dated January, 1857. From the outset, keeping the journal up and running was to prove a challenging task. It was edited under the new title by James Joseph Sylvester and Norman Macleod Ferrers, assisted by George G. Stokes and Arthur Cayley, with Charles Hermite as corresponding editor in Paris, an arrangement that remained stable for the first fif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PRIMUS (journal)
''PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies'' is a peer-reviewed academic journal covering the teaching of undergraduate mathematics, established in 1991. The journal has been published by Taylor & Francis since March 2007. It is abstracted and indexed in Cambridge Scientific Abstracts, MathEduc, PsycINFO, and ''Zentralblatt MATH''. PRIMUS is an affiliated journal of the Mathematical Association of America, so all MAA members have access to PRIMUS. Editorial Team PRIMUS was started by founding editor-in-chief Brian Winkel in 1991 to address the lack of venues for tertiary mathematics educators to share their pedagogical work. In 2011, Jo Ellis-Monaghan Joanna Anthony Ellis-Monaghan is an American mathematician and mathematics educator whose research interests include graph polynomials and topological graph theory. She is a professor of mathematics at the Korteweg-de Vries Institute for Mathema ... became the second editor-in-chief, with Ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
