|
Sub-multiplicative Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
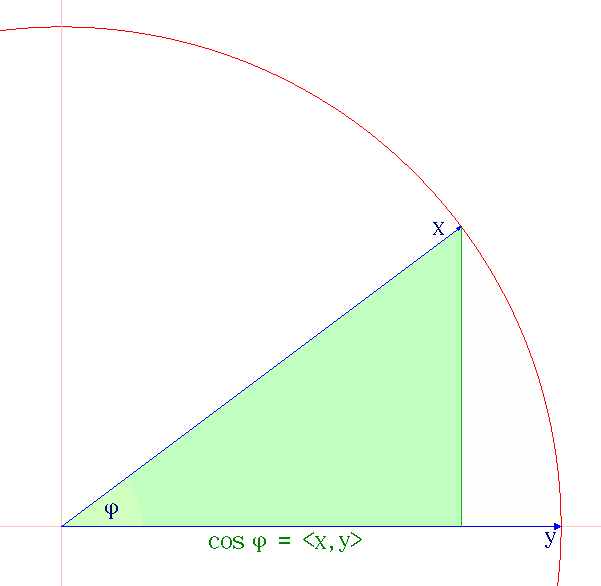
Euclidean Norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the '' Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Coding
Neural coding (or Neural representation) is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the individual or ensemble neuronal responses and the relationship among the electrical activity of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by networks of neurons, it is thought that neurons can encode both digital and analog information. Overview Neurons are remarkable among the cells of the body in their ability to propagate signals rapidly over large distances. They do this by generating characteristic electrical pulses called action potentials: voltage spikes that can travel down axons. Sensory neurons change their activities by firing sequences of action potentials in various temporal patterns, with the presence of external sensory stimuli, such as light, sound, taste, smell and touch. It is known that information about the stimulus is encoded in this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Data Analysis
Robust statistics are statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normal. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but which are not unduly affected by outliers or other small departures from model assumptions. In statistics, classical estimation methods rely heavily on assumptions which are often no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although note that in quantum mechanics, A^\ast typically means the complex conjugate only, and not the conjugate transpose. Alternative characterizations Hermit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by . Definition Matrices Let be the eigenvalues of a matrix . The spectral radius of is defined as :\rho(A) = \max \left \. The spectral radius can be thought of as an infimum of all norms of a matrix. Indeed, on the one hand, \rho(A) \leqslant \, A\, for every natural matrix norm \, \cdot\, ; and on the other hand, Gelfand's formula states that \rho(A) = \lim_ \, A^k\, ^ . Both of these results are shown below. However, the spectral radius does not necessarily satisfy \, A\mathbf\, \leqslant \rho(A) \, \mathbf\, for arbitrary vectors \mathbf \in \mathbb^n . To see why, let r > 1 be arbitrary and consider the matrix : C_r = \begin 0 & r^ \\ r & 0 \end . The characteristic polynomial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistent And Compatible Norms
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if it has a model, i.e., there exists an interpretation under which all formulas in the theory are true. This is the sense used in traditional Aristotelian logic, although in contemporary mathematical logic the term ''satisfiable'' is used instead. The syntactic definition states a theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences of T. Let A be a set of closed sentences (informally "axioms") and \langle A\rangle the set of closed sentences provable from A under some (specified, possibly implicitly) formal deductive system. The set of axioms A is consistent when \varphi, \lnot \varphi \in \langle A \rangle for no formula \varphi. If there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-negative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frobenius Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any \ m \times n\ matrix. It is related to the polar decomposition. Specifically, the singular value decomposition of an \ m \times n\ complex matrix is a factorization of the form \ \mathbf = \mathbf\ , where is an \ m \times m\ complex unitary matrix, \ \mathbf\ is an \ m \times n\ rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \ \mathbf\ is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrices; in such contexts, the SVD is often denoted \ \mathbf^\mathsf\ . The diagonal entries \ \sigma_i = \Sigma_\ of \ \mathbf\ are uniquely determined by and are known as the singular values of . The n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Transpose
In mathematics, the conjugate transpose, also known as the Hermitian transpose, of an m \times n complex matrix \boldsymbol is an n \times m matrix obtained by transposing \boldsymbol and applying complex conjugate on each entry (the complex conjugate of a+ib being a-ib, for real numbers a and b). It is often denoted as \boldsymbol^\mathrm or \boldsymbol^* or \boldsymbol'. H. W. Turnbull, A. C. Aitken, "An Introduction to the Theory of Canonical Matrices," 1932. For real matrices, the conjugate transpose is just the transpose, \boldsymbol^\mathrm = \boldsymbol^\mathsf. Definition The conjugate transpose of an m \times n matrix \boldsymbol is formally defined by where the subscript ij denotes the (i,j)-th entry, for 1 \le i \le n and 1 \le j \le m, and the overbar denotes a scalar complex conjugate. This definition can also be written as :\boldsymbol^\mathrm = \left(\overline\right)^\mathsf = \overline where \boldsymbol^\mathsf denotes the transpose and \overline denotes the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |