Cauchy–Schwarz inequality on:
[Wikipedia]
[Google]
[Amazon]
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the
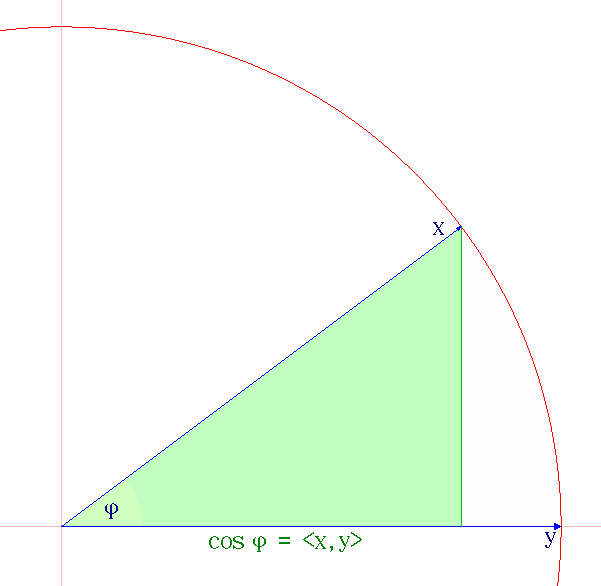 The real vector space denotes the 2-dimensional plane. It is also the 2-dimensional
The real vector space denotes the 2-dimensional plane. It is also the 2-dimensional
Earliest Uses: The entry on the Cauchy–Schwarz inequality has some historical information.
Tutorial and Interactive program. {{DEFAULTSORT:Cauchy-Schwarz inequality Augustin-Louis Cauchy Inequalities (mathematics) Linear algebra Operator theory Articles containing proofs Mathematical analysis Probabilistic inequalities
absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics.
Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
s (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version.
Statement of the inequality
The Cauchy–Schwarz inequality states that for all vectors and of an inner product space where is the inner product. Examples of inner products include the real and complexdot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
; see the examples in inner product. Every inner product gives rise to a Euclidean norm, called the or , where the norm of a vector is denoted and defined by
where is always a non-negative real number (even if the inner product is complex-valued).
By taking the square root of both sides of the above inequality, the Cauchy–Schwarz inequality can be written in its more familiar form in terms of the norm:
Moreover, the two sides are equal if and only if and are linearly dependent.
Special cases
Sedrakyan's lemma – positive real numbers
Sedrakyan's inequality, also known as Bergström's inequality, Engel's form, Titu's lemma (or the T2 lemma), states that for real numbers and positive real numbers : or, using summation notation, It is a direct consequence of the Cauchy–Schwarz inequality, obtained by using thedot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
on upon substituting and . This form is especially helpful when the inequality involves fractions where the numerator is a perfect square.
- The plane
 The real vector space denotes the 2-dimensional plane. It is also the 2-dimensional
The real vector space denotes the 2-dimensional plane. It is also the 2-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
where the inner product is the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
.
If and then the Cauchy–Schwarz inequality becomes:
where is the angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
between and .
The form above is perhaps the easiest in which to understand the inequality, since the square of the cosine can be at most 1, which occurs when the vectors are in the same or opposite directions. It can also be restated in terms of the vector coordinates , , , and as
where equality holds if and only if the vector is in the same or opposite direction as the vector , or if one of them is the zero vector.
: ''n''-dimensional Euclidean space
InEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
with the standard inner product, which is the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
, the Cauchy–Schwarz inequality becomes:
The Cauchy–Schwarz inequality can be proved using only elementary algebra in this case by observing that the difference of the right and the left hand side is
or by considering the following quadratic polynomial in
Since the latter polynomial is nonnegative, it has at most one real root, hence its discriminant is less than or equal to zero. That is,
: ''n''-dimensional complex space
If with and (where and ) and if the inner product on the vector space is the canonical complex inner product (defined by where the bar notation is used for complex conjugation), then the inequality may be restated more explicitly as follows: That is,For the inner product space of square-integrable complex-valued functions, the following inequality holds. The Hölder inequality is a generalization of this.
Applications
Analysis
In any inner product space, the triangle inequality is a consequence of the Cauchy–Schwarz inequality, as is now shown: Taking square roots gives the triangle inequality: The Cauchy–Schwarz inequality is used to prove that the inner product is a continuous function with respect to thetopology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
induced by the inner product itself.
Geometry
The Cauchy–Schwarz inequality allows one to extend the notion of "angle between two vectors" to any real inner-product space by defining: The Cauchy–Schwarz inequality proves that this definition is sensible, by showing that the right-hand side lies in the interval and justifies the notion that (real) Hilbert spaces are simply generalizations of theEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. It can also be used to define an angle in complex inner-product spaces, by taking the absolute value or the real part of the right-hand side, as is done when extracting a metric from quantum fidelity.
Probability theory
Let and berandom variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s. Then the covariance inequality is given by:
After defining an inner product on the set of random variables using the expectation of their product,
the Cauchy–Schwarz inequality becomes
To prove the covariance inequality using the Cauchy–Schwarz inequality, let and then
where denotes variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
and denotes covariance.
Proofs
There are many different proofs of the Cauchy–Schwarz inequality other than those given below. When consulting other sources, there are often two sources of confusion. First, some authors define to be linear in the second argument rather than the first. Second, some proofs are only valid when the field is and not This section gives two proofs of the following theorem: In both of the proofs given below, the proof in the trivial case where at least one of the vectors is zero (or equivalently, in the case where ) is the same. It is presented immediately below only once to reduce repetition. It also includes the easy part of the proof of the Equality Characterization given above; that is, it proves that if and are linearly dependent then By definition, and are linearly dependent if and only if one is a scalar multiple of the other. If where is some scalar then which shows that equality holds in the . The case where for some scalar follows from the previous case: In particular, if at least one of and is the zero vector then and are necessarily linearly dependent (for example, if then where ), so the above computation shows that the Cauchy–Schwarz inequality holds in this case. Consequently, the Cauchy–Schwarz inequality only needs to be proven only for non-zero vectors and also only the non-trivial direction of the Equality Characterization must be shown.Proof via the Pythagorean theorem
The special case of was proven above so it is henceforth assumed that Let It follows from the linearity of the inner product in its first argument that: Therefore, is a vector orthogonal to the vector (Indeed, is the projection of onto the plane orthogonal to ) We can thus apply the Pythagorean theorem to which gives The Cauchy–Schwarz inequality follows by multiplying by and then taking the square root. Moreover, if the relation in the above expression is actually an equality, then and hence the definition of then establishes a relation of linear dependence between and The converse was proved at the beginning of this section, so the proof is complete.Proof by analyzing a quadratic
Consider an arbitrary pair of vectors . Define the function defined by , where is a complex number satisfying and . Such an exists since if then can be taken to be 1. Since the inner product is positive-definite, only takes non-negative real values. On the other hand, can be expanded using the bilinearity of the inner product: Thus, is a polynomial of degree (unless which is a case that was checked earlier). Since the sign of does not change, the discriminant of this polynomial must be non-positive: The conclusion follows. For the equality case, notice that happens if and only if If then and henceGeneralizations
Various generalizations of the Cauchy–Schwarz inequality exist.Hölder's inequality
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality (mathematics), inequality between Lebesgue integration, integrals and an indispensable tool for the study of Lp space, spaces.
The numbers an ...
generalizes it to norms. More generally, it can be interpreted as a special case of the definition of the norm of a linear operator on a Banach space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and ...
(Namely, when the space is a Hilbert space). Further generalizations are in the context of operator theory, e.g. for operator-convex functions and operator algebras, where the domain and/or range are replaced by a C*-algebra or W*-algebra.
An inner product can be used to define a positive linear functional. For example, given a Hilbert space being a finite measure, the standard inner product gives rise to a positive functional by Conversely, every positive linear functional on can be used to define an inner product where is the pointwise complex conjugate of In this language, the Cauchy–Schwarz inequality becomes
which extends verbatim to positive functionals on C*-algebras:
The next two theorems are further examples in operator algebra.
This extends the fact when is a linear functional. The case when is self-adjoint, that is, is sometimes known as Kadison's inequality.
Another generalization is a refinement obtained by interpolating between both sides of the Cauchy–Schwarz inequality:
This theorem can be deduced from Hölder's inequality
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality (mathematics), inequality between Lebesgue integration, integrals and an indispensable tool for the study of Lp space, spaces.
The numbers an ...
. There are also non-commutative versions for operators and tensor products of matrices.
Several matrix versions of the Cauchy–Schwarz inequality and Kantorovich inequality are applied to linear regression models.
See also
* * * * * * *Notes
Citations
References
* * * * * * * . * * . * * *External links
Earliest Uses: The entry on the Cauchy–Schwarz inequality has some historical information.
Tutorial and Interactive program. {{DEFAULTSORT:Cauchy-Schwarz inequality Augustin-Louis Cauchy Inequalities (mathematics) Linear algebra Operator theory Articles containing proofs Mathematical analysis Probabilistic inequalities