|
Spatial Network
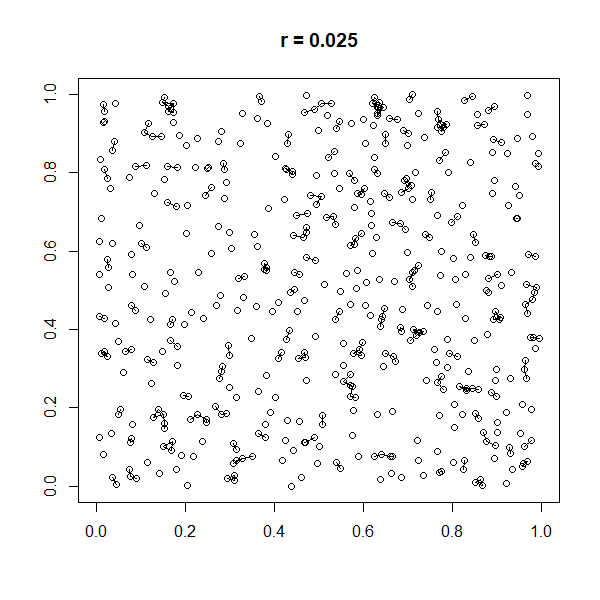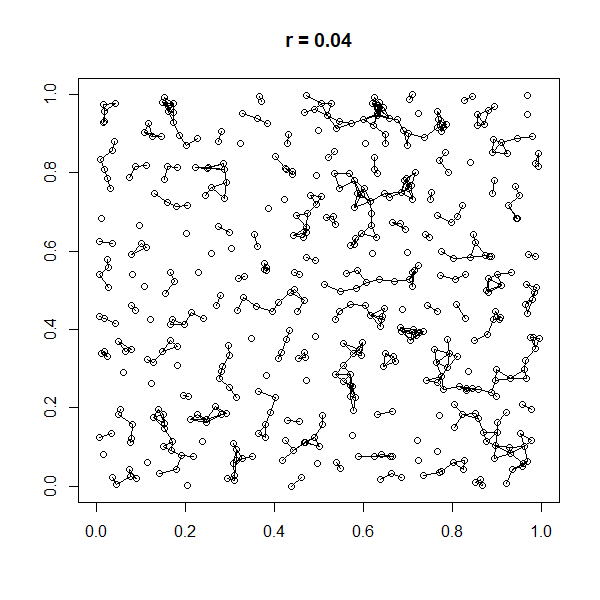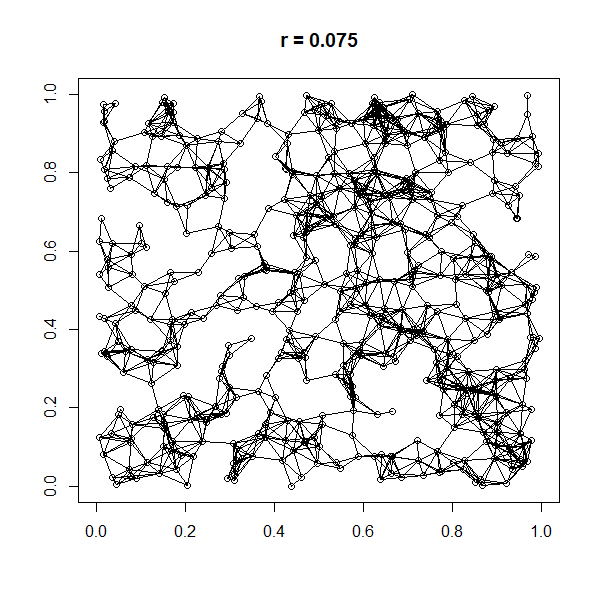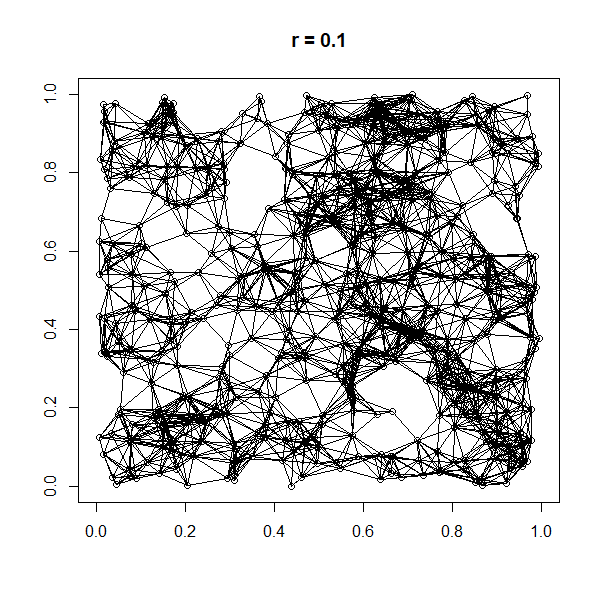
A spatial network (sometimes also Geometric graph theory, geometric graph) is a Graph (discrete mathematics), graph in which the Vertex (graph theory), vertices or Edge (graph theory), edges are ''spatial elements'' associated with Geometry, geometric objects, i.e., the nodes are located in a space equipped with a certain Metric (mathematics), metric.M. Barthelemy, "Morphogenesis of Spatial Networks", Springer (2018). The simplest mathematical realization of spatial network is a Lattice graph, lattice or a random geometric graph (see figure in the right), where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transport network, Transportation and mobility networks, Internet, cellular network, mobile phone networks, electrical grid, power grids, social network, social and contact networks and neural network, biological neural networks are all examples where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Geometric Graph
In graph theory, a random geometric graph (RGG) is the mathematically simplest spatial network, namely an undirected graph constructed by randomly placing ''N'' nodes in some metric space (according to a specified probability distribution) and connecting two nodes by a link if and only if their distance is in a given range, e.g. smaller than a certain neighborhood radius, ''r''. Random geometric graphs resemble real human social networks in a number of ways. For instance, they spontaneously demonstrate community structure - clusters of nodes with high modularity. Other random graph generation algorithms, such as those generated using the Erdős–Rényi model or Barabási–Albert (BA) model do not create this type of structure. Additionally, random geometric graphs display degree assortativity according to their spatial dimension: "popular" nodes (those with many links) are particularly likely to be linked to other popular nodes. A real-world application of RGGs is the modeli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transportation Network (graph Theory)
In graph theory, a flow network (also known as a transportation network) is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A network can be used to model traffic in a computer network, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes. Definition A network is a graph , where is a set of vertices and is a set of 's edges – a subset of – together with a non-negative function , called the capacity function. Without loss of generality, we may assume that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Line
{{disambiguation ...
Axial may refer to: * one of the anatomical directions describing relationships in an animal body * In geometry: :* a geometric term of location :* an axis of rotation * In chemistry, referring to an axial bond * a type of modal frame, in music * axial-flow, a type of fan * the Axial age in China, India, etc. * Axial Seamount and submarine volcano off Oregon, USA * Axial, Colorado, a ghost town See also *Axiality (other) *Axis (other) An axis (plural ''axes'') is an imaginary line around which an object rotates or is symmetrical. Axis may also refer to: Mathematics * Axis of rotation: see rotation around a fixed axis *Axis (mathematics), a designator for a Cartesian-coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Syntax
The term space syntax encompasses a set of theories and techniques for the analysis of spatial configurations. It was conceived by Bill Hillier, Julienne Hanson, and colleagues at The Bartlett, University College London in the late 1970s to early 1980s to develop insights into the mutually constructive relation between society and space. As space syntax has evolved, certain measures have been found to correlate with human spatial behavior, and space syntax has thus come to be used to forecast likely effects of architectural and urban space on users. Thesis The general idea is that spaces can be broken down into components, analyzed as networks of choices, then represented as maps and graphs that describe the relative connectivity and integration of those spaces. It rests on three basic conceptions of space: * an isovist (popularised by Michael Benedikt at University of Texas), or viewshed or visibility polygon, the field of view from any particular point * axial space (idea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percolation Theory
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory and percolation. Introduction A representative question (and the source of the name) is as follows. Assume that some liquid is poured on top of some porous material. Will the liquid be able to make its way from hole to hole and reach the bottom? This physical question is modelled mathematically as a three-dimensional network of vertices, usually called "sites", in which the edge or "bonds" between each two neighbors may be open (allowing the liquid through) with probability , or closed with probability , and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erdős–Rényi Model
In the mathematical field of graph theory, the Erdős–Rényi model is either of two closely related models for generating random graphs or the evolution of a random network. They are named after Hungarian mathematicians Paul Erdős and Alfréd Rényi, who first introduced one of the models in 1959, while Edgar Gilbert introduced the other model contemporaneously and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely; in the model introduced by Gilbert, also called the Erdős–Rényi–Gilbert model, each edge has a fixed probability of being present or absent, independently of the other edges. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs. Definition There are two closely related variants of the Erdős–R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Line Process
Poisson may refer to: People *Siméon Denis Poisson, French mathematician Places *Poissons, a commune of Haute-Marne, France *Poisson, Saône-et-Loire, a commune of Saône-et-Loire, France Other uses *Poisson (surname), a French surname *Poisson (crater), a lunar crater named after Siméon Denis Poisson *The French word for fish See also *Adolphe-Poisson Bay, a body of water located to the southwest of Gouin Reservoir, in La Tuque, Mauricie, Quebec *Poisson distribution, a discrete probability distribution named after Siméon Denis Poisson *Poisson's equation, a partial differential equation named after Siméon Denis Poisson *List of things named after Siméon Denis Poisson These are things named after Siméon Denis Poisson (1781 – 1840), a French mathematician. Physics * ''Poisson’s Equations'' (thermodynamics) * ''Poisson’s Equation'' (rotational motion) * Schrödinger–Poisson equation * Vlasov–Poisson equ ... * Poison (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Poisson Process
In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy,G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of statistical planning and inference'', 50(3):311–326, 1996. biology,H. G. Othmer, S. R. Dunbar, and W. Alt. Models of dispersal in biological systems. ''Journal of mathematical biology'', 26(3):263–298, 1988. ecology,H. Thompson. Spatial point proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Neighborhood Graph
In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points p and q by an edge whenever there does not exist a third point r that is closer to both p and q than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.. Algorithms showed how to construct the relative neighborhood graph of n points in the plane efficiently in O(n\log n) time. It can be computed in O(n) expected time, for random set of points distributed uniformly in the unit square. The relative neighborhood graph can be computed in linear time from the Delaunay triangulation of the point set.. Generalizations Because it is defined only in terms of the distances between points, the relative neighborhood graph can be defined for point sets in any and for non-Euclidean metrics. Comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steiner Tree
In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals (but may include additional vertices). Further well-known variants are the ''Euclidean Steiner tree problem'' and the '' rectilinear minimum Steiner tree problem''. The Steiner tree problem in graphs can be seen as a generalization of two other famous combinatorial optimization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Spanning Tree
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components. There are many use cases for minimum spanning trees. One example is a telecommunications company trying to lay cable in a new neighborhood. If it is constrained to bury the cable only along certain paths (e.g. roads), then there would be a graph containing the points (e.g. houses) connected by those paths. Some of the paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (graph Theory)
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is denoted \deg(v) or \deg v. The maximum degree of a graph G, denoted by \Delta(G), and the minimum degree of a graph, denoted by \delta(G), are the maximum and minimum of its vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, every vertex has the same degree, and so we can speak of ''the'' degree of the graph. A complete graph (denoted K_n, where n is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum possible degree, n-1. In a signed graph, the number of positive edges connected to the vertex v is called positive deg(v) and the number of connected negative edges is entitled negative deg(v). Handshaking lemma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Degree (graph Theory)")