Random Geometric Graph

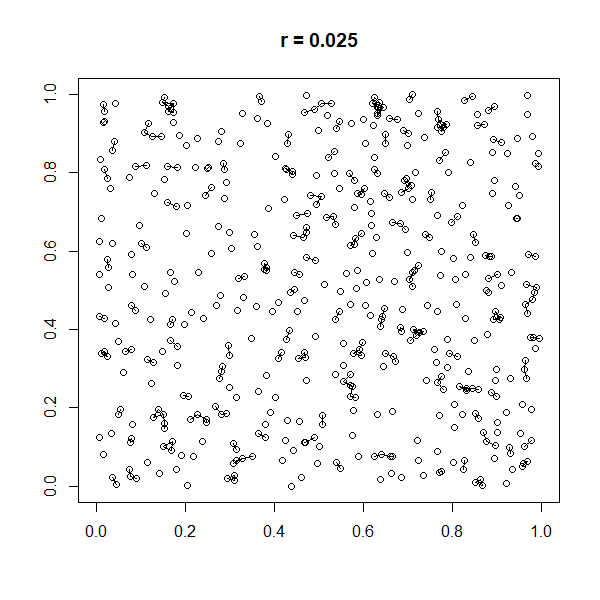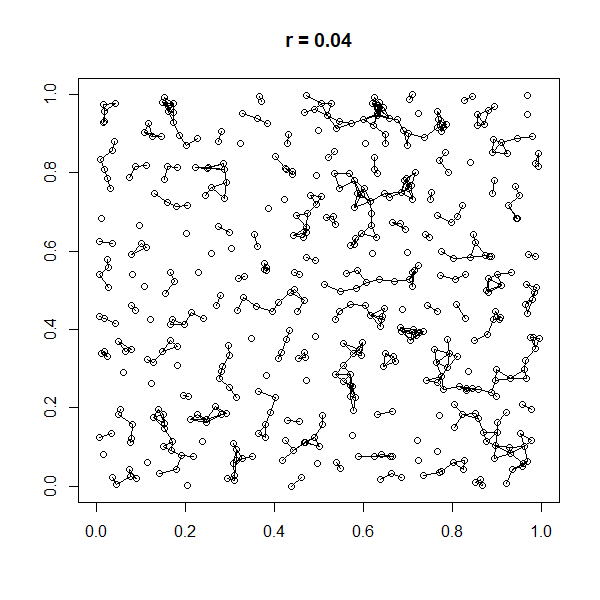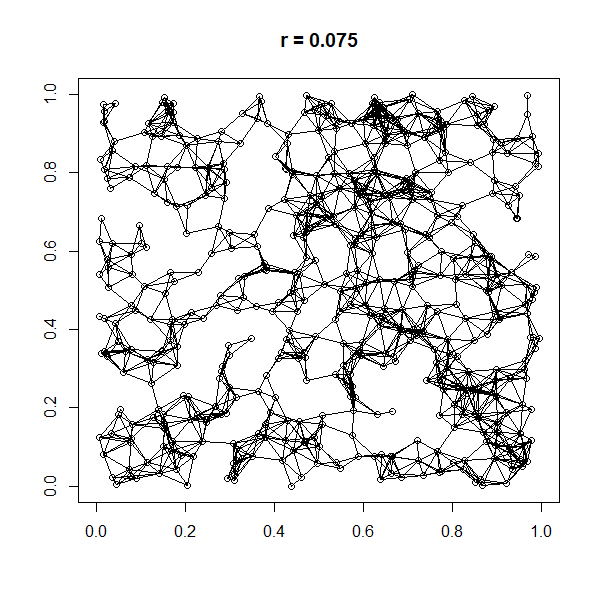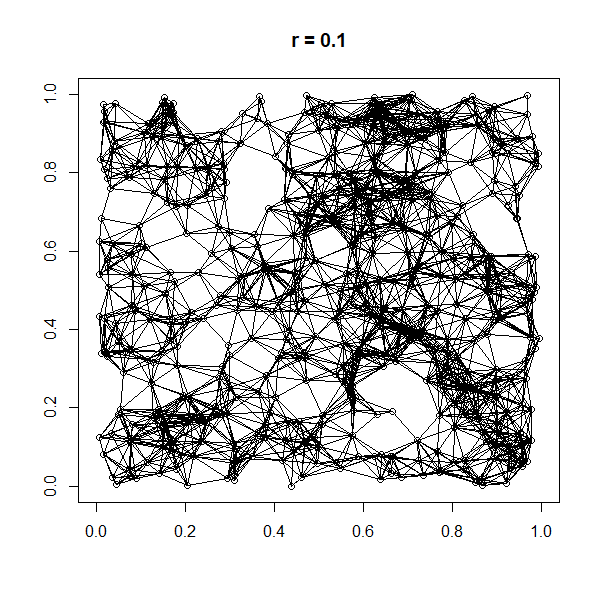
In graph theory, a random geometric graph (RGG) is the mathematically simplest spatial network, namely an undirected graph constructed by randomly placing ''N'' nodes in some metric space (according to a specified probability distribution) and connecting two nodes by a link if and only if their distance is in a given range, e.g. smaller than a certain neighborhood radius, ''r''.

Random geometric graphs resemble real human social networks in a number of ways. For instance, they spontaneously demonstrate community structure - clusters of nodes with high modularity. Other random graph generation algorithms, such as those generated using the Erdős–Rényi model or Barabási–Albert (BA) model do not create this type of structure. Additionally, random geometric graphs display degree assortativity according to their spatial dimension: "popular" nodes (those with many links) are particularly likely to be linked to other popular nodes.

A real-world application of RGGs is the modeling of ad hoc networks. Furthermore they are used to perform benchmarks for graph algorithms.

Definition

In the following, let  denote an undirected Graph with a set of vertices and a set of edges . The set sizes are denoted by and . Additionally, if not noted otherwise, the metric space with the euclidean distance is considered, i.e. for any points x, y \in , x - y, , _2 = \sqrt.

A random geometric graph (RGG) is an undirected geometric graph with nodes randomly sampled from the uniform distribution of the underlying space . Two vertices are connected if, and only if, their distance is less than a previously specified parameter , excluding any Loop (graph theory), loops. Thus, the parameters and fully characterize a RGG.

Algorithms

Naive algorithm

The naive approach is to calculate the distance of every vertex to every other vertex. As there are $\frac$possible connections that are checked, the time complexity of the naive algorithm is $\Theta(n^2)$. The samples are generated by using a Random number generation, random number generator (RNG) on $[0, 1)^d$. Practically, one can implement this using d random number generators on $[0, 1)$, one RNG for every dimension.

Pseudocode

''V'' := generateSamples(''n'') ''// Generates n samples in the unit cube.''
for each ''p'' ∈ ''V'' do
for each ''q'' ∈ ''V''\ do
if distance(''p'', ''q'') ≤ ''r'' then
addConnection(''p'', ''q'') ''// Add the edge (p, q) to the edge data structure.''
end if
end for
end for

As this algorithm is not scalable (every vertex needs information of every other vertex), Holtgrewe et al. and Funke et al. have introduced new algorithms for this problem.

Distributed algorithms

Holtgrewe et al.

This algorithm, which was proposed by Holtgrewe et al., was the first distributed RGG generator algorithm for dimension 2. It partitions the unit square into equal sized cells with side length of at least $r$. For a given number $P = p^2$of processors, each processor is assigned $\times$cells, where $k = \left \lfloor \right \rfloor.$For simplicity, $P$ is assumed to be a square number, but this can be generalized to any number of processors. Each processor then generates $\frac$vertices, which are then distributed to their respective owners. Then the vertices are sorted by the cell number they fall into, for example with Quicksort. Next, each processor then sends their adjacent processors the information about the vertices in the border cells, such that each processing unit can calculate the edges in their partition independent of the other units. The expected running time is $O(\frac\log)$. An upper bound for the communication cost of this algorithm is given by $T_(n/P, P) + T_(1, P) + T_(n/(k\cdot) + 2)$, where $T_(l, c)$denotes the time for an all-to-all communication with messages of length bits to communication partners. $T_(l)$is the time taken for a point-to-point communication for a message of length bits.

Since this algorithm is not communication free, Funke et al. proposed a scalable distributed RGG generator for higher dimensions, which works without any communication between the processing units.

Funke et al.

The approach used in this algorithm is similar to the approach in Holtgrewe: Partition the unit cube into equal sized chunks with side length of at least . So in = 2 this will be squares, in = 3 this will be cubes. As there can only fit at most $$ chunks per dimension, the number of chunks is capped at $^d$. As before, each processor is assigned $^d \over P$chunks, for which it generates the vertices. To achieve a communication free process, each processor then generates the same vertices in the adjacent chunks by exploiting pseudorandomization of seeded hash functions. This way, each processor calculates the same vertices and there is no need for exchanging vertex information.

For dimension 3, Funke et al. showed that the expected running time is $O(\frac + \log)$, without any cost for communication between processing units.

Properties

Isolated vertices and connectivity

The probability that a single vertex is isolated in a RGG is $(1- \pi r^2)^$. Let $X$ be the random variable counting how many vertices are isolated. Then the expected value of $X$is $E(X) = n(1- \pi r^2)^ = ne^-O(r^4n)$. The term $\mu = ne^$provides information about the connectivity of the RGG. For $\mu \longrightarrow 0$, the RGG is asymptotically almost surely connected. For $\mu \longrightarrow \infin$, the RGG is asymptotically almost surely disconnected. And for $\mu = \Theta(1)$, the RGG has a giant component that covers more than $\frac$vertices and $X$ is Poisson distributed with parameter $\mu$. It follows that if $\mu = \Theta(1)$, the probability that the RGG is connected is P =0\sim e^and the probability that the RGG is not connected is P >0\sim 1-e^.

For any $l_p$-Norm ( $1 \leq p \leq \infin$) and for any number of dimensions $d>2$, a RGG possesses a sharp threshold of connectivity at $r \sim()^$with constant $\alpha_$. In the special case of a two-dimensional space and the euclidean norm ($d=2$ and $p=2$) this yields $r \sim \sqrt$.

Hamiltonicity

It has been shown, that in the two-dimensional case, the threshold $r \sim \sqrt$also provides information about the existence of a Hamiltonian cycle (Hamiltonian Path). For any $\epsilon>0$, if $r \sim \sqrt$, then the RGG has asymptotically almost surely no Hamiltonian cycle and if $r \sim \sqrt$for any $\epsilon>0$, then the RGG has asymptotically almost surely a Hamiltonian cycle.

Clustering coefficient

The clustering coefficient of RGGs only depends on the dimension of the underlying space . The clustering coefficient is

$C_d = 1-H_d(1)$for even $d$ and $C_d = -H_d()$for odd $d$where$H_d(x) = \sum_^ ()^$For large $d$, this simplifies to $C_d \sim 3 \sqrt ()^$.

Generalized random geometric graphs

In 1988 Waxman generalised the standard RGG by introducing a probabilistic connection function as opposed to the deterministic one suggested by Gilbert. The example introduced by Waxman was a stretched exponential where two nodes $i$ and $j$ connect with probability given by $H_=\beta e^$where $r_$ is the euclidean separation and $\beta$, $r_0$are parameters determined by the system. This type of RGG with probabilistic connection function is often referred to a soft random geometric Graph, which now has two sources of randomness; the location of nodes (vertices) and the formation of links (edges). This connection function has been generalized further in the literature $H_=\beta e^$which is often used to study wireless networks without interference. The parameter $\eta$ represents how the signal decays with distance, when $\eta =2$ is free space, $\eta >2$ models a more cluttered environment like a town (= 6 models cities like New York) whilst $\eta <2$ models highly reflective environments. We notice that for $\eta =1$ is the Waxman model, whilst as $\eta \to \infin$ and $\beta =1$ we have the standard RGG. Intuitively these type of connection functions model how the probability of a link being made decays with distance.

Overview of some results for Soft RGG

In the high density limit for a network with exponential connection function the number of isolated nodes is Poisson distributed, and the resulting network contains a unique giant component and isolated nodes only. Therefore by ensuring there are no isolated nodes, in the dense regime, the network is a.a.s fully connected; similar to the results shown in for the disk model. Often the properties of these networks such as betweenness centrality and connectivity are studied in the limit as the density $\to \infin$ which often means border effects become negligible. However, in real life where networks are finite, although can still be extremely dense, border effects will impact on full connectivity; in fact showed that for full connectivity, with an exponential connection function, is greatly impacted by boundary effects as nodes near the corner/face of a domain are less likely to connect compared with those in the bulk. As a result full connectivity can be expressed as a sum of the contributions from the bulk and the geometries boundaries. A more general analysis of the connection functions in wireless networks has shown that the probability of full connectivity can be well approximated expressed by a few moments of the connection function and the regions geometry.{{cite journal, last1=Dettmann, first1=C.P, last2=Georgiou, first2=O, date=2016, title=Random geometric graphs with general connection functions, journal=Physical Review E, volume=93, issue=3, pages=032313, arxiv=1411.3617, bibcode=2016PhRvE..93c2313D, doi=10.1103/physreve.93.032313, pmid=27078372, s2cid=124506496

References

Geometric graphs
Random graphs