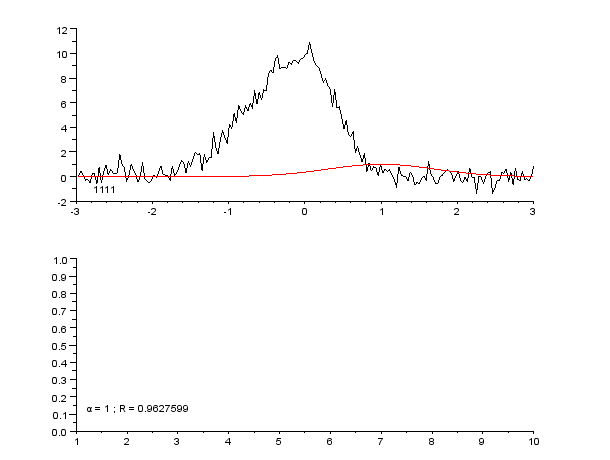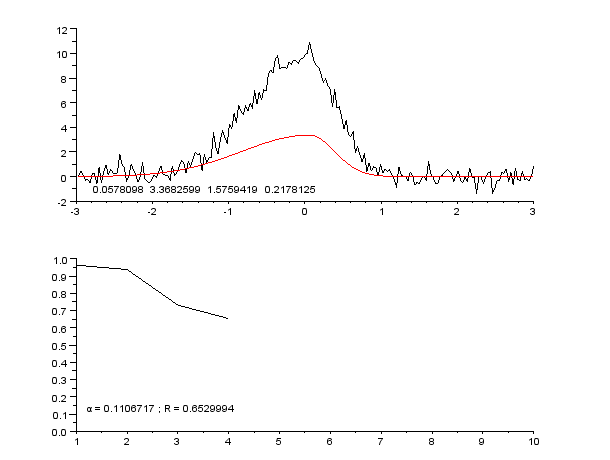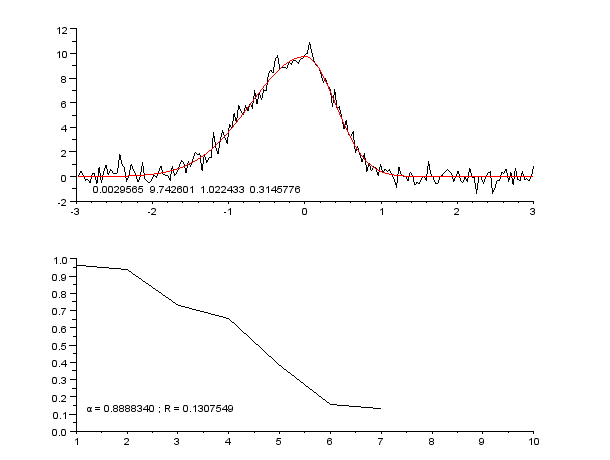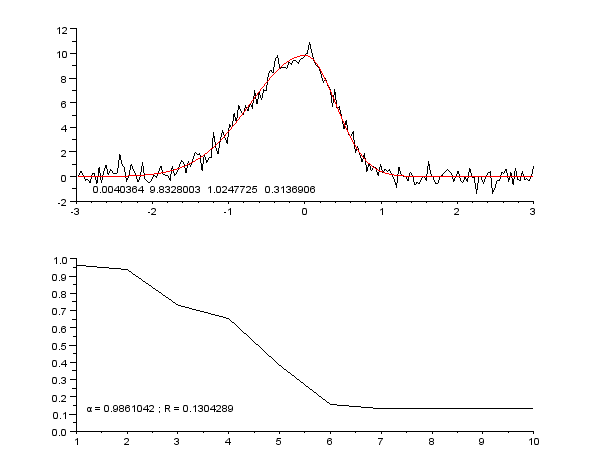
|
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. In smoothing, the data points of a signal are modified so individual points higher than the adjacent points (presumably because of noise) are reduced, and points that are lower than the adjacent points are increased leading to a smoother signal. Smoothing may be used in two important ways that can aid in data analysis (1) by being able to extract more information from the data as long as the assumption of smoothing is reasonable and (2) by being able to provide analyses that are both flexible and robust. Many different algorithms are used in smoothing. Compared to curve fitting Smoothing may be distinguished from the related and partially overlapping concept of curve fitting in the following ways: * curve fitting often involves the use of an explicit functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Additive Smoothing
In statistics, additive smoothing, also called Laplace smoothing or Lidstone smoothing, is a technique used to smooth count data, eliminating issues caused by certain values having 0 occurrences. Given a set of observation counts \mathbf = \langle x_1, x_2, \ldots, x_d \rangle from a d-dimensional multinomial distribution with N trials, a "smoothed" version of the counts gives the estimator : \hat\theta_i = \frac \qquad (i = 1, \ldots, d), where the smoothed count \hat x_i = N \hat\theta_i, and the "pseudocount" ''α'' > 0 is a smoothing parameter, with ''α'' = 0 corresponding to no smoothing (this parameter is explained in below). Additive smoothing is a type of shrinkage estimator, as the resulting estimate will be between the empirical probability ( relative frequency) x_i/N and the uniform probability 1/d. Common choices for ''α'' are 0 (no smoothing), (the Jeffreys prior), or 1 (Laplace's rule of succession), but the parameter may also be set empi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Space
Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision. It is a formal theory for handling image structures at different scales, by representing an image as a one-parameter family of smoothed images, the scale-space representation, parametrized by the size of the smoothing kernel used for suppressing fine-scale structures. The parameter t in this family is referred to as the ''scale parameter'', with the interpretation that image structures of spatial size smaller than about \sqrt have largely been smoothed away in the scale-space level at scale t. The main type of scale space is the ''linear (Gaussian) scale space'', which has wide applicability as well as the attractive property of being possible to derive from a small set of '' scale-space axioms''. The corresponding scale-space framework encompasses a th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moving Average (finance)
In statistics, a moving average (rolling average or running average or moving mean or rolling mean) is a calculation to analyze data points by creating a series of averages of different selections of the full data set. Variations include: simple, cumulative, or weighted forms. Mathematically, a moving average is a type of convolution. Thus in signal processing it is viewed as a low-pass finite impulse response filter. Because the boxcar function outlines its filter coefficients, it is called a boxcar filter. It is sometimes followed by downsampling. Given a series of numbers and a fixed subset size, the first element of the moving average is obtained by taking the average of the initial fixed subset of the number series. Then the subset is modified by "shifting forward"; that is, excluding the first number of the series and including the next value in the series. A moving average is commonly used with time series data to smooth out short-term fluctuations and highlight longe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ripple (filters)
Ripple (specifically ripple voltage) in electronics is the residual periodic variation of the DC voltage within a power supply which has been derived from an alternating current (AC) source. This ripple is due to incomplete suppression of the alternating waveform after rectification. Ripple voltage originates as the output of a rectifier or from generation and commutation of DC power. Ripple (specifically ripple current or surge current) may also refer to the pulsed current consumption of non-linear devices like capacitor-input rectifiers. As well as these time-varying phenomena, there is a frequency domain ripple that arises in some classes of filter and other signal processing networks. In this case the periodic variation is a variation in the insertion loss of the network against increasing frequency. The variation may not be strictly linearly periodic. In this meaning also, ripple is usually to be considered an incidental effect, its existence being a compromise between th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve Fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fitted to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. For linear-algebraic ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution Kernel
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus it is a cross-correlation of g(-x) and f(x), or f(-x) and g(x) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hat Matrix
In statistics, the projection matrix (\mathbf), sometimes also called the influence matrix or hat matrix (\mathbf), maps the vector of response values (dependent variable values) to the vector of fitted values (or predicted values). It describes the influence each response value has on each fitted value. The diagonal elements of the projection matrix are the leverages, which describe the influence each response value has on the fitted value for that same observation. Definition If the vector of response values is denoted by \mathbf and the vector of fitted values by \mathbf, :\mathbf = \mathbf \mathbf. As \mathbf is usually pronounced "y-hat", the projection matrix \mathbf is also named ''hat matrix'' as it "puts a hat on \mathbf". Application for residuals The formula for the vector of residuals \mathbf can also be expressed compactly using the projection matrix: :\mathbf = \mathbf - \mathbf = \mathbf - \mathbf \mathbf = \left( \mathbf - \mathbf \right) \mathbf. where \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roll-off
Roll-off is the steepness of a transfer function with frequency, particularly in electrical network analysis, and most especially in connection with filter circuits in the transition between a passband and a stopband. It is most typically applied to the insertion loss of the network, but can, in principle, be applied to any relevant function of frequency, and any technology, not just electronics. It is usual to measure roll-off as a function of logarithmic frequency; consequently, the units of roll-off are either decibels per decade (dB/decade), where a decade is a tenfold increase in frequency, or decibels per octave (dB/8ve), where an octave is a twofold increase in frequency. The concept of roll-off stems from the fact that in many networks roll-off tends towards a constant gradient at frequencies well away from the cut-off point of the frequency curve. Roll-off enables the cut-off performance of such a filter network to be reduced to a single number. Note that roll-o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Filter
Chebyshev filters are analog filter, analog or digital filter, digital filters that have a steeper roll-off than Butterworth filters, and have either passband ripple (filters), ripple (type I) or stopband ripple (type II). Chebyshev filters have the property that they minimize the error between the idealized and the actual filter characteristic over the operating frequency range of the filter, but they achieve this with ripples in the frequency response. This type of filter is named after Pafnuty Chebyshev because its mathematical characteristics are derived from Chebyshev polynomials. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters". Because of the passband ripple inherent in Chebyshev filters, filters with a smoother response in the passband but a more irregular response in the stopband are preferred for certain applications. Type I Chebyshev filters (Chebyshev filters) Type I Chebys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Filter
An elliptic filter (also known as a Cauer filter, named after Wilhelm Cauer, or as a Zolotarev filter, after Yegor Zolotarev) is a filter (signal processing), signal processing filter with equalized ripple (filters), ripple (equiripple) behavior in both the passband and the stopband. The amount of ripple in each band is independently adjustable, and no other filter of equal order can have a faster transition in Gain (electronics), gain between the passband and the stopband, for the given values of ripple (whether the ripple is equalized or not). Alternatively, one may give up the ability to adjust independently the passband and stopband ripple, and instead design a filter which is maximally insensitive to component variations. As the ripple in the stopband approaches zero, the filter becomes a type I Chebyshev filter. As the ripple in the passband approaches zero, the filter becomes a type II Chebyshev filter and finally, as both ripple values approach zero, the filter becomes a B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |