Convolution kernel on:
[Wikipedia]
[Google]
[Amazon]
F(s) = \int_^\infty e^ \ f(u) \ \textu
and
: G(s) = \int_^\infty e^ \ g(v) \ \textv
respectively, the convolution operation (f * g)(t) can be defined as the inverse Laplace transform of the product of F(s) and G(s) . More precisely,
:
\begin
F(s) \cdot G(s) &= \int_^\infty e^ \ f(u) \ \textu \cdot \int_^\infty e^ \ g(v) \ \textv \\
&= \int_^\infty \int_^\infty e^ \ f(u) \ g(v) \ \textu \ \textv
\end
Let t = u + v , then
:
\begin
F(s) \cdot G(s) &= \int_^\infty \int_^\infty e^ \ f(u) \ g(t - u) \ \textu \ \textt \\
&= \int_^\infty e^ \underbrace_ \ \textt \\
&= \int_^\infty e^ (f * g)(t) \ \textt.
\end
Note that F(s) \cdot G(s) is the bilateral Laplace transform of (f * g)(t) . A similar derivation can be done using the unilateral Laplace transform (one-sided Laplace transform).
The convolution operation also describes the output (in terms of the input) of an important class of operations known as ''linear time-invariant'' (LTI). See
\int f(u)\cdot g(x - u) \, du
is used by Sylvestre François Lacroix on page 505 of his book entitled ''Treatise on differences and series'', which is the last of 3 volumes of the encyclopedic series: , Chez Courcier, Paris, 1797–1800. Soon thereafter, convolution operations appear in the works of \int_0^t \varphi(s)\psi(t - s) \, ds,\quad 0 \le t < \infty,
is a particular case of composition products considered by the Italian mathematician
g_T is periodic, with period T , then for functions, f , such that f * g_T exists, the convolution is also periodic and identical to:
:(f * g_T)(t) \equiv \int_^ \left sum_^\infty f(\tau + kT)\rightg_T(t - \tau)\, d\tau,
where t_0 is an arbitrary choice. The summation is called a f .
When g_T is a periodic summation of another function, g , then f*g_T is known as a ''circular'' or ''cyclic'' convolution of f and g .
And if the periodic summation above is replaced by f_T , the operation is called a ''periodic'' convolution of f_T and g_T .
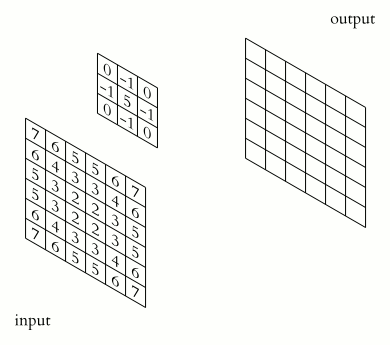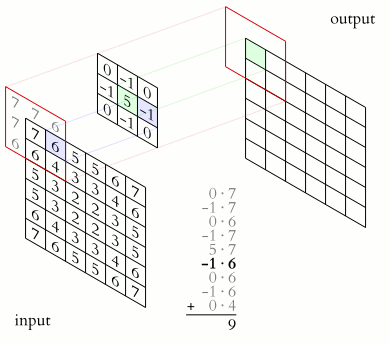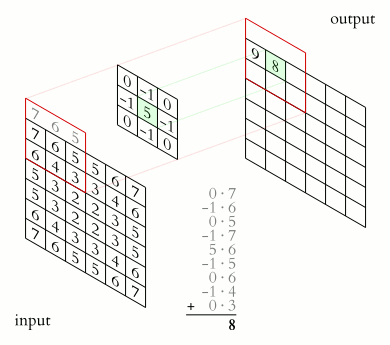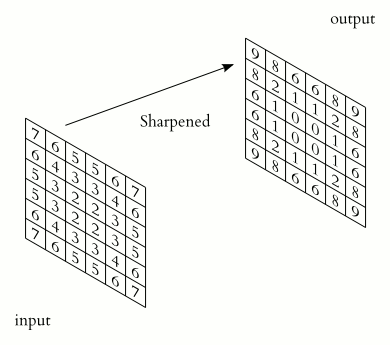 For complex-valued functions
For complex-valued functions f and g defined on the set \Z of integers, the ''discrete convolution'' of f and g is given by:
:(f * g) = \sum_^\infty f g - m
or equivalently (see (f * g) = \sum_^\infty f -mg
The convolution of two finite sequences is defined by extending the sequences to finitely supported functions on the set of integers. When the sequences are the coefficients of two \ (representing, for instance, a (f * g) \sum_^M f -m
g_ is periodic, with period N, then for functions, f, such that f*g_ exists, the convolution is also periodic and identical to:
:(f * g_) \equiv \sum_^ \left(\sum_^\infty + kNright) g_ - m
The summation on k is called a f.
If g_ is a periodic summation of another function, g, then f*g_ is known as a circular convolution of f and g.
When the non-zero durations of both f and g are limited to the interval ,N-1 f*g_ reduces to these common forms:
The notation f *_N g for ''cyclic convolution'' denotes convolution over the
(f * g )(x) = \int_ f(y)g(x-y)\,dy = \int_ f(x-y)g(y)\,dy,
and is well-defined only if and decay sufficiently rapidly at infinity in order for the integral to exist. Conditions for the existence of the convolution may be tricky, since a blow-up in at infinity can be easily offset by sufficiently rapid decay in . The question of existence thus may involve different conditions on and :
\, * g\, _p\le \, f\, _1\, g\, _p.
In the particular case , this shows that is a \frac+\frac=\frac+1,
then
:\left\Vert f*g\right\Vert_r\le\left\Vert f\right\Vert_p\left\Vert g\right\Vert_q,\quad f\in L^p,\ g\in L^q,
so that the convolution is a continuous bilinear mapping from to .
The Young inequality for convolution is also true in other contexts (circle group, convolution on ). The preceding inequality is not sharp on the real line: when , there exists a constant such that:
:\left\Vert f*g\right\Vert_r\le B_\left\Vert f\right\Vert_p\left\Vert g\right\Vert_q,\quad f\in L^p,\ g\in L^q.
The optimal value of was discovered in 1975 and independently in 1976, see \, f * g\, _r\le C_\, f\, _p\, g\, _
where \, g\, _ is the weak norm. Convolution also defines a bilinear continuous map L^\times L^\to L^ for 1< p,q,r<\infty , owing to the weak Young inequality:
:\, f * g\, _\le C_\, f\, _\, g\, _.
\int_ (y)g(x-y)\,dy = (f*g)(x) \in C^\infty(\mathbb^d) .
More generally, it is possible to extend the definition of the convolution in a unique way with \varphi the same as ''f'' above, so that the associative law
:f* (g* \varphi) = (f* g)* \varphi
remains valid in the case where ''f'' is a distribution, and ''g'' a compactly supported distribution .
\mu*\nu defined by
:\int_ f(x) \, d(\mu*\nu)(x) = \int_\int_f(x+y)\,d\mu(x)\,d\nu(y).
In particular,
: (\mu*\nu)(A) = \int_1_A(x+y)\, d(\mu\times\nu)(x,y),
where A\subset\mathbf R^d is a measurable set and 1_A is the A .
This agrees with the convolution defined above when μ and ν are regarded as distributions, as well as the convolution of L1 functions when μ and ν are absolutely continuous with respect to the Lebesgue measure.
The convolution of measures also satisfies the following version of Young's inequality
:\, \mu* \nu\, \le \, \mu\, \, \nu\,
where the norm is the
f * g = g * f Proof: By definition: (f * g)(t) = \int^\infty_ f(\tau)g(t - \tau)\, d\tau Changing the variable of integration to u = t - \tau the result follows.
; f * (g * h) = (f * g) * h Proof: This follows from using f * (g + h) = (f * g) + (f * h) Proof: This follows from linearity of the integral.
; Associativity with scalar multiplication: a (f * g) = (a f) * g for any real (or complex) number a .
; f * \delta = f where ''δ'' is the delta distribution.
; Inverse element: Some distributions ''S'' have an S^ * S = \delta from which an explicit formula for ''S''−1 may be obtained.The set of invertible distributions forms an \overline = \overline * \overline
; Time reversal: If q(t) = r(t)*s(t), then q(-t) = r(-t)*s(-t).
(f * g)' = f' * g = f * g' Proof:
:
\begin
(f * g)' & = \frac \int^\infty_ f(\tau) g(t - \tau) \, d\tau \\
& =\int^\infty_ f(\tau) \frac g(t - \tau) \, d\tau \\
& =\int^\infty_ f(\tau) g'(t - \tau) \, d\tau = f* g'.
\end
; Relationship with integration: If F(t) = \int^t_ f(\tau) d\tau, and G(t) = \int^t_ g(\tau) \, d\tau, then (F * g)(t) = (f * G)(t) = \int^t_(f * g)(\tau)\,d\tau.
\int_(f * g)(x) \, dx=\left(\int_f(x) \, dx\right) \left(\int_g(x) \, dx\right).
This follows from
\frac(f * g) = \frac * g = f * \frac
where \frac is the \frac(f * g) = \frac * g = f * \frac.
A particular consequence of this is that the convolution can be viewed as a "smoothing" operation: the convolution of ''f'' and ''g'' is differentiable as many times as ''f'' and ''g'' are in total.
These identities hold for example under the condition that ''f'' and ''g'' are absolutely integrable and at least one of them has an absolutely integrable (L1) weak derivative, as a consequence of Young's convolution inequality. For instance, when ''f'' is continuously differentiable with compact support, and ''g'' is an arbitrary locally integrable function,
: \frac(f* g) = \frac * g.
These identities also hold much more broadly in the sense of tempered distributions if one of ''f'' or ''g'' is a
rapidly decreasing tempered distribution, a
compactly supported tempered distribution or a Schwartz function and the other is a tempered distribution. On the other hand, two positive integrable and infinitely differentiable functions may have a nowhere continuous convolution.
In the discrete case, the D(f * g) = (Df) * g = f * (Dg).
\mathcal\ = \mathcal\\cdot \mathcal\
where \mathcal\ denotes the f .
\mathcal W is the Fourier transform matrix, then
: \mathcal W\left(C^x \ast C^y\right) = \left(\mathcal W C^ \bull \mathcal W C^\right)(x \otimes y) = \mathcal W C^x \circ \mathcal W C^y ,
where \bull is face-splitting product, \otimes denotes \circ denotes Hadamard product (this result is an evolving of count sketch properties).
This can be generalized for appropriate matrices \mathbf,\mathbf :
: \mathcal W\left((\mathbfx) \ast (\mathbfy)\right) = \left((\mathcal W \mathbf) \bull (\mathcal W \mathbf)\right)(x \otimes y) = (\mathcal W \mathbfx) \circ (\mathcal W \mathbfy)
from the properties of the face-splitting product.
\tau_x (f * g) = (\tau_x f) * g = f * (\tau_x g)
where τ''x''f is the translation of the function ''f'' by ''x'' defined by
: (\tau_x f)(y) = f(y - x).
If ''f'' is a
(f * g)(x) = \int_G f(y) g\left(y^x\right)\,d\lambda(y).
It is not commutative in general. In typical cases of interest ''G'' is a \int f\left(xy^\right)g(y) \, d\lambda(y) . The preference of one over the other is made so that convolution with a fixed function ''g'' commutes with left translation in the group:
:L_h(f* g) = (L_hf)* g.
Furthermore, the convention is also required for consistency with the definition of the convolution of measures given below. However, with a right instead of a left Haar measure, the latter integral is preferred over the former.
On locally compact abelian groups, a version of the T (x) = \frac \int_ (y) g( x - y) \, dy.
The operator ''T'' is \bar(-y).
By the commutativity property cited above, ''T'' is normal: ''T''* ''T'' = ''TT''* . Also, ''T'' commutes with the translation operators. Consider the family ''S'' of operators consisting of all such convolutions and the translation operators. Then ''S'' is a commuting family of normal operators. According to h_k (x) = e^, \quad k \in \mathbb,\;
which are precisely the characters of T. Each convolution is a compact
(\mu * \nu)(E) = \iint 1_E(xy) \,d\mu(x) \,d\nu(y)
for each measurable subset ''E'' of ''G''. The convolution is also a Radon measure, whose \, \mu * \nu\, \le \left\, \mu\right\, \left\, \nu\right\, .
In the case when ''G'' is
+\infty ) f_1,\dots,f_m on \mathbb R^n is defined by:
(f_1*\cdots*f_m)(x)=\inf_x \.
It can be shown that the infimal convolution of convex functions is convex. Furthermore, it satisfies an identity analogous to that of the Fourier transform of a traditional convolution, with the role of the Fourier transform is played instead by the Legendre transform:
\varphi^*(x) = \sup_y ( x\cdot y - \varphi(y)).
We have:
(f_1*\cdots *f_m)^*(x) = f_1^*(x) + \cdots + f_m^*(x).
X \mathrel X \otimes X \mathrel X \otimes X \mathrel X.
The convolution appears notably in the definition of S * \operatorname_X = \operatorname_X * S = \eta\circ\varepsilon.
i , some physical quantity A_i is calculated as a convolution of A_j with a weighting function, where j denotes the neighbors of particle i : those that are located within its kernel. The convolution is approximated as a summation over each neighbor.
* In
Earliest Uses: The entry on Convolution has some historical information.
o
* https://jhu.edu/~signals/convolve/index.html Visual convolution Java Applet * https://jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for discrete-time functions * https://get-the-solution.net/projects/discret-convolution discret-convolution online calculator *https://lpsa.swarthmore.edu/Convolution/CI.html Convolution demo and visualization in JavaScript *https://phiresky.github.io/convolution-demo/ Another convolution demo in JavaScript * Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters * https://archive.org/details/Lectures_on_Image_Processing
Convolution Kernel Mask Operation Interactive tutorial
at
Freeverb3 Impulse Response Processor
Opensource zero latency impulse response processor with VST plugins * Stanford University CS 17
showing how spatial convolution works.
A video lecture on the subject of convolution
given by Salman Khan
Example of FFT convolution for pattern-recognition (image processing)Intuitive Guide to Convolution
A blogpost about an intuitive interpretation of convolution. {{Artificial intelligence navbox Functional analysis Image processing Fourier analysis Bilinear maps Feature detection (computer vision)
In
s (two-sided Laplace transform)
:mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
(in particular, functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics ...
), convolution is a mathematical operation
In mathematics, an operation is a function from a set to itself. For example, an operation on real numbers will take in real numbers and return a real number. An operation can take zero or more input values (also called "'' operands''" or "argu ...
on two functions and that produces a third function , as the integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
). Graphically, it expresses how the 'shape' of one function is modified by the other.
Some features of convolution are similar to cross-correlation
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used f ...
: for real-valued functions, of a continuous or discrete variable, convolution differs from cross-correlation only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued functions, the cross-correlation operator is the adjoint of the convolution operator.
Convolution has applications that include probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
, statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
, spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum.
Spectro ...
, signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
and image processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a pr ...
, geophysics
Geophysics () is a subject of natural science concerned with the physical processes and Physical property, properties of Earth and its surrounding space environment, and the use of quantitative methods for their analysis. Geophysicists conduct i ...
, engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, computer vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical ...
and differential equations.
The convolution can be defined for functions on Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
and other group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic iden ...
s (as algebraic structure
In mathematics, an algebraic structure or algebraic system consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplicatio ...
s). For example, periodic function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the t ...
s, such as the discrete-time Fourier transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values.
The DTFT is often used to analyze samples of a continuous function. The term ''discrete-time'' refers ...
, can be defined on a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
and convolved by periodic convolution
Circular convolution, also known as cyclic convolution, is a special case of periodic convolution, which is the convolution of two periodic functions that have the same period. Periodic convolution arises, for example, in the context of the disc ...
. (See row 18 at .) A ''discrete convolution'' can be defined for functions on the set of integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s.
Generalizations of convolution have applications in the field of numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ...
and numerical linear algebra
Numerical linear algebra, sometimes called applied linear algebra, is the study of how matrix operations can be used to create computer algorithms which efficiently and accurately provide approximate answers to questions in continuous mathemati ...
, and in the design and implementation of finite impulse response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impuls ...
filters in signal processing.
Computing the inverse of the convolution operation is known as deconvolution
In mathematics, deconvolution is the inverse of convolution. Both operations are used in signal processing and image processing. For example, it may be possible to recover the original signal after a filter (convolution) by using a deconvolution ...
.
Definition
The convolution of and is written , denoting the operator with the symbol . It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. As such, it is a particular kind ofintegral transform
In mathematics, an integral transform is a type of transform that maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily charac ...
:
:
An equivalent definition is (see commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
):
:
While the symbol is used above, it need not represent the time domain. At each , the convolution formula can be described as the area under the function weighted by the function shifted by the amount . As changes, the weighting function emphasizes different parts of the input function ; If is a positive value, then is equal to that slides or is shifted along the -axis toward the right (toward ) by the amount of , while if is a negative value, then is equal to that slides or is shifted toward the left (toward ) by the amount of .
For functions , supported on only LTI system theory
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly define ...
for a derivation of convolution as the result of LTI constraints. In terms of the Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
s of the input and output of an LTI operation, no new frequency components are created. The existing ones are only modified (amplitude and/or phase). In other words, the output transform is the pointwise product of the input transform with a third transform (known as a transfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible ...
). See Convolution theorem
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions (or signals) is the product of their Fourier transforms. More generally, convolution in one domain (e.g., time dom ...
for a derivation of that property of convolution. Conversely, convolution can be derived as the inverse Fourier transform of the pointwise product of two Fourier transforms.
Visual explanation
Historical developments
One of the earliest uses of the convolution integral appeared inD'Alembert
Jean-Baptiste le Rond d'Alembert ( ; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanics, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the ''E ...
's derivation of Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the k-th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation a ...
in ''Recherches sur différents points importants du système du monde,'' published in 1754.
Also, an expression of the type:
:Pierre Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
, Jean-Baptiste Joseph Fourier, Siméon Denis Poisson
Baron Siméon Denis Poisson (, ; ; 21 June 1781 – 25 April 1840) was a French mathematician and physicist who worked on statistics, complex analysis, partial differential equations, the calculus of variations, analytical mechanics, electricity ...
, and others. The term itself did not come into wide use until the 1950s or 1960s. Prior to that it was sometimes known as ''Faltung'' (which means ''folding'' in German), ''composition product'', ''superposition integral'', and '' Carson's integral''. Yet it appears as early as 1903, though the definition is rather unfamiliar in older uses.
The operation:
:Vito Volterra
Vito Volterra (, ; 3 May 1860 – 11 October 1940) was an Italian mathematician and physicist, known for his contributions to Mathematical and theoretical biology, mathematical biology and Integral equation, integral equations, being one of the ...
in 1913.
Circular convolution
When a functionperiodic summation
In mathematics, any integrable function s(t) can be made into a periodic function s_P(t) with period ''P'' by summing the translations of the function s(t) by integer multiples of ''P''. This is called periodic summation:
:s_P(t) = \sum_^\inf ...
of the function Discrete convolution
 For complex-valued functions
For complex-valued functions commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
) by:
:polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ...
s, then the coefficients of the ordinary product of the two polynomials are the convolution of the original two sequences. This is known as the Cauchy product
In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin-Louis Cauchy.
Definitions
The Cauchy product may apply to infin ...
of the coefficients of the sequences.
Thus when has finite support in the set finite impulse response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impuls ...
), a finite summation may be used:
:Circular discrete convolution
When a functionperiodic summation
In mathematics, any integrable function s(t) can be made into a periodic function s_P(t) with period ''P'' by summing the translations of the function s(t) by integer multiples of ''P''. This is called periodic summation:
:s_P(t) = \sum_^\inf ...
of the function cyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
of integers modulo .
Circular convolution arises most often in the context of fast convolution with a fast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
(FFT) algorithm.
Fast convolution algorithms
In many situations, discrete convolutions can be converted to circular convolutions so that fast transforms with a convolution property can be used to implement the computation. For example, convolution of digit sequences is the kernel operation inmultiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
of multi-digit numbers, which can therefore be efficiently implemented with transform techniques (; ).
requires arithmetic operations per output value and operations for outputs. That can be significantly reduced with any of several fast algorithms. Digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a ...
and other applications typically use fast convolution algorithms to reduce the cost of the convolution to O( log ) complexity.
The most common fast convolution algorithms use fast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
(FFT) algorithms via the circular convolution theorem. Specifically, the circular convolution of two finite-length sequences is found by taking an FFT of each sequence, multiplying pointwise, and then performing an inverse FFT. Convolutions of the type defined above are then efficiently implemented using that technique in conjunction with zero-extension and/or discarding portions of the output. Other fast convolution algorithms, such as the Schönhage–Strassen algorithm or the Mersenne transform, use fast Fourier transforms in other ring
(The) Ring(s) may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
Arts, entertainment, and media Film and TV
* ''The Ring'' (franchise), a ...
s. The Winograd method is used as an alternative to the FFT. It significantly speeds up 1D, 2D, and 3D convolution.
If one sequence is much longer than the other, zero-extension of the shorter sequence and fast circular convolution is not the most computationally efficient method available. Instead, decomposing the longer sequence into blocks and convolving each block allows for faster algorithms such as the overlap–save method and overlap–add method
In signal processing, the overlap–add method is an efficient way to evaluate the discrete convolution of a very long signal x /math> with a finite impulse response (FIR) filter h /math>:
where h = 0 for m outside the region ,M This a ...
. A hybrid convolution method that combines block and FIR
Firs are evergreen coniferous trees belonging to the genus ''Abies'' () in the family Pinaceae. There are approximately 48–65 extant species, found on mountains throughout much of North and Central America, Eurasia, and North Africa. The genu ...
algorithms allows for a zero input-output latency that is useful for real-time convolution computations.
Domain of definition
The convolution of two complex-valued functions on is itself a complex-valued function on , defined by: :Compactly supported functions
If and arecompactly supported
In mathematics, the support of a real-valued function f is the subset of the function domain of elements that are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set ...
continuous function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More preci ...
s, then their convolution exists, and is also compactly supported and continuous . More generally, if either function (say ) is compactly supported and the other is locally integrable
In mathematics, a locally integrable function (sometimes also called locally summable function) is a function which is integrable (so its integral is finite) on every compact subset of its domain of definition. The importance of such functions li ...
, then the convolution is well-defined and continuous.
Convolution of and is also well defined when both functions are locally square integrable on and supported on an interval of the form (or both supported on ).
Integrable functions
The convolution of and exists if and are both Lebesgue integrable functions in (), and in this case is also integrable . This is a consequence of Tonelli's theorem. This is also true for functions in , under the discrete convolution, or more generally for the convolution on any group. Likewise, if () and () where , then (), and :Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers (or over a non-Archimedean complete normed field) that at the same time is also a Banach sp ...
under the convolution (and equality of the two sides holds if and are non-negative almost everywhere).
More generally, Young's inequality implies that the convolution is a continuous bilinear map between suitable spaces. Specifically, if satisfy:
:Brascamp–Lieb inequality In mathematics, the Brascamp–Lieb inequality is either of two inequalities. The first is a result in geometry concerning integrable functions on ''n''-dimensional Euclidean space \mathbb^. It generalizes the Loomis–Whitney inequality and Hölde ...
.
A stronger estimate is true provided :
:Functions of rapid decay
In addition to compactly supported functions and integrable functions, functions that have sufficiently rapid decay at infinity can also be convolved. An important feature of the convolution is that if ''f'' and ''g'' both decay rapidly, then ''f''∗''g'' also decays rapidly. In particular, if ''f'' and ''g'' arerapidly decreasing function In mathematics, a function is said to vanish at infinity if its values approach 0 as the input grows without bounds. There are two different ways to define this with one definition applying to functions defined on normed vector spaces and the other ...
s, then so is the convolution ''f''∗''g''. Combined with the fact that convolution commutes with differentiation (see #Properties), it follows that the class of Schwartz function
In mathematics, Schwartz space \mathcal is the function space of all functions whose derivatives are rapidly decreasing. This space has the important property that the Fourier transform is an automorphism on this space. This property enables ...
s is closed under convolution .
Distributions
If ''f'' is a smooth function that iscompactly supported
In mathematics, the support of a real-valued function f is the subset of the function domain of elements that are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set ...
and ''g'' is a distribution, then ''f''∗''g'' is a smooth function defined by
:Measures
The convolution of any twoBorel measure
In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets (and thus on all Borel sets). Some authors require additional restrictions on the measure, as described below.
...
s ''μ'' and ''ν'' of bounded variation
In mathematical analysis, a function of bounded variation, also known as ' function, is a real number, real-valued function (mathematics), function whose total variation is bounded (finite): the graph of a function having this property is well beh ...
is the measure indicator function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , then the indicator functio ...
of total variation
In mathematics, the total variation identifies several slightly different concepts, related to the (local property, local or global) structure of the codomain of a Function (mathematics), function or a measure (mathematics), measure. For a real ...
of a measure. Because the space of measures of bounded variation is a Banach space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and ...
, convolution of measures can be treated with standard methods of functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics ...
that may not apply for the convolution of distributions.
Properties
Algebraic properties
The convolution defines a product on the linear space of integrable functions. This product satisfies the following algebraic properties, which formally mean that the space of integrable functions with the product given by convolution is a commutativeassociative algebra
In mathematics, an associative algebra ''A'' over a commutative ring (often a field) ''K'' is a ring ''A'' together with a ring homomorphism from ''K'' into the center of ''A''. This is thus an algebraic structure with an addition, a mult ...
without identity . Other linear spaces of functions, such as the space of continuous functions of compact support, are closed under the convolution, and so also form commutative associative algebras.
; Commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
: Associativity
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replaceme ...
: Fubini's theorem
In mathematical analysis, Fubini's theorem characterizes the conditions under which it is possible to compute a double integral by using an iterated integral. It was introduced by Guido Fubini in 1907. The theorem states that if a function is L ...
(i.e., double integrals can be evaluated as iterated integrals in either order).
; Distributivity
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary ...
: Multiplicative identity
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
: No algebra of functions possesses an identity for the convolution. The lack of identity is typically not a major inconvenience, since most collections of functions on which the convolution is performed can be convolved with a delta distribution (a unitary impulse, centered at zero) or, at the very least (as is the case of ''L''1) admit approximations to the identity. The linear space of compactly supported distributions does, however, admit an identity under the convolution. Specifically, inverse element
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
''S''−1 for the convolution which then must satisfy abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commu ...
under the convolution.
; Complex conjugation: Proof (using; Relationship with differentiation:convolution theorem In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions (or signals) is the product of their Fourier transforms. More generally, convolution in one domain (e.g., time dom ...):q(t) \ \stackrel\ \ Q(f) = R(f)S(f) q(-t) \ \stackrel\ \ Q(-f) = R(-f)S(-f) \begin q(-t) &= \mathcal^\bigg\\\ &= \mathcal^\bigg\ * \mathcal^\bigg\\\ &= r(-t) * s(-t) \end
Integration
If ''f'' and ''g'' are integrable functions, then the integral of their convolution on the whole space is simply obtained as the product of their integrals: :Fubini's theorem
In mathematical analysis, Fubini's theorem characterizes the conditions under which it is possible to compute a double integral by using an iterated integral. It was introduced by Guido Fubini in 1907. The theorem states that if a function is L ...
. The same result holds if ''f'' and ''g'' are only assumed to be nonnegative measurable functions, by Tonelli's theorem.
Differentiation
In the one-variable case, :derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
. More generally, in the case of functions of several variables, an analogous formula holds with the partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
:
: difference operator
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
''D'' ''f''(''n'') = ''f''(''n'' + 1) − ''f''(''n'') satisfies an analogous relationship:
: Convolution theorem
Theconvolution theorem
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions (or signals) is the product of their Fourier transforms. More generally, convolution in one domain (e.g., time dom ...
states that
: Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
of Convolution in other types of transformations
Versions of this theorem also hold for theLaplace transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a f ...
, two-sided Laplace transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform equivalent to probability's moment-generating function. Two-sided Laplace transforms are closely related to the Fourier transform, the Melli ...
, Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain (the z-domain or z-plane) representation.
It can be considered a dis ...
and Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is
often used ...
.
Convolution on matrices
IfKronecker product
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vector ...
, Translational equivariance
The convolution commutes with translations, meaning that :Schwartz function
In mathematics, Schwartz space \mathcal is the function space of all functions whose derivatives are rapidly decreasing. This space has the important property that the Fourier transform is an automorphism on this space. This property enables ...
, then ''τxf'' is the convolution with a translated Dirac delta function ''τ''''x''''f'' = ''f'' ∗ ''τ''''x'' ''δ''. So translation invariance of the convolution of Schwartz functions is a consequence of the associativity of convolution.
Furthermore, under certain conditions, convolution is the most general translation invariant operation. Informally speaking, the following holds
: Suppose that ''S'' is a bounded linear operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pr ...
acting on functions which commutes with translations: ''S''(''τxf'') = ''τx''(''Sf'') for all ''x''. Then ''S'' is given as convolution with a function (or distribution) ''g''''S''; that is ''Sf'' = ''g''''S'' ∗ ''f''.
Thus some translation invariant operations can be represented as convolution. Convolutions play an important role in the study of time-invariant system
In control theory, a time-invariant (TI) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a ...
s, and especially LTI system theory
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly define ...
. The representing function ''g''''S'' is the impulse response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reac ...
of the transformation ''S''.
A more precise version of the theorem quoted above requires specifying the class of functions on which the convolution is defined, and also requires assuming in addition that ''S'' must be a continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces.
An operator between two normed spaces is a bounded linear ...
with respect to the appropriate topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
. It is known, for instance, that every continuous translation invariant continuous linear operator on ''L''1 is the convolution with a finite Borel measure
In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets (and thus on all Borel sets). Some authors require additional restrictions on the measure, as described below.
...
. More generally, every continuous translation invariant continuous linear operator on ''L''''p'' for 1 ≤ ''p'' < ∞ is the convolution with a tempered distribution
Distributions, also known as Schwartz distributions are a kind of generalized function in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, an ...
whose Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
is bounded. To wit, they are all given by bounded Fourier multiplier
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a speci ...
s.
Convolutions on groups
If ''G'' is a suitablegroup
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic iden ...
endowed with a measure λ, and if ''f'' and ''g'' are real or complex valued integrable functions on ''G'', then we can define their convolution by
:locally compact
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which e ...
Hausdorff topological group
In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures ...
and λ is a (left-) Haar measure
In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral for functions on those groups.
This Measure (mathematics), measure was introduced by Alfr� ...
. In that case, unless ''G'' is unimodular, the convolution defined in this way is not the same as convolution theorem
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions (or signals) is the product of their Fourier transforms. More generally, convolution in one domain (e.g., time dom ...
holds: the Fourier transform of a convolution is the pointwise product of the Fourier transforms. The circle group
In mathematics, the circle group, denoted by \mathbb T or , is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers
\mathbb T = \.
The circle g ...
T with the Lebesgue measure is an immediate example. For a fixed ''g'' in ''L''1(T), we have the following familiar operator acting on the Hilbert space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The ...
''L''2(T):
:compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
. A direct calculation shows that its adjoint ''T* '' is convolution with
:spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operator (mathematics), operators in a variety of mathematical ...
, there exists an orthonormal basis that simultaneously diagonalizes ''S''. This characterizes convolutions on the circle. Specifically, we have
:multiplication operator
In operator theory, a multiplication operator is a linear operator defined on some vector space of functions and whose value at a function is given by multiplication by a fixed function . That is,
T_f\varphi(x) = f(x) \varphi (x) \quad
for all ...
in this basis. This can be viewed as a version of the convolution theorem discussed above.
A discrete example is a finite cyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
of order ''n''. Convolution operators are here represented by circulant matrices, and can be diagonalized by the discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
.
A similar result holds for compact groups (not necessarily abelian): the matrix coefficients of finite-dimensional unitary representation
In mathematics, a unitary representation of a group ''G'' is a linear representation π of ''G'' on a complex Hilbert space ''V'' such that π(''g'') is a unitary operator for every ''g'' ∈ ''G''. The general theory is well-developed in the ca ...
s form an orthonormal basis in ''L''2 by the Peter–Weyl theorem
In mathematics, the Peter–Weyl theorem is a basic result in the theory of harmonic analysis, applying to topological groups that are Compact group, compact, but are not necessarily Abelian group, abelian. It was initially proved by Hermann Weyl, ...
, and an analog of the convolution theorem continues to hold, along with many other aspects of harmonic analysis
Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on unbounded do ...
that depend on the Fourier transform.
Convolution of measures
Let ''G'' be a (multiplicatively written) topological group. If μ and ν areRadon measure
In mathematics (specifically in measure theory), a Radon measure, named after Johann Radon, is a measure on the -algebra of Borel sets of a Hausdorff topological space that is finite on all compact sets, outer regular on all Borel sets, and ...
s on ''G'', then their convolution ''μ''∗''ν'' is defined as the pushforward measure
In measure theory, a pushforward measure (also known as push forward, push-forward or image measure) is obtained by transferring ("pushing forward") a measure from one measurable space to another using a measurable function.
Definition
Given mea ...
of the group action
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S.
Many sets of transformations form a group under ...
and can be written as
:total variation
In mathematics, the total variation identifies several slightly different concepts, related to the (local property, local or global) structure of the codomain of a Function (mathematics), function or a measure (mathematics), measure. For a real ...
satisfies
:locally compact
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which e ...
with (left-)Haar measure
In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral for functions on those groups.
This Measure (mathematics), measure was introduced by Alfr� ...
λ, and μ and ν are absolutely continuous
In calculus and real analysis, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship betwe ...
with respect to a λ, so that each has a density function, then the convolution μ∗ν is also absolutely continuous, and its density function is just the convolution of the two separate density functions. In fact, if ''either'' measure is absolutely continuous with respect to the Haar measure, then so is their convolution.
If μ and ν are probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure an ...
s on the topological group then the convolution ''μ''∗''ν'' is the probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
of the sum ''X'' + ''Y'' of two independent
Independent or Independents may refer to:
Arts, entertainment, and media Artist groups
* Independents (artist group), a group of modernist painters based in Pennsylvania, United States
* Independentes (English: Independents), a Portuguese artist ...
random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s ''X'' and ''Y'' whose respective distributions are μ and ν.
Infimal convolution
Inconvex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex optimization, convex minimization, a subdomain of optimization (mathematics), optimization theor ...
, the infimal convolution of proper (not identically convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
s Bialgebras
Let (''X'', Δ, ∇, ''ε'', ''η'') be abialgebra
In mathematics, a bialgebra over a Field (mathematics), field ''K'' is a vector space over ''K'' which is both a unital algebra, unital associative algebra and a coalgebra, counital coassociative coalgebra. The algebraic and coalgebraic structure ...
with comultiplication Δ, multiplication ∇, unit η, and counit ''ε''. The convolution is a product defined on the endomorphism algebra
In mathematics, the endomorphisms of an abelian group ''X'' form a ring. This ring is called the endomorphism ring of ''X'', denoted by End(''X''); the set of all homomorphisms of ''X'' into itself. Addition of endomorphisms arises naturally in a ...
End(''X'') as follows. Let ''φ'', ''ψ'' ∈ End(''X''), that is, ''φ'', ''ψ'': ''X'' → ''X'' are functions that respect all algebraic structure of ''X'', then the convolution ''φ''∗''ψ'' is defined as the composition
:Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously a ( unital associative) algebra and a (counital coassociative) coalgebra, with these structures' compatibility making it a bialgebra, and that moreover ...
s . A bialgebra is a Hopf algebra if and only if it has an antipode: an endomorphism ''S'' such that
:Applications
Convolution and related operations are found in many applications in science, engineering and mathematics. *Convolutional neural network
A convolutional neural network (CNN) is a type of feedforward neural network that learns features via filter (or kernel) optimization. This type of deep learning network has been applied to process and make predictions from many different ty ...
s apply multiple cascaded ''convolution'' kernels with applications in machine vision
Machine vision is the technology and methods used to provide image, imaging-based automation, automatic inspection and analysis for such applications as automatic inspection, process control, and robot guidance, usually in industry. Machine vision ...
and artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
. Though these are actually cross-correlations rather than convolutions in most cases.
* In non- neural-network-based image processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a pr ...
** In digital image processing
Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allo ...
convolutional filtering plays an important role in many important algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
s in edge detection
Edge or EDGE may refer to:
Technology Computing
* Edge computing, a network load-balancing system
* Edge device, an entry point to a computer network
* Adobe Edge, a graphical development application
* Microsoft Edge, a web browser developed b ...
and related processes (see Kernel (image processing))
** In optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
, an out-of-focus photograph is a convolution of the sharp image with a lens function. The photographic term for this is bokeh
In photography, bokeh ( or ; ) is the aesthetic quality of the blur produced in out-of-focus parts of an image, whether foreground or background or both. It is created by using a wide aperture lens.
Some photographers incorrectly restr ...
.
** In image processing applications such as adding blurring.
* In digital data processing
** In analytical chemistry
Analytical skill, Analytical chemistry studies and uses instruments and methods to Separation process, separate, identify, and Quantification (science), quantify matter. In practice, separation, identification or quantification may constitute t ...
, Savitzky–Golay smoothing filters are used for the analysis of spectroscopic data. They can improve signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in deci ...
with minimal distortion of the spectra
** In statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, a weighted moving average
In statistics, a moving average (rolling average or running average or moving mean or rolling mean) is a calculation to analyze data points by creating a series of averages of different selections of the full data set. Variations include: #Simpl ...
is a convolution.
* In acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
, reverberation
In acoustics, reverberation (commonly shortened to reverb) is a persistence of sound after it is produced. It is often created when a sound is reflection (physics), reflected on surfaces, causing multiple reflections that build up and then de ...
is the convolution of the original sound with echo
In audio signal processing and acoustics, an echo is a reflection of sound that arrives at the listener with a delay after the direct sound. The delay is directly proportional to the distance of the reflecting surface from the source and the lis ...
es from objects surrounding the sound source.
** In digital signal processing, convolution is used to map the impulse response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reac ...
of a real room on a digital audio signal.
** In electronic music
Electronic music broadly is a group of music genres that employ electronic musical instruments, circuitry-based music technology and software, or general-purpose electronics (such as personal computers) in its creation. It includes both music ...
convolution is the imposition of a spectral or rhythmic structure on a sound. Often this envelope or structure is taken from another sound. The convolution of two signals is the filtering of one through the other.Zölzer, Udo, ed. (2002). ''DAFX:Digital Audio Effects'', p.48–49. .
* In electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, the convolution of one function (the input signal) with a second function (the impulse response) gives the output of a linear time-invariant system
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of Linear system#Definition, linearity and Time-invariant system, ...
(LTI). At any given moment, the output is an accumulated effect of all the prior values of the input function, with the most recent values typically having the most influence (expressed as a multiplicative factor). The impulse response function provides that factor as a function of the elapsed time since each input value occurred.
* In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, wherever there is a linear system
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator.
Linear systems typically exhibit features and properties that are much simpler than the nonlinear case.
As a mathematical abstractio ...
with a "superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
", a convolution operation makes an appearance. For instance, in spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum.
Spectro ...
line broadening due to the Doppler effect on its own gives a Gaussian spectral line shape
Spectral line shape or spectral line profile describes the form of an electromagnetic spectrum in the vicinity of a spectral line – a region of stronger or weaker intensity in the spectrum. Ideal line shapes include Lorentz distribution, Lorent ...
and collision broadening alone gives a Lorentzian line shape. When both effects are operative, the line shape is a convolution of Gaussian and Lorentzian, a Voigt function.
** In time-resolved fluorescence spectroscopy, the excitation signal can be treated as a chain of delta pulses, and the measured fluorescence is a sum of exponential decays from each delta pulse.
** In computational fluid dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid dynamics, fluid flows. Computers are used to perform the calculations required ...
, the large eddy simulation
Large eddy simulation (LES) is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and first explored by Deardorff (1970). LES is ...
(LES) turbulence model uses the convolution operation to lower the range of length scales necessary in computation thereby reducing computational cost.
* In probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
, the probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
of the sum of two independent
Independent or Independents may refer to:
Arts, entertainment, and media Artist groups
* Independents (artist group), a group of modernist painters based in Pennsylvania, United States
* Independentes (English: Independents), a Portuguese artist ...
random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s is the convolution of their individual distributions.
** In kernel density estimation
In statistics, kernel density estimation (KDE) is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function of a random variable based on '' kernels'' as ...
, a distribution is estimated from sample points by convolution with a kernel, such as an isotropic Gaussian.
* In radiotherapy treatment planning systems, most part of all modern codes of calculation applies a convolution-superposition algorithm.
* In structural reliability, the reliability index can be defined based on the convolution theorem.
** The definition of reliability index for limit state functions with nonnormal distributions can be established corresponding to the joint distribution function. In fact, the joint distribution function can be obtained using the convolution theory.
* In Smoothed-particle hydrodynamics
Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and Fluid dynamics, fluid flows. It was developed by robert A. Gingold, Gingold and Joseph J. Monaghan ...
, simulations of fluid dynamics are calculated using particles, each with surrounding kernels. For any given particle Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D
D f(x) = \frac f(x)\,,
and of the integration ...
convolution is instrumental in various definitions of fractional integral and fractional derivative.
See also
* Analog signal processing *Circulant matrix
In linear algebra, a circulant matrix is a square matrix in which all rows are composed of the same elements and each row is rotated one element to the right relative to the preceding row. It is a particular kind of Toeplitz matrix.
In numerica ...
* Convolution for optical broad-beam responses in scattering media
* Convolution power
* Convolution quotient
* Deconvolution
In mathematics, deconvolution is the inverse of convolution. Both operations are used in signal processing and image processing. For example, it may be possible to recover the original signal after a filter (convolution) by using a deconvolution ...
* Dirichlet convolution
In mathematics, Dirichlet convolution (or divisor convolution) is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Peter Gustav Lejeune Dirichlet.
Definition
If f , g : \mathbb\to\mathbb ...
* Generalized signal averaging
* List of convolutions of probability distributions
* LTI system theory#Impulse response and convolution
* Multidimensional discrete convolution
In signal processing, multidimensional discrete convolution refers to the mathematical operation between two functions ''f'' and ''g'' on an ''n''-dimensional lattice that produces a third function, also of ''n''-dimensions. Multidimensional discre ...
* Scaled correlation
* Titchmarsh convolution theorem
* Toeplitz matrix (convolutions can be considered a Toeplitz matrix operation where each row is a shifted copy of the convolution kernel)
* Wavelet transform
Notes
References
Further reading
* . * * * Dominguez-Torres, Alejandro (Nov 2, 2010). "Origin and history of convolution". 41 pgs. https://slideshare.net/Alexdfar/origin-adn-history-of-convolution. Cranfield, Bedford MK43 OAL, UK. Retrieved Mar 13, 2013. * * * . * . * . * . * . * * * . * * . * . * . * . * * * .External links
Earliest Uses: The entry on Convolution has some historical information.
o
* https://jhu.edu/~signals/convolve/index.html Visual convolution Java Applet * https://jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for discrete-time functions * https://get-the-solution.net/projects/discret-convolution discret-convolution online calculator *https://lpsa.swarthmore.edu/Convolution/CI.html Convolution demo and visualization in JavaScript *https://phiresky.github.io/convolution-demo/ Another convolution demo in JavaScript * Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters * https://archive.org/details/Lectures_on_Image_Processing
Convolution Kernel Mask Operation Interactive tutorial
at
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science ...
Freeverb3 Impulse Response Processor
Opensource zero latency impulse response processor with VST plugins * Stanford University CS 17
showing how spatial convolution works.
A video lecture on the subject of convolution
given by Salman Khan
Example of FFT convolution for pattern-recognition (image processing)
A blogpost about an intuitive interpretation of convolution. {{Artificial intelligence navbox Functional analysis Image processing Fourier analysis Bilinear maps Feature detection (computer vision)