|
Sherwood Number
The Sherwood number (Sh) (also called the mass transfer Nusselt number) is a dimensionless number used in mass-transfer operation. It represents the ratio of the convective mass transfer to the rate of diffusive mass transport, and is named in honor of Thomas Kilgore Sherwood. It is defined as follows :\mathrm = \frac = \frac where * ''L'' is a characteristic length (m) * ''D'' is mass diffusivity (m2 s−1) * ''h'' is the convective mass transfer film coefficient (m s−1) Using dimensional analysis, it can also be further defined as a function of the Reynolds and Schmidt numbers: :\mathrm = f(\mathrm, \mathrm) For example, for a single sphere it can be expressed as: :\mathrm = \mathrm_0 + C\, \mathrm^\, \mathrm^ where \mathrm_0 is the Sherwood number due only to natural convection and not forced convection. A more specific correlation is the Froessling equation: :\mathrm = 2 + 0.552\, \mathrm^\, \mathrm^ This form is applicable to molecular diffusion from a sing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nusselt Number
In thermal fluid dynamics, the Nusselt number (, after Wilhelm Nusselt) is the ratio of convective to conductive heat transfer at a boundary in a fluid. Convection includes both advection (fluid motion) and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number. A Nusselt number of value one (zero) represents heat transfer by pure conduction. A value between one (zero) and 10 is characteristic of slug flow or laminar flow. A larger Nusselt number corresponds to more active convection, with turbulent flow typically in the 100–1000 range. A similar non-dimensional property is the Biot number, which concerns thermal conductivity for a solid body rather than a fluid. The mass transfer analogue of the Nusselt number is the Sherwood number. Definition The Nusselt number is the ratio of convective to conduct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Number
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the fie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
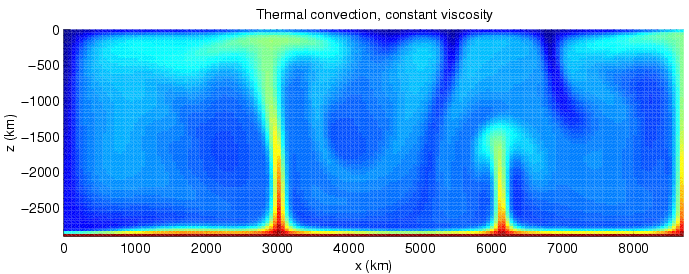
Convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see Convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often cate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Kilgore Sherwood
Thomas Kilgore Sherwood (July 25, 1903 – January 14, 1976) was a noted American chemical engineer and a founding member of the National Academy of Engineering. Biography Sherwood was born in Columbus, Ohio, and spent much of his youth in Montreal. In 1923 he received his B.S. from McGill University, and entered the Massachusetts Institute of Technology (MIT) for his Ph.D. His dissertation, "The Mechanism of the Drying of Solids," was completed in 1929, a year after he had become assistant professor at Worcester Polytechnic Institute. In 1930 he returned to MIT as assistant professor where he remained until his retirement, serving as associate professor (1933), professor (1941), and dean of engineering (1946–1952). In 1969 he retired from MIT to become professor of chemical engineering at the University of California, Berkeley. Sherwood's primary research area was mass transfer, and in 1937 he published the first major textbook in the field, ''Absorption and Extraction'' (r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Diffusivity
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of 16 mm2/s, and in water its diffusion coefficient is 0.0016 mm2/s. Diffusivity has dimensions of length2 / time, or m2/s in SI units and cm2/s in CGS units. Temperature dependence of the diffusion coefficient Solids The diffusion coefficient in solids at different temperatures is generally found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schmidt Number
Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975). The Schmidt number is the ratio of the shear component for diffusivity ''viscosity/density'' to the diffusivity for mass transfer ''D''. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer. It is defined as: :\mathrm = \frac = \frac = \frac where: * \nu is the kinematic viscosity or (/\,) in units of (m2/s) * D is the mass diffusivity (m2/s). * is the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/m·s) * \rho is the density of the fluid (kg/m3). The heat transfer analog of the Schmidt number is the Prandtl number (Pr). The ratio of thermal diffusivity to mass diffusivity is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as: : \mathrm = \frac = \frac = \frac = \frac where: * \nu : momentum diffusivity (kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Churchill–Bernstein Equation
In convective heat transfer, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for a Newtonian fluid. When the concentration and temperature profiles are independent of one another, the mass-heat transfer analogy can be employed. In the mass-heat transfer analogy, heat transfer dimensionless quantities are replaced with analogous mass transfer dimensionless quantities. This equation is named after Stuart W. Churchill and M. Bernstein, who introduced it in 1977. This equation is also called the Churchill–Bernstein correlation. Heat transfer definition :\overline_D \ = 0.3 + \frac\bigg + \bigg(\frac \bigg)^\bigg \quad \Pr\mathrm_D \ge 0.2 where: * \overline_D is the surface averaged Nusselt number with characteristic length of diameter; * \mathrm_D\,\! is the Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Numbers
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |