|
Secant Line
In geometry, a secant is a line (geometry), line that intersects a curve at a minimum of two distinct Point (geometry), points.. The word ''secant'' comes from the Latin word ''secare'', meaning ''to cut''. In the case of a circle, a secant intersects the circle at exactly two points. A Chord (geometry), chord is the line segment determined by the two points, that is, the interval (mathematics), interval on the secant whose ends are the two points. Circles A straight line can intersect a circle at zero, one, or two points. A line with intersections at two points is called a ''secant line'', at one point a ''tangent line'' and at no points an ''exterior line''. A ''chord'' is the line segment that joins two distinct points of a circle. A chord is therefore contained in a unique secant line and each secant line determines a unique chord. In rigorous modern treatments of plane geometry, results that seem obvious and were assumed (without statement) by Euclid in Euclid's Elements, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
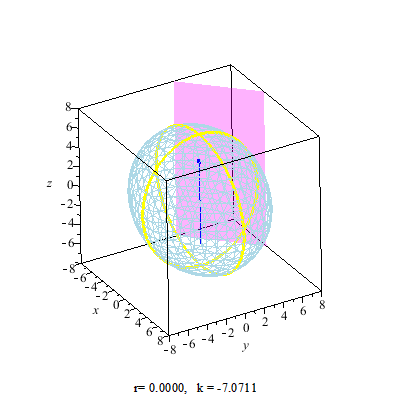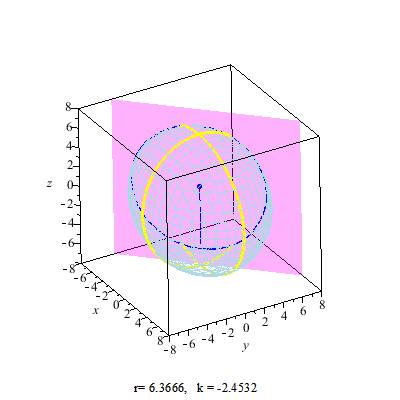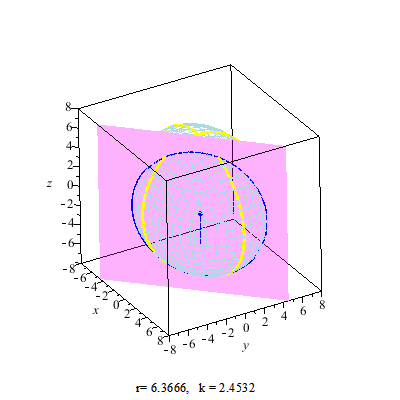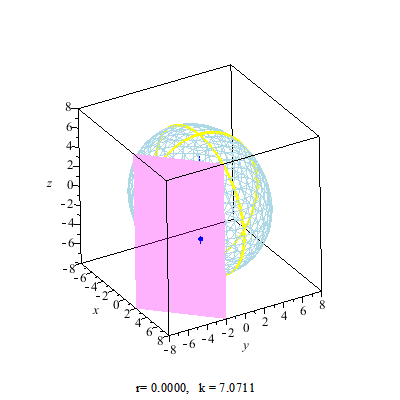
Secant Plane
A secant plane is a plane containing a nontrivial section of a sphere or an ellipsoid, or such a plane that a sphere is projected onto. Secant planes are similar to tangent planes, which contact the sphere's surface at a point, while secant planes contact the surface along curves. The two-dimensional representations of secant planes are secant lines, the lines that join two distinct points on a curve. Applications Secant planes are used in map projections. The secant plane intersects a globe along a small circle with no distortion, forming a standard parallel which has true scale. See also * Circular section * Circular segment * Spherical cap * Tangent space In mathematics, the tangent space of a manifold is a generalization of to curves in two-dimensional space and to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be ... References {{Reflist External links Tangents and Secants in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrisecant
In geometry, a quadrisecant or quadrisecant line of a space curve is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types: * Knots and links in knot theory, when nontrivial, always have quadrisecants, and the existence and number of quadrisecants has been studied in connection with knot invariants including the minimum total curvature and the ropelength of a knot. *The number of quadrisecants of a non-singular algebraic curve in complex projective space can be computed by a formula derived by Arthur Cayley. *Quadrisecants of arrangements of skew lines touch subsets of four lines from the arrangement. They are associated with ruled surfaces and the Schläfli double six configuration. Definition and motivation A quadrisecant is a line that intersects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Value Theorem
In mathematics, the mean value theorem (or Lagrange's mean value theorem) states, roughly, that for a given planar arc (geometry), arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant line, secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval (mathematics), interval starting from local hypotheses about derivatives at points of the interval. History A special case of this theorem for inverse interpolation of the sine was first described by Parameshvara (1380–1460), from the Kerala School of Astronomy and Mathematics in India, in his commentaries on Govindasvāmi and Bhāskara II. A restricted form of the theorem was proved by Michel Rolle in 1691; the result was what is now known as Rolle's theorem, and was proved only for polynomials, without the techniques of calculus. The mean value theorem in its modern for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which consists of solutions for: :y^2 = x^3 + ax + b for some coefficients and in . The curve is required to be non-singular, which means that the curve has no cusps or self-intersections. (This is equivalent to the condition , that is, being square-free in .) It is always understood that the curve is really sitting in the projective plane, with the point being the unique point at infinity. Many sources define an elliptic curve to be simply a curve given by an equation of this form. (When the coefficient field has characteristic 2 or 3, the above equation is not quite general enough to include all non-singular cubic cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orchard-planting Problem
In discrete geometry, the original orchard-planting problem (or the tree-planting problem) asks for the maximum number of 3-point lines attainable by a configuration of a specific number of points in the plane. There are also investigations into how many -point lines there can be. Hallard T. Croft and Paul Erdős proved t_k > \frac, where is the number of points and is the number of -point lines. Their construction contains some -point lines, where . One can also ask the question if these are not allowed. Integer sequence Define to be the maximum number of 3-point lines attainable with a configuration of points. For an arbitrary number of points, was shown to be \tfracn^2 - O(n) in 1974. The first few values of are given in the following table . Upper and lower bounds Since no two lines may share two distinct points, a trivial upper-bound for the number of 3-point lines determined by points is \left\lfloor \binom \Big/ \binom \right\rfloor = \left\lfloor \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collinearity
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row". Points on a line In any geometry, the set of points on a line are said to be collinear. In Euclidean geometry this relation is intuitively visualized by points lying in a row on a "straight line". However, in most geometries (including Euclidean) a line is typically a primitive (undefined) object type, so such visualizations will not necessarily be appropriate. A model for the geometry offers an interpretation of how the points, lines and other object types relate to one another and a notion such as collinearity must be interpreted within the context of that model. For instance, in spherical geometry, where lines are represented in the standard model by great circles of a spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester–Gallai Theorem
The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944. A line that contains exactly two of a set of points is known as an ''ordinary line''. Another way of stating the theorem is that every finite set of points that is not collinear has an ordinary line. According to a strengthening of the theorem, every finite point set (not all on one line) has at least a linear number of ordinary lines. An algorithm can find an ordinary line in a set of n points in time O(n\log n). History The Sylvester–Gallai theorem was posed as a problem by . suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry, in which the inflection points of a cubic curve i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object. Discrete geometry has a large overlap with convex geometry and computational geometry, and is closely related to subjects such as finite geometry, combinatorial optimization, digital geometry, discrete differential geometry, geometric graph theory, toric geometry, and combinatorial topology. History Polyhedra and tessellations had been studied for many years by people such as Kepler and Cauchy, modern discrete geometry has its origins in the late 19th century. Early topics s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incidence Geometry
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An ''incidence structure'' is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries. Incidence structures arise naturally and have been studied in various areas of mathematics. Consequently, there are different terminologies to describe these objects. In graph theory th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |