|
Repunit Prime
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book ''Recreations in the Theory of Numbers''. A repunit prime is a repunit that is also a prime number. Primes that are repunits in base-2 are Mersenne primes. As of October 2024, the largest known prime number , the largest probable prime ''R''8177207 and the largest elliptic curve primality-proven prime ''R''86453 are all repunits in various bases. Definition The base-''b'' repunits are defined as (this ''b'' can be either positive or negative) :R_n^\equiv 1 + b + b^2 + \cdots + b^ = \qquad\mbox, b, \ge2, n\ge1. Thus, the number ''R''''n''(''b'') consists of ''n'' copies of the digit 1 in base-''b'' representation. The first two repunits base-''b'' for ''n'' = 1 and ''n'' = 2 are :R_1^ 1 \qquad \text \qquad R_2^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
11 (number)
11 (eleven) is the natural number following 10 and preceding 12 (number), 12. It is the smallest number whose name has three syllables. Name "Eleven" derives from the Old English ', which is first attested in Bede's late 9th-century ''Ecclesiastical History of the English People''. It has cognates in every Germanic language (for example, German ), whose Proto-Germanic language, Proto-Germanic ancestor has been linguistic reconstruction, reconstructed as , from the prefix (adjectival "1 (number), one") and suffix , of uncertain meaning. It is sometimes compared with the Lithuanian language, Lithuanian ', though ' is used as the suffix for all numbers from 11 to 19. The Old English form has closer cognates in Old Frisian, Old Saxon, Saxon, and Old Norse, Norse, whose ancestor has been reconstructed as . This was formerly thought to be derived from Proto-Germanic ("10 (number), ten"); it is now sometimes connected with or ("left; remaining"), with the implicit meaning that "one is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coprime Integers
In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also ''is prime to'' or ''is coprime with'' . The numbers 8 and 9 are coprime, despite the fact that neither—considered individually—is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing When the integers and are coprime, the standard way of expressing this fact in mathematical notation is to indicate that their greatest common divisor is one, by the formula or . In their 1989 textbook ''Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed an alternative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
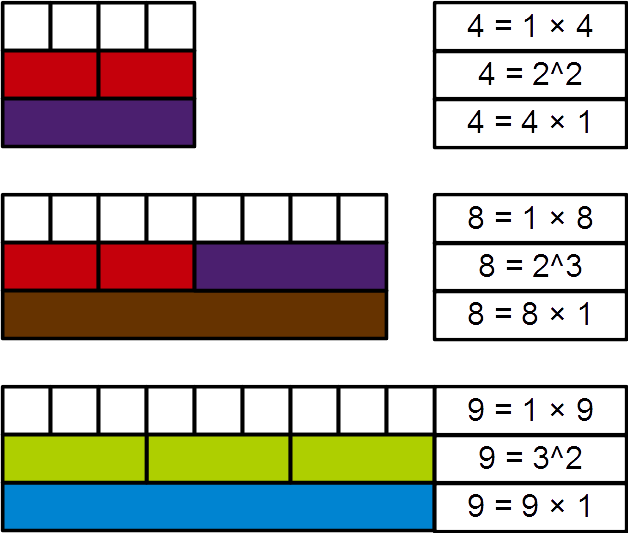
Prime Power
In mathematics, a prime power is a positive integer which is a positive integer power of a single prime number. For example: , and are prime powers, while , and are not. The sequence of prime powers begins: 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29, 31, 32, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 107, 109, 113, 121, 125, 127, 128, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 243, 251, … . The prime powers are those positive integers that are divisible by exactly one prime number; in particular, the number 1 is not a prime power. Prime powers are also called primary numbers, as in the primary decomposition. Properties Algebraic properties Prime powers are powers of prime numbers. Every prime power (except powers of 2 greater than 4) has a primitive root; thus the multiplicative group of integers modulo ''p''''n'' (that is, the group of units of the ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set can mean one of two different things: * an arrangement of its members in a sequence or linear order, or * the act or process of changing the linear order of an ordered set. An example of the first meaning is the six permutations (orderings) of the set : written as tuples, they are (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). Anagrams of a word whose letters are all different are also permutations: the letters are already ordered in the original word, and the anagram reorders them. The study of permutations of finite sets is an important topic in combinatorics and group theory. Permutations are used in almost every branch of mathematics and in many other fields of science. In computer science, they are used for analyzing sorting algorithms; in quantum physics, for describing states of particles; and in biology, for describing RNA sequences. The number of permutations of distinct objects is factorial, us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutable Prime
A permutable prime, also known as anagrammatic prime, is a prime number which, in a given radix, base, can have its digits' positions switched through any permutation and still be a prime number. H. E. Richert, who is supposedly the first to study these primes, called them permutable primes, but later they were also called absolute primes. Base 2 In base 2, only repunits can be permutable primes, because any 0 permuted to the ones place results in an even number. Therefore, the base 2 permutable primes are the Mersenne primes. The generalization can safely be made that for any positional number system, permutable primes with more than one digit can only have digits that are coprime with the radix of the number system. One-digit primes, meaning any prime below the radix, are always trivially permutable. Base 10 In base 10, all the permutable primes with fewer than 49,081 digits are known :2 (number), 2, 3 (number), 3, 5 (number), 5, 7 (number), 7, 11 (number), 11, 13 (number) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number Theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic analysis, asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function). The first such distribution found is , where is the prime-counting function (the number of primes less than or equal to ''N'') and is the natural logarithm of . This means that for large enough , the probability that a random integer not greater than is prime is very close to . Consequently, a random integer with at most digits (for large enough ) is about half as likely to be prime as a random integer with at most digits. For example, among the positive integers of at most 1000 digits, about on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Pages
The PrimePages is a website about prime number A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...s originally created by Chris Caldwell at the University of Tennessee at Martin who maintained it from 1994 to 2023. The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms. The PrimePages has articles on primes and primality testing. It includes "The Prime Glossary" with articles on hundreds of glosses related to primes, and "Prime Curios!" with thousands of curios about specific numbers. The database started as a list of "titanic primes" (primes with at least 1000 decimal digits) by Samuel Yates in 1984. On March 11, 2023, the PrimePages moved from primes.utm.edu to t5k.or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OEIS
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009, and is its chairman. OEIS records information on integer sequences of interest to both professional and amateur mathematicians, and is widely cited. , it contains over 370,000 sequences, and is growing by approximately 30 entries per day. Each entry contains the leading terms of the sequence, keywords, mathematical motivations, literature links, and more, including the option to generate a graph or play a musical representation of the sequence. The database is searchable by keyword, by subsequence, or by any of 16 fields. There is also an advanced search function called SuperSeeker which runs a large number of different algorithms to identify sequences related to the input. History Neil Sloane started coll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A004023
A, or a, is the first letter and the first vowel letter of the Latin alphabet, used in the modern English alphabet, and others worldwide. Its name in English is '' a'' (pronounced ), plural ''aes''. It is similar in shape to the Ancient Greek letter alpha, from which it derives. The uppercase version consists of the two slanting sides of a triangle, crossed in the middle by a horizontal bar. The lowercase version is often written in one of two forms: the double-storey and single-storey . The latter is commonly used in handwriting and fonts based on it, especially fonts intended to be read by children, and is also found in italic type. In English, '' a'' is the indefinite article, with the alternative form ''an''. Name In English, the name of the letter is the ''long A'' sound, pronounced . Its name in most other languages matches the letter's pronunciation in open syllables. History The earliest known ancestor of A is ''aleph''—the first letter of the Phoenician ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclotomic Polynomial
In mathematics, the ''n''th cyclotomic polynomial, for any positive integer ''n'', is the unique irreducible polynomial with integer coefficients that is a divisor of x^n-1 and is not a divisor of x^k-1 for any Its roots are all ''n''th primitive roots of unity e^ , where ''k'' runs over the positive integers less than ''n'' and coprime to ''n'' (and ''i'' is the imaginary unit). In other words, the ''n''th cyclotomic polynomial is equal to : \Phi_n(x) = \prod_\stackrel \left(x-e^\right). It may also be defined as the monic polynomial with integer coefficients that is the minimal polynomial over the field of the rational numbers of any primitive ''n''th-root of unity ( e^ is an example of such a root). An important relation linking cyclotomic polynomials and primitive roots of unity is :\prod_\Phi_d(x) = x^n - 1, showing that x is a root of x^n - 1 if and only if it is a ''d''th primitive root of unity for some ''d'' that divides ''n''. Examples If ''n'' is a prim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Factorization
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |