|
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
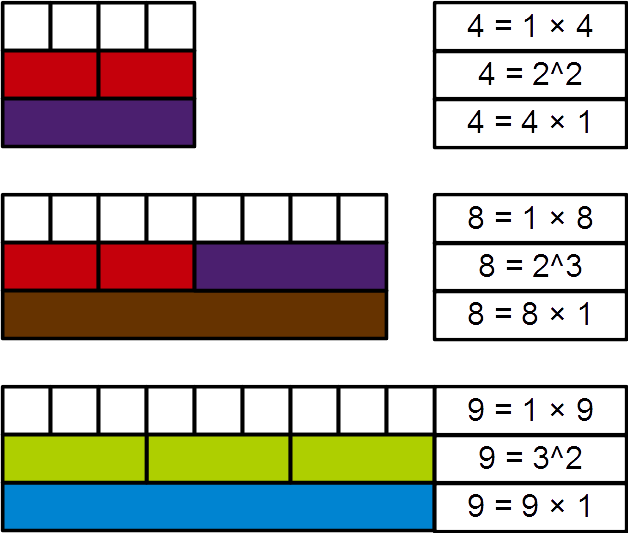
Perfect Power Number Cuisenaire Rods 9
Perfect commonly refers to: * Perfection, completeness, excellence * Perfect (grammar), a grammatical category in some languages Perfect may also refer to: Film * ''Perfect'' (1985 film), a romantic drama * ''Perfect'' (2018 film), a science fiction thriller Literature * ''Perfect'' (Friend novel), a 2004 novel by Natasha Friend * ''Perfect'' (Hopkins novel), a young adult novel by Ellen Hopkins * ''Perfect'' (Joyce novel), a 2013 novel by Rachel Joyce * ''Perfect'' (Shepard novel), a Pretty Little Liars novel by Sara Shepard * ''Perfect'', a young adult science fiction novel by Dyan Sheldon Music * Perfect interval, in music theory * Perfect Records, a record label Artists * Perfect (musician) (born 1980), reggae singer * Perfect (Polish band) * Perfect (American band), an American alternative rock group Albums * ''Perfect'' (Intwine album) (2004) * ''Perfect'' (Half Japanese album) (2016) * ''perfecT'', an album by Sam Shaber * ''Perfect'', an album by True Fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goldbach–Euler Theorem
In mathematics, the Goldbach–Euler theorem (also known as Goldbach's theorem), states that the sum of 1/(''p'' − 1) over the set of perfect powers ''p'', excluding 1 and omitting repetitions, converges to 1: :\sum_^\frac= + \cdots = 1. This result was first published in Euler's 1737 paper "''Variæ observationes circa series infinitas''". Euler attributed the result to a letter (now lost) from Goldbach. Proof Goldbach's original proof to Euler involved assigning a constant to the harmonic series: \textstyle x = \sum_^\infty \frac, which is divergent. Such a proof is not considered rigorous by modern standards. There is a strong resemblance between the method of sieving out powers employed in his proof and the method of factorization used to derive Euler's product formula for the Riemann zeta function. Let x be given by :x = 1 + \frac + \frac + \frac + \frac + \frac + \frac + \frac \cdots Since the sum of the reciprocal of every power of two is \texts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Power
In mathematics, a prime power is a positive integer which is a positive integer power of a single prime number. For example: , and are prime powers, while , and are not. The sequence of prime powers begins: 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29, 31, 32, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 107, 109, 113, 121, 125, 127, 128, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 243, 251, … . The prime powers are those positive integers that are divisible by exactly one prime number; in particular, the number 1 is not a prime power. Prime powers are also called primary numbers, as in the primary decomposition. Properties Algebraic properties Prime powers are powers of prime numbers. Every prime power (except powers of 2) has a primitive root; thus the multiplicative group of integers modulo ''p''''n'' (i.e. the group of units of the ring Z/''p''''n''Z) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan's Conjecture
Catalan's conjecture (or Mihăilescu's theorem) is a theorem in number theory that was Conjecture, conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu at Paderborn University. The integers 23 and 32 are two perfect powers (that is, powers of exponent higher than one) of natural numbers whose values (8 and 9, respectively) are consecutive. The theorem states that this is the ''only'' case of two consecutive perfect powers. That is to say, that History The history of the problem dates back at least to Gersonides, who proved a special case of the conjecture in 1343 where (''x'', ''y'') was restricted to be (2, 3) or (3, 2). The first significant progress after Catalan made his conjecture came in 1850 when Victor-Amédée Lebesgue dealt with the case ''b'' = 2. In 1976, Robert Tijdeman applied Baker's method in transcendental number theory, transcendence theory to establish a bound on a,b and used existing results bounding '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preda Mihăilescu
Preda V. Mihăilescu (born 23 May 1955) is a Romanian mathematician, best known for his proof of the 158-year-old Catalan's conjecture. Biography Born in Bucharest,Stewart 2013 he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving a PhD from ETH Zürich in 1997. His PhD thesis, titled ''Cyclotomy of rings and primality testing'', was written under the direction of Erwin Engeler and Hendrik Lenstra. For several years, he did research at the University of Paderborn, Germany. Since 2005, he has held a professorship at the University of Göttingen. Major research In 2002, Mihăilescu proved Catalan's conjecture.Bilu et al. 2014. This number-theoretical conjecture, formulated by the French and Belgian mathematician Eugène Charles Catalan in 1844, had stood unresolved for 158 years. Mihăilescu's proof appeared in ''Crelle's Journal ''Crelle's Journal'', or just ''Crel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Common Divisor
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers ''x'', ''y'', the greatest common divisor of ''x'' and ''y'' is denoted \gcd (x,y). For example, the GCD of 8 and 12 is 4, that is, \gcd (8, 12) = 4. In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the word "divisor" may be replaced by "factor", so that other names include highest common factor (hcf), etc. Historically, other names for the same concept have included greatest common measure. This notion can be extended to polynomials (see Polynomial greatest common divisor) and other commutative rings (see below). Overview Definition The ''greatest common divisor'' (GCD) of two nonzero integers and is the greatest positive integer such that is a divisor of both and ; that is, there are integers and such that and , and is the largest s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Element
In mathematics, especially in order theory, a maximal element of a subset ''S'' of some preordered set is an element of ''S'' that is not smaller than any other element in ''S''. A minimal element of a subset ''S'' of some preordered set is defined dually as an element of ''S'' that is not greater than any other element in ''S''. The notions of maximal and minimal elements are weaker than those of greatest element and least element which are also known, respectively, as maximum and minimum. The maximum of a subset S of a preordered set is an element of S which is greater than or equal to any other element of S, and the minimum of S is again defined dually. In the particular case of a partially ordered set, while there can be at most one maximum and at most one minimum there may be multiple maximal or minimal elements. Specializing further to totally ordered sets, the notions of maximal element and maximum coincide, and the notions of minimal element and minimum coincide. As an exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, or the unit 1, so the composite numbers are exactly the numbers that are not prime and not a unit. For example, the integer 14 is a composite number because it is the product of the two smaller integers 2 × 7. Likewise, the integers 2 and 3 are not composite numbers because each of them can only be divided by one and itself. The composite numbers up to 150 are: :4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Definition An integer is divisible by a nonzero integer if there exists an integer such that n=km. This is written as :m\mid n. Other ways of saying the same thing are that divides , is a divisor of , is a factor of , and is a multiple of . If does not divide , then the notation is m\not\mid n. Usually, is required to be nonzero, but is allowed to be zero. With this convention, m \mid 0 for every nonzero integer . Some definitions omit the requirement that m be nonzero. General Divisors can be negative as well as positive, although sometimes the term is restricted to positive divisors. For example, there are six divisors of 4; they ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). One of the roles of computationa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
