|
Random Fields
In physics and mathematics, a random field is a random function over an arbitrary domain (usually a multi-dimensional space such as \mathbb^n). That is, it is a function f(x) that takes on a random value at each point x \in \mathbb^n(or some other domain). It is also sometimes thought of as a synonym for a stochastic process with some restriction on its index set. That is, by modern definitions, a random field is a generalization of a stochastic process where the underlying parameter need no longer be real or integer valued "time" but can instead take values that are multidimensional vectors or points on some manifold. Formal definition Given a probability space (\Omega, \mathcal, P), an ''X''-valued random field is a collection of ''X''-valued random variables indexed by elements in a topological space ''T''. That is, a random field ''F'' is a collection : \ where each F_t is an ''X''-valued random variable. Examples In its discrete version, a random field is a list of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Random Field
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is a generalization of the canonical ensemble to infinite systems. The canonical ensemble gives the probability of the system ''X'' being in state ''x'' (equivalently, of the random variable ''X'' having value ''x'') as :P(X=x) = \frac \exp ( - \beta E(x)). Here, is a function from the space of states to the real numbers; in physics applications, is interpreted as the energy of the configuration ''x''. The parameter is a free parameter; in physics, it is the inverse temperature. The normalizing constant is the partition function. However, in infinite systems, the total energy is no longer a finite number and cannot be used in the traditional construction of the probability distribution of a canonical ensemble. Traditional approaches in statistical physics studied the limit of intensive properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Magnetic Resonance Imaging
Functional magnetic resonance imaging or functional MRI (fMRI) measures brain activity by detecting changes associated with blood flow. This technique relies on the fact that cerebral blood flow and neuronal activation are coupled. When an area of the brain is in use, blood flow to that region also increases. The primary form of fMRI uses the blood-oxygen-level dependent (BOLD) contrast, discovered by Seiji Ogawa in 1990. This is a type of specialized brain and body scan used to map neural activity in the brain or spinal cord of humans or other animals by imaging the change in blood flow ( hemodynamic response) related to energy use by brain cells. Since the early 1990s, fMRI has come to dominate brain mapping research because it does not involve the use of injections, surgery, the ingestion of substances, or exposure to ionizing radiation. This measure is frequently corrupted by noise from various sources; hence, statistical procedures are used to extract the underlying sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
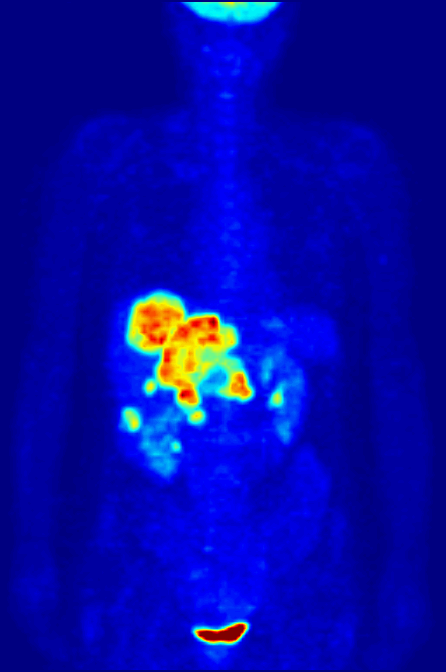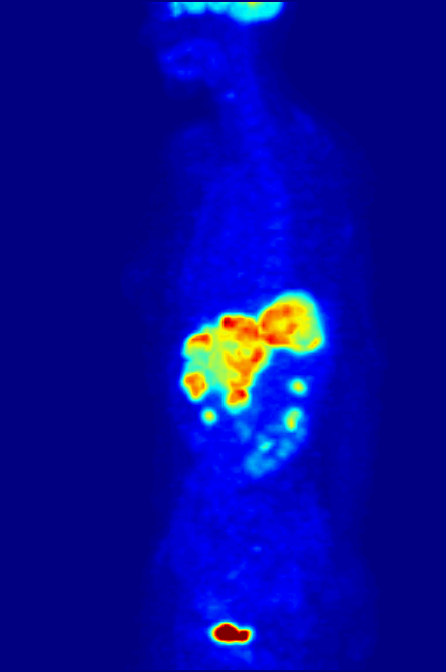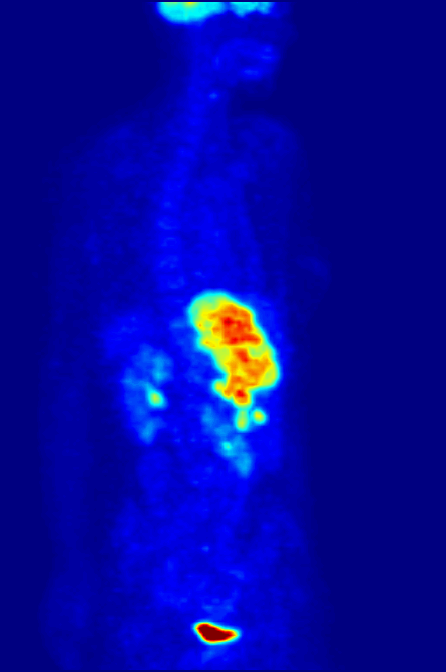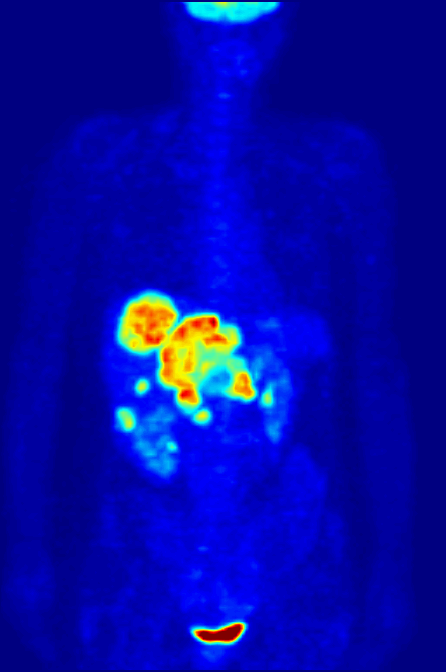
Positron Emission Tomography
Positron emission tomography (PET) is a functional imaging technique that uses radioactive substances known as radiotracers to visualize and measure changes in metabolic processes, and in other physiological activities including blood flow, regional chemical composition, and absorption. Different tracers are used for various imaging purposes, depending on the target process within the body. For example: * Fluorodeoxyglucose ( 18F">sup>18FDG or FDG) is commonly used to detect cancer; * 18Fodium fluoride">sup>18Fodium fluoride (Na18F) is widely used for detecting bone formation; * Oxygen-15 (15O) is sometimes used to measure blood flow. PET is a common imaging technique, a medical scintillography technique used in nuclear medicine. A radiopharmaceutical – a radioisotope attached to a drug – is injected into the body as a radioactive tracer, tracer. When the radiopharmaceutical undergoes beta plus decay, a positron is emitted, and when the positron interacts with an or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Neuroimaging
Functional neuroimaging is the use of neuroimaging technology to measure an aspect of brain function, often with a view to understanding the relationship between activity in certain brain areas and specific mental functions. It is primarily used as a research tool in cognitive neuroscience, cognitive psychology, neuropsychology, and social neuroscience. Overview Common methods of functional neuroimaging include * Positron emission tomography (PET) * Functional magnetic resonance imaging (fMRI) * Electroencephalography (EEG) * Magnetoencephalography (MEG) * Functional near-infrared spectroscopy (fNIRS) * Single-photon emission computed tomography (SPECT) * Functional ultrasound imaging (fUS) PET, fMRI, fNIRS and fUS can measure localized changes in cerebral blood flow related to neural activity. These changes are referred to as ''activations''. Regions of the brain which are activated when a subject performs a particular task may play a role in the neural computations which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neuroscience
Neuroscience is the science, scientific study of the nervous system (the brain, spinal cord, and peripheral nervous system), its functions and disorders. It is a Multidisciplinary approach, multidisciplinary science that combines physiology, anatomy, molecular biology, developmental biology, cytology, psychology, physics, computer science, chemistry, medicine, statistics, and Mathematical Modeling, mathematical modeling to understand the fundamental and emergent properties of neurons, glia and neural circuits. The understanding of the biological basis of learning, memory, behavior, perception, and consciousness has been described by Eric Kandel as the "epic challenge" of the Biology, biological sciences. The scope of neuroscience has broadened over time to include different approaches used to study the nervous system at different scales. The techniques used by neuroscientists have expanded enormously, from molecular biology, molecular and cell biology, cellular studies of indivi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Terrain Model
A digital elevation model (DEM) or digital surface model (DSM) is a 3D computer graphics representation of elevation data to represent terrain or overlaying objects, commonly of a planet, moon, or asteroid. A "global DEM" refers to a discrete global grid. DEMs are used often in geographic information systems (GIS), and are the most common basis for digitally produced relief maps. A digital terrain model (DTM) represents specifically the ground surface while DEM and DSM may represent tree top canopy or building roofs. While a DSM may be useful for landscape modeling, city modeling and visualization applications, a DTM is often required for flood or drainage modeling, land-use studies, geological applications, and other applications, and in planetary science. Terminology There is no universal usage of the terms ''digital elevation model'' (DEM), ''digital terrain model'' (DTM) and ''digital surface model'' (DSM) in scientific literature. In most cases the term ''digital s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Simulation
Fluid animation refers to computer graphics techniques for generating realistic animations of fluids such as water and smoke. Fluid animations are typically focused on emulating the qualitative visual behavior of a fluid, with less emphasis placed on rigorously correct physical results, although they often still rely on approximate solutions to the Euler equations or Navier–Stokes equations that govern real fluid physics. Fluid animation can be performed with different levels of complexity, ranging from time-consuming, high-quality animations for films, or visual effects, to simple and fast animations for real-time animations like computer games. Relationship to computational fluid dynamics Fluid animation differs from computational fluid dynamics (CFD) in that fluid animation is used primarily for visual effects, whereas computational fluid dynamics is used to study the behavior of fluids in a scientifically rigorous way. Development The development of fluid animati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ising Model
The Ising model () (or Lenz-Ising model or Ising-Lenz model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states (+1 or −1). The spins are arranged in a graph, usually a lattice (where the local structure repeats periodically in all directions), allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition. The Ising model was invented by the physicist , who gave it as a pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Sciences
Natural science is one of the branches of science concerned with the description, understanding and prediction of natural phenomena, based on empirical evidence from observation and experimentation. Mechanisms such as peer review and repeatability of findings are used to try to ensure the validity of scientific advances. Natural science can be divided into two main branches: life science and physical science. Life science is alternatively known as biology, and physical science is subdivided into branches: physics, chemistry, earth science, and astronomy. These branches of natural science may be further divided into more specialized branches (also known as fields). As empirical sciences, natural sciences use tools from the formal sciences, such as mathematics and logic, converting information about nature into measurements which can be explained as clear statements of the " laws of nature". Modern natural science succeeded more classical approaches to natural philosop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov assumption is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (conditional on both past and present values) depends only upon the pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |