Ising model

The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states (+1 or −1). The spins are arranged in a graph, usually a lattice (where the local structure repeats periodically in all directions), allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases.The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition. Though it is a highly simplified model of a magnetic material, the Ising model can still provide qualitative and sometimes quantitative results applicable to real physical systems.

The Ising model was invented by the physicist , who gave it as a problem to his student Ernst Ising. The one-dimensional Ising model was solved by alone in his 1924 thesis; it has no phase transition. The two-dimensional square-lattice Ising model is much harder and was only given an analytic description much later, by . It is usually solved by a transfer-matrix method, although there exists a very simple approach relating the model to a non-interacting fermionic quantum field theory.

In dimensions greater than four, the phase transition of the Ising model is described by mean-field theory. The Ising model for greater dimensions was also explored with respect to various tree topologies in the late 1970s, culminating in an exact solution of the zero-field, time-independent model for closed Cayley trees of arbitrary branching ratio, and thereby, arbitrarily large dimensionality within tree branches. The solution to this model exhibited a new, unusual phase transition behavior, along with non-vanishing long-range and nearest-neighbor spin-spin correlations, deemed relevant to large neural networks as one of its possible .

The Ising problem without an external field can be equivalently formulated as a graph maximum cut (Max-Cut) problem that can be solved via combinatorial optimization.

Definition

Consider a set $\Lambda$ of lattice sites, each with a set of adjacent sites (e.g. a graph) forming a $d$-dimensional lattice. For each lattice site $k\in\Lambda$ there is a discrete variable $\sigma_k$ such that $\sigma_k\in\$, representing the site's spin. A ''spin configuration'', $= \_$ is an assignment of spin value to each lattice site.

For any two adjacent sites $i, j\in\Lambda$ there is an ''interaction'' $J_$. Also a site $j\in\Lambda$ has an ''external magnetic field'' $h_j$ interacting with it. The ''energy'' of a configuration $$ is given by the Hamiltonian function

$H(\sigma) = -\sum_ J_ \sigma_i \sigma_j - \mu \sum_j h_j \sigma_j,$

where the first sum is over pairs of adjacent spins (every pair is counted once). The notation $\langle ij\rangle$ indicates that sites $i$ and $j$ are nearest neighbors. The magnetic moment is given by $\mu$. Note that the sign in the second term of the Hamiltonian above should actually be positive because the electron's magnetic moment is antiparallel to its spin, but the negative term is used conventionally. The Ising Hamiltonian is an example of a pseudo-Boolean function; tools from the analysis of Boolean functions can be applied to describe and study it.

The ''configuration probability'' is given by the Boltzmann distribution with inverse temperature $\beta\geq0$:

$P_\beta(\sigma) = \frac,$

where $\beta = 1 / (k_\text T)$, and the normalization constant

$Z_\beta = \sum_\sigma e^$

is the partition function. For a function $f$ of the spins ("observable"), one denotes by

$\langle f \rangle_\beta = \sum_\sigma f(\sigma) P_\beta(\sigma)$

the expectation (mean) value of $f$.

The configuration probabilities $P_(\sigma)$ represent the probability that (in equilibrium) the system is in a state with configuration $\sigma$.

Discussion

The minus sign on each term of the Hamiltonian function $H(\sigma)$ is conventional. Using this sign convention, Ising models can be classified according to the sign of the interaction: if, for a pair ''i'', ''j''

The system is called ferromagnetic or antiferromagnetic if all interactions are ferromagnetic or all are antiferromagnetic. The original Ising models were ferromagnetic, and it is still often assumed that "Ising model" means a ferromagnetic Ising model.

In a ferromagnetic Ising model, spins desire to be aligned: the configurations in which adjacent spins are of the same sign have higher probability. In an antiferromagnetic model, adjacent spins tend to have opposite signs.

The sign convention of ''H''(σ) also explains how a spin site ''j'' interacts with the external field. Namely, the spin site wants to line up with the external field. If:

Simplifications

Ising models are often examined without an external field interacting with the lattice, that is, ''h'' = 0 for all ''j'' in the lattice Λ. Using this simplification, the Hamiltonian becomes

$H(\sigma) = -\sum_ J_ \sigma_i \sigma_j.$

When the external field is zero everywhere, ''h'' = 0, the Ising model is symmetric under switching the value of the spin in all the lattice sites; a nonzero field breaks this symmetry.

Another common simplification is to assume that all of the nearest neighbors ⟨''ij''⟩ have the same interaction strength. Then we can set ''J_ij'' = ''J'' for all pairs ''i'', ''j'' in Λ. In this case the Hamiltonian is further simplified to

$H(\sigma) = -J \sum_ \sigma_i \sigma_j.$

Connection to

graph maximum cut

A subset S of the vertex set V(G) of a weighted undirected graph G determines a cut of the graph G into S and its complementary subset G\S. The size of the cut is the sum of the weights of the edges between S and G\S. A maximum cut size is at least the size of any other cut, varying S.

For the Ising model without an external field on a graph G, the Hamiltonian becomes the following sum over the graph edges E(G)

:$H(\sigma) = -\sum_ J_\sigma_i\sigma_j$.

Here each vertex i of the graph is a spin site that takes a spin value $\sigma_i = \pm 1$. A given spin configuration $\sigma$ partitions the set of vertices $V(G)$ into two $\sigma$-depended subsets, those with spin up $V^+$ and those with spin down $V^-$. We denote by $\delta(V^+)$ the $\sigma$-depended set of edges that connects the two complementary vertex subsets $V^+$ and $V^-$. The ''size'' $\left, \delta(V^+)\$ of the cut $\delta(V^+)$ to bipartite the weighted undirected graph G can be defined as

$\left, \delta(V^+)\=\frac12\sum_ W_,$

where $W_$ denotes a weight of the edge $ij$ and the scaling 1/2 is introduced to compensate for double counting the same weights $W_=W_$.

The identities

$\begin H(\sigma) &= -\sum_ J_ - \sum_ J_ + \sum_ J_ \\ &= - \sum_ J_ + 2 \sum_ J_, \end$

where the total sum in the first term does not depend on $\sigma$, imply that minimizing $H(\sigma)$ in $\sigma$ is equivalent to minimizing $\sum_ J_$. Defining the edge weight $W_=-J_$ thus turns the Ising problem without an external field into a graph Max-Cut problem
maximizing the cut size $\left, \delta(V^+)\$, which is related to the Ising Hamiltonian as follows,

$H(\sigma) = \sum_ W_ - 4 \left, \delta(V^+)\.$

Questions

A significant number of statistical questions to ask about this model are in the limit of large numbers of spins:
* In a typical configuration, are most of the spins +1 or −1, or are they split equally?
* If a spin at any given position ''i'' is 1, what is the probability that the spin at position ''j'' is also 1?
* If ''β'' is changed, is there a phase transition?
* On a lattice Λ, what is the fractal dimension of the shape of a large cluster of +1 spins?

Basic properties and history

The most studied case of the Ising model is the translation-invariant ferromagnetic zero-field model on a ''d''-dimensional lattice, namely, Λ = Z^''d'', ''J''_''ij'' = 1, ''h'' = 0.

No phase transition in one dimension

In his 1924 PhD thesis, Ising solved the model for the ''d'' = 1 case, which can be thought of as a linear horizontal lattice where each site only interacts with its left and right neighbor. In one dimension, the solution admits no phase transition. Namely, for any positive β, the correlations ⟨σ_''i''σ_''j''⟩ decay exponentially in , ''i'' − ''j'', :
$\langle \sigma_i \sigma_j \rangle_\beta \leq C \exp\left(-c(\beta) , i - j, \right),$

and the system is disordered. On the basis of this result, he incorrectly concluded that this model does not exhibit phase behaviour in any dimension.

Phase transition and exact solution in two dimensions

The Ising model undergoes a phase transition between an ordered and a disordered phase in 2 dimensions or more. Namely, the system is disordered for small β, whereas for large β the system exhibits ferromagnetic order:

$\langle \sigma_i \sigma_j \rangle_\beta \geq c(\beta) > 0.$

This was first proven by Rudolf Peierls in 1936, using what is now called a Peierls argument.

The Ising model on a two-dimensional square lattice with no magnetic field was analytically solved by . Onsager obtained the correlation functions and free energy of the Ising model and announced the formula for the spontaneous magnetization for the 2-dimensional model in 1949 but did not give a derivation. gave the first published proof of this formula, using a limit formula for Fredholm determinants, proved in 1951 by Szegő in direct response to Onsager's work.

Correlation inequalities

A number of correlation inequalities have been derived rigorously for the Ising spin correlations (for general lattice structures), which have enabled mathematicians to study the Ising model both on and off criticality.

Griffiths inequality

Given any subset of spins $\sigma_A$ and $\sigma_B$ on the lattice, the following inequality holds,

$\langle \sigma_A \sigma_B \rangle \geq \langle \sigma_A \rangle \langle \sigma_B \rangle,$

where $\langle \sigma_A \rangle = \langle \prod_ \sigma_j \rangle$.

With $B = \empty$, the special case $\langle \sigma_A \rangle \ge 0$ results.

This means that spins are positively correlated on the Ising ferromagnet. An immediate application of this is that the magnetization of any set of spins $\langle \sigma_A \rangle$ is increasing with respect to any set of coupling constants $J_B$.

Simon-Lieb inequality

The Simon-Lieb inequality states that for any set $S$ disconnecting $x$ from $y$ (e.g. the boundary of a box with $x$ being inside the box and $y$ being outside),

$\langle \sigma_x \sigma_y \rangle \leq \sum_ \langle \sigma_x \sigma_z \rangle \langle \sigma_z \sigma_y \rangle.$

This inequality can be used to establish the sharpness of phase transition for the Ising model.

FKG inequality

This inequality is proven first for a type of positively-correlated percolation model, of which includes a representation of the Ising model. It is used to determine the critical temperatures of planar Potts model using percolation arguments (which includes the Ising model as a special case).

Historical significance

While the laws of chemical bonding made it clear to nineteenth century chemists that atoms were real, among physicists the debate continued well into the early twentieth century. Atomists, notably James Clerk Maxwell and Ludwig Boltzmann, applied Hamilton's formulation of Newton's laws to large systems, and found that the statistical behavior of the atoms correctly describes room temperature gases. But classical statistical mechanics did not account for all of the properties of liquids and solids, nor of gases at low temperature.

Once modern quantum mechanics was formulated, atomism was no longer in conflict with experiment, but this did not lead to a universal acceptance of statistical mechanics, which went beyond atomism. Josiah Willard Gibbs had given a complete formalism to reproduce the laws of thermodynamics from the laws of mechanics. But many faulty arguments survived from the 19th century, when statistical mechanics was considered dubious. The lapses in intuition mostly stemmed from the fact that the limit of an infinite statistical system has many zero-one laws which are absent in finite systems: an infinitesimal change in a parameter can lead to big differences in the overall, aggregate behavior.

No phase transitions in finite volume

In the early part of the twentieth century, some believed that the partition function could never describe a phase transition, based on the following argument:

# The partition function is a sum of ''e''^−β''E'' over all configurations.
# The exponential function is everywhere analytic as a function of β.
# The sum of analytic functions is an analytic function.

This argument works for a finite sum of exponentials, and correctly establishes that there are no singularities in the free energy of a system of a finite size. For systems which are in the thermodynamic limit (that is, for infinite systems) the infinite sum can lead to singularities. The convergence to the thermodynamic limit is fast, so that the phase behavior is apparent already on a relatively small lattice, even though the singularities are smoothed out by the system's finite size.

This was first established by Rudolf Peierls in the Ising model.

Peierls droplets

Shortly after Lenz and Ising constructed the Ising model, Peierls was able to explicitly show that a phase transition occurs in two dimensions.

To do this, he compared the high-temperature and low-temperature limits. At infinite temperature (β = 0) all configurations have equal probability. Each spin is completely independent of any other, and if typical configurations at infinite temperature are plotted so that plus/minus are represented by black and white, they look like television snow. For high, but not infinite temperature, there are small correlations between neighboring positions, the snow tends to clump a little bit, but the screen stays randomly looking, and there is no net excess of black or white.

A quantitative measure of the excess is the magnetization, which is the average value of the spin:

$M = \frac \sum_^N \sigma_i.$

A bogus argument analogous to the argument in the last section now establishes that the ''average'' magnetization in the Ising model is always zero.
# Every configuration of spins has equal energy to the configuration with all spins flipped.
# So for every configuration with magnetization ''M'' there is a configuration with magnetization −''M'' with equal probability.
# The system should therefore spend equal amounts of time in the configuration with magnetization ''M'' as with magnetization −''M''.
# So the average magnetization (over all time) is zero.

As before, this only proves that the average magnetization is zero at any finite volume. For an infinite system, fluctuations might not be able to push the system from a mostly plus state to a mostly minus with a nonzero probability.

For very high temperatures, the magnetization is zero, as it is at infinite temperature. To see this, note that if spin A has only a small correlation ε with spin B, and B is only weakly correlated with C, but C is otherwise independent of A, the amount of correlation of A and C goes like ε². For two spins separated by distance ''L'', the amount of correlation goes as ε^''L'', but if there is more than one path by which the correlations can travel, this amount is enhanced by the number of paths.

The number of paths of length ''L'' on a square lattice in ''d'' dimensions is
$N(L) = (2d)^L,$
since there are 2''d'' choices for where to go at each step.

A bound on the total correlation is given by the contribution to the correlation by summing over all paths linking two points, which is bounded above by the sum over all paths of length ''L'' divided by
$\sum_L (2d)^L \varepsilon^L,$
which goes to zero when ε is small.

At low temperatures (β ≫ 1) the configurations are near the lowest-energy configuration, the one where all the spins are plus or all the spins are minus. Peierls asked whether it is statistically possible at low temperature, starting with all the spins minus, to fluctuate to a state where most of the spins are plus. For this to happen, droplets of plus spin must be able to congeal to make the plus state.

The energy of a droplet of plus spins in a minus background is proportional to the perimeter of the droplet L, where plus spins and minus spins neighbor each other. For a droplet with perimeter ''L'', the area is somewhere between (''L'' − 2)/2 (the straight line) and (''L''/4)² (the square box). The probability cost for introducing a droplet has the factor ''e''^−β''L'', but this contributes to the partition function multiplied by the total number of droplets with perimeter ''L'', which is less than the total number of paths of length ''L'':
$N(L) < 4^.$
So that the total spin contribution from droplets, even overcounting by allowing each site to have a separate droplet, is bounded above by
$\sum_L L^2 4^ e^,$

which goes to zero at large β. For β sufficiently large, this exponentially suppresses long loops, so that they cannot occur, and the magnetization never fluctuates too far from −1.

So Peierls established that the magnetization in the Ising model eventually defines superselection sectors, separated domains not linked by finite fluctuations.

Kramers–Wannier duality

Kramers and Wannier were able to show that the high-temperature expansion and the low-temperature expansion of the model are equal up to an overall rescaling of the free energy. This allowed the phase-transition point in the two-dimensional model to be determined exactly (under the assumption that there is a unique critical point).

Yang–Lee zeros

After Onsager's solution, Yang and Lee investigated the way in which the partition function becomes singular as the temperature approaches the critical temperature.

Applications

Magnetism

The original motivation for the model was the phenomenon of ferromagnetism. Iron is magnetic; once it is magnetized it stays magnetized for a long time compared to any atomic time.

In the 19th century, it was thought that magnetic fields are due to currents in matter, and Ampère postulated that permanent magnets are caused by permanent atomic currents. The motion of classical charged particles could not explain permanent currents though, as shown by Larmor. In order to have ferromagnetism, the atoms must have permanent magnetic moments which are not due to the motion of classical charges.

Once the electron's spin was discovered, it was clear that the magnetism should be due to a large number of electron spins all oriented in the same direction. It was natural to ask how the electrons' spins all know which direction to point in, because the electrons on one side of a magnet don't directly interact with the electrons on the other side. They can only influence their neighbors. The Ising model was designed to investigate whether a large fraction of the electron spins could be oriented in the same direction using only local forces.

Lattice gas

The Ising model can be reinterpreted as a statistical model for the motion of atoms. Since the kinetic energy depends only on momentum and not on position, while the statistics of the positions only depends on the potential energy, the thermodynamics of the gas only depends on the potential energy for each configuration of atoms.

A coarse model is to make space-time a lattice and imagine that each position either contains an atom or it doesn't. The space of configuration is that of independent bits ''B_i'', where each bit is either 0 or 1 depending on whether the position is occupied or not. An attractive interaction reduces the energy of two nearby atoms. If the attraction is only between nearest neighbors, the energy is reduced by −4''JB''_''i''''B''_''j'' for each occupied neighboring pair.

The density of the atoms can be controlled by adding a chemical potential, which is a multiplicative probability cost for adding one more atom. A multiplicative factor in probability can be reinterpreted as an additive term in the logarithm – the energy. The extra energy of a configuration with ''N'' atoms is changed by ''μN''. The probability cost of one more atom is a factor of exp(−''βμ'').

So the energy of the lattice gas is:
$E = - \frac \sum_ 4 J B_i B_j + \sum_i \mu B_i.$

Rewriting the bits in terms of spins, $B_i = (S_i + 1)/2.$
$E = - \frac \sum_ J S_i S_j - \frac \sum_i (4 J - \mu) S_i.$

For lattices where every site has an equal number of neighbors, this is the Ising model with a magnetic field ''h'' = (''zJ'' − ''μ'')/2, where ''z'' is the number of neighbors.

In biological systems, modified versions of the lattice gas model have been used to understand a range of binding behaviors. These include the binding of ligands to receptors in the cell surface, the binding of chemotaxis proteins to the flagellar motor, and the condensation of DNA.

Neuroscience

The activity of neurons in the brain can be modelled statistically. Each neuron at any time is either active + or inactive −. The active neurons are those that send an action potential down the axon in any given time window, and the inactive ones are those that do not.

Following the general approach of Jaynes, a later interpretation of Schneidman, Berry, Segev and Bialek,
is that the Ising model is useful for any model of neural function, because a statistical model for neural activity should be chosen using the principle of maximum entropy. Given a collection of neurons, a statistical model which can reproduce the average firing rate for each neuron introduces a Lagrange multiplier for each neuron:
$E = - \sum_i h_i S_i$
But the activity of each neuron in this model is statistically independent. To allow for pair correlations, when one neuron tends to fire (or not to fire) along with another, introduce pair-wise lagrange multipliers:
$E= - \tfrac \sum_ J_ S_i S_j - \sum_i h_i S_i$
where $J_$ are not restricted to neighbors. Note that this generalization of Ising model is sometimes called the quadratic exponential binary distribution in statistics.
This energy function only introduces probability biases for a spin having a value and for a pair of spins having the same value. Higher order correlations are unconstrained by the multipliers. An activity pattern sampled from this distribution requires the largest number of bits to store in a computer, in the most efficient coding scheme imaginable, as compared with any other distribution with the same average activity and pairwise correlations. This means that Ising models are relevant to any system which is described by bits which are as random as possible, with constraints on the pairwise correlations and the average number of 1s, which frequently occurs in both the physical and social sciences.

Spin glasses

With the Ising model the so-called spin glasses can also be described, by the usual Hamiltonian $H=-\frac\,\sum J_\,S_i\,S_k,$ where the ''S''-variables describe the Ising spins, while the ''J_i,k'' are taken from a random distribution. For spin glasses a typical distribution chooses antiferromagnetic bonds with probability ''p'' and ferromagnetic bonds with probability 1 − ''p'' (also known as the random-bond Ising model). These bonds stay fixed or "quenched" even in the presence of thermal fluctuations. When ''p'' = 0 we have the original Ising model. This system deserves interest in its own; particularly one has "non-ergodic" properties leading to strange relaxation behaviour. Much attention has been also attracted by the related bond and site dilute Ising model, especially in two dimensions, leading to intriguing critical behavior.

Artificial neural network

Ising model was instrumental in the development of the Hopfield network. The original Ising model is a model for equilibrium. Roy J. Glauber in 1963 studied the Ising model evolving in time, as a process towards thermal equilibrium ( Glauber dynamics), adding in the component of time. (Kaoru Nakano, 1971) and ( Shun'ichi Amari, 1972), proposed to modify the weights of an Ising model by Hebbian learning rule as a model of associative memory. The same idea was published by (, 1974), who was cited by Hopfield in his 1982 paper.

The Sherrington–Kirkpatrick model of spin glass, published in 1975, is the Hopfield network with random initialization. Sherrington and Kirkpatrick found that it is highly likely for the energy function of the SK model to have many local minima. In the 1982 paper, Hopfield applied this recently developed theory to study the Hopfield network with binary activation functions. In a 1984 paper he extended this to continuous activation functions. It became a standard model for the study of neural networks through statistical mechanics.

Sea ice

The melt pond can be modelled by the Ising model; sea ice topography data bears rather heavily on the results. The state variable is binary for a simple 2D approximation, being either water or ice.

Cayley tree topologies and large neural networks

In order to investigate an Ising model with potential relevance for large (e.g. with $10^4$ or $10^5$ interactions per node) neural nets, at the suggestion of Krizan in 1979, obtained the exact analytical expression for the free energy of the Ising model on the closed Cayley tree (with an arbitrarily large branching ratio) for a zero-external magnetic field (in the thermodynamic limit) by applying the methodologies of and

$-\beta f = \ln 2 + \frac \ln (\cosh J) + \frac \sum_^z\frac\ln J_i (\tau)$

where $\gamma$ is an arbitrary branching ratio (greater than or equal to 2), $t \equiv \tanh J$, $\tau \equiv t^2$, $J \equiv \beta\epsilon$ (with $\epsilon$ representing the nearest-neighbor interaction energy) and there are k (→ ∞ in the thermodynamic limit) generations in each of the tree branches (forming the closed tree architecture as shown in the given closed Cayley tree diagram.) The sum in the last term can be shown to converge uniformly and rapidly (i.e. for z → ∞, it remains finite) yielding a continuous and monotonous function, establishing that, for $\gamma$ greater than or equal to 2, the free energy is a continuous function of temperature T. Further analysis of the free energy indicates that it exhibits an unusual discontinuous first derivative at the critical temperature (, .)

The spin-spin correlation between sites (in general, m and n) on the tree was found to have a transition point when considered at the vertices (e.g. A and Ā, its reflection), their respective neighboring sites (such as B and its reflection), and between sites adjacent to the top and bottom extreme vertices of the two trees (e.g. A and B), as may be determined from
\langle s_m s_n \rangle = ^(0,T) cosh J 2^N \sum_^z g_(l) t^l
where $N_b$ is equal to the number of bonds, $g_(l)t^l$ is the number of graphs counted for odd vertices with even intermediate sites (see cited methodologies and references for detailed calculations), $2^N$ is the multiplicity resulting from two-valued spin possibilities and the partition function $$ is derived from $\sum_e^$. (Note: $s_i$ is consistent with the referenced literature in this section and is equivalent to $S_i$ or $\sigma_i$ utilized above and in earlier sections; it is valued at $\pm 1$.) The critical temperature $T_C$ is given by
$T_C = \frac.$

The critical temperature for this model is only determined by the branching ratio $\gamma$ and the site-to-site interaction energy $\epsilon$, a fact which may have direct implications associated with neural structure vs. its function (in that it relates the energies of interaction and branching ratio to its transitional behavior.) For example, a relationship between the transition behavior of activities of neural networks between sleeping and wakeful states (which may correlate with a spin-spin type of phase transition) in terms of changes in neural interconnectivity ($\gamma$) and/or neighbor-to-neighbor interactions ($\epsilon$), over time, is just one possible avenue suggested for further experimental investigation into such a phenomenon. In any case, for this Ising model it was established, that “the stability of the long-range correlation increases with increasing $\gamma$ or increasing $\epsilon$.”

For this topology, the spin-spin correlation was found to be zero between the extreme vertices and the central sites at which the two trees (or branches) are joined (i.e. between A and individually C, D, or E.) This behavior is explained to be due to the fact that, as k increases, the number of links increases exponentially (between the extreme vertices) and so even though the contribution to spin correlations decrease exponentially, the correlation between sites such as the extreme vertex (A) in one tree and the extreme vertex in the joined tree (Ā) remains finite (above the critical temperature.) In addition, A and B also exhibit a non-vanishing correlation (as do their reflections) thus lending itself to, for B level sites (with A level), being considered “clusters” which tend to exhibit synchronization of firing.

Based upon a review of other classical network models as a comparison, the Ising model on a closed Cayley tree was determined to be the first classical statistical mechanical model to demonstrate both local and long-range sites with non-vanishing spin-spin correlations, while at the same time exhibiting intermediate sites with zero correlation, which indeed was a relevant matter for large neural networks at the time of its consideration. The model's behavior is also of relevance for any other divergent-convergent tree physical (or biological) system exhibiting a closed Cayley tree topology with an Ising-type of interaction. This topology should not be ignored since its behavior for Ising models has been solved exactly, and presumably nature will have found a way of taking advantage of such simple symmetries at many levels of its designs.

early on noted the possibility of interrelationships between (1) the classical large neural network model (with similar coupled divergent-convergent topologies) with (2) an underlying statistical quantum mechanical model (independent of topology and with persistence in fundamental quantum states):

It was a natural and common belief among early neurophysicists (e.g. Umezawa, Krizan, Barth, etc.) that classical neural models (including those with statistical mechanical aspects) will one day have to be integrated with quantum physics (with quantum statistical aspects), similar perhaps to how the domain of chemistry has historically integrated itself into quantum physics via quantum chemistry.

Several additional statistical mechanical problems of interest remain to be solved for the closed Cayley tree, including the time-dependent case and the external field situation, as well as theoretical efforts aimed at understanding interrelationships with underlying quantum constituents and their physics.

Numerical simulation

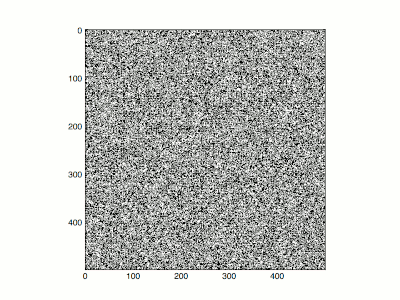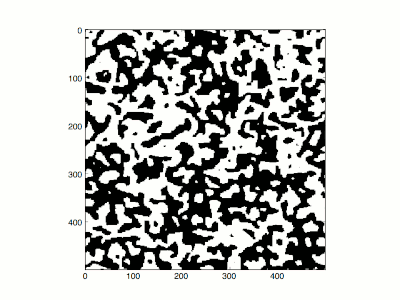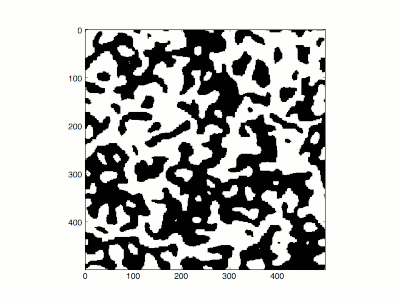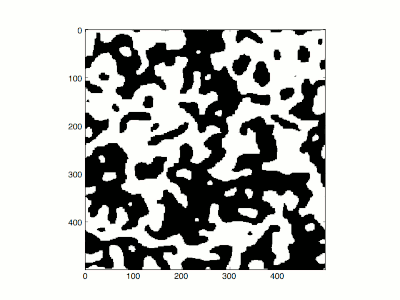
The Ising model can often be difficult to evaluate numerically if there are many states in the system. Consider an Ising model with
: ''L'' = , Λ, : the total number of sites on the lattice,
: σ_''j'' ∈ : an individual spin site on the lattice, ''j'' = 1, ..., ''L'',
: ''S'' ∈ ^''L'': state of the system.

Since every spin site has ±1 spin, there are ''2''^''L'' different states that are possible. This motivates the reason for the Ising model to be simulated using Monte Carlo methods.

The Hamiltonian that is commonly used to represent the energy of the model when using Monte Carlo methods is:

$H(\sigma) = -J \sum_ \sigma_i \sigma_j - h \sum_j \sigma_j.$

Furthermore, the Hamiltonian is further simplified by assuming zero external field ''h'', since many questions that are posed to be solved using the model can be answered in absence of an external field. This leads us to the following energy equation for state σ:

$H(\sigma) = -J \sum_ \sigma_i \sigma_j.$

Given this Hamiltonian, quantities of interest such as the specific heat or the magnetization of the magnet at a given temperature can be calculated.

Metropolis algorithm

The Metropolis–Hastings algorithm is the most commonly used Monte Carlo algorithm to calculate Ising model estimations. The algorithm first chooses ''selection probabilities'' ''g''(μ, ν), which represent the probability that state ν is selected by the algorithm out of all states, given that one is in state μ. It then uses acceptance probabilities ''A''(μ, ν) so that detailed balance is satisfied. If the new state ν is accepted, then we move to that state and repeat with selecting a new state and deciding to accept it. If ν is not accepted then we stay in μ. This process is repeated until some stopping criterion is met, which for the Ising model is often when the lattice becomes ferromagnetic, meaning all of the sites point in the same direction.

When implementing the algorithm, one must ensure that ''g''(μ, ν) is selected such that ergodicity is met. In thermal equilibrium a system's energy only fluctuates within a small range. This is the motivation behind the concept of single-spin-flip dynamics, which states that in each transition, we will only change one of the spin sites on the lattice. Furthermore, by using single- spin-flip dynamics, one can get from any state to any other state by flipping each site that differs between the two states one at a time. The maximum amount of change between the energy of the present state, ''H''_μ and any possible new state's energy ''H''_ν (using single-spin-flip dynamics) is 2''J'' between the spin we choose to "flip" to move to the new state and that spin's neighbor. Thus, in a 1D Ising model, where each site has two neighbors (left and right), the maximum difference in energy would be 4''J''. Let ''c'' represent the ''lattice coordination number''; the number of nearest neighbors that any lattice site has. We assume that all sites have the same number of neighbors due to periodic boundary conditions. It is important to note that the Metropolis–Hastings algorithm does not perform well around the critical point due to critical slowing down. Other techniques such as multigrid methods, Niedermayer's algorithm, Swendsen–Wang algorithm, or the Wolff algorithm are required in order to resolve the model near the critical point; a requirement for determining the critical exponents of the system.

Specifically for the Ising model and using single-spin-flip dynamics, one can establish the following. Since there are ''L'' total sites on the lattice, using single-spin-flip as the only way we transition to another state, we can see that there are a total of ''L'' new states ν from our present state μ. The algorithm assumes that the selection probabilities are equal to the ''L'' states: ''g''(μ, ν) = 1/''L''. Detailed balance tells us that the following equation must hold:

$\frac = \frac = \frac = \frac = \frac = e^.$

Thus, we want to select the acceptance probability for our algorithm to satisfy

$\frac = e^.$

If ''H''_ν > ''H''_μ, then ''A''(ν, μ) > ''A''(μ, ν). Metropolis sets the larger of ''A''(μ, ν) or ''A''(ν, μ) to be 1. By this reasoning the acceptance algorithm is:

$A(\mu, \nu) = \begin e^, & \text H_\nu - H_\mu > 0, \\ 1 & \text. \end$

The basic form of the algorithm is as follows:

# Pick a spin site using selection probability ''g''(μ, ν) and calculate the contribution to the energy involving this spin.
# Flip the value of the spin and calculate the new contribution.
# If the new energy is less, keep the flipped value.
# If the new energy is more, only keep with probability $e^.$
# Repeat.

The change in energy ''H''_ν − ''H''_μ only depends on the value of the spin and its nearest graph neighbors. So if the graph is not too connected, the algorithm is fast. This process will eventually produce a pick from the distribution.

As a Markov chain

It is possible to view the Ising model as a Markov chain, as the immediate probability ''P''_β(ν) of transitioning to a future state ν only depends on the present state μ. The Metropolis algorithm is actually a version of a Markov chain Monte Carlo simulation, and since we use single-spin-flip dynamics in the Metropolis algorithm, every state can be viewed as having links to exactly ''L'' other states, where each transition corresponds to flipping a single spin site to the opposite value. Furthermore, since the energy equation ''H''_σ change only depends on the nearest-neighbor interaction strength ''J'', the Ising model and its variants such the Sznajd model can be seen as a form of a voter model for opinion dynamics.

Solutions

One dimension

The thermodynamic limit exists as long as the interaction decay is $J_ \sim , i - j, ^$ with α > 1.

* In the case of ''ferromagnetic'' interaction $J_ \sim , i - j, ^$ with 1 < α < 2, Dyson proved, by comparison with the hierarchical case, that there is phase transition at small enough temperature.
* In the case of ''ferromagnetic'' interaction $J_ \sim , i - j, ^$, Fröhlich and Spencer proved that there is phase transition at small enough temperature (in contrast with the hierarchical case).
* In the case of interaction $J_ \sim , i - j, ^$ with α > 2 (which includes the case of finite-range interactions), there is no phase transition at any positive temperature (i.e. finite β), since the free energy is analytic in the thermodynamic parameters.
* In the case of ''nearest neighbor'' interactions, E. Ising provided an exact solution of the model. At any positive temperature (i.e. finite β) the free energy is analytic in the thermodynamics parameters, and the truncated two-point spin correlation decays exponentially fast. At zero temperature (i.e. infinite β), there is a second-order phase transition: the free energy is infinite, and the truncated two-point spin correlation does not decay (remains constant). Therefore, ''T'' = 0 is the critical temperature of this case. Scaling formulas are satisfied.

Ising's exact solution

In the nearest neighbor case (with periodic or free boundary conditions) an exact solution is available. The Hamiltonian of the one-dimensional Ising model on a lattice of ''L'' sites with free boundary conditions is
$H(\sigma) = -J \sum_ \sigma_i \sigma_ - h \sum_i \sigma_i,$
where ''J'' and ''h'' can be any number, since in this simplified case ''J'' is a constant representing the interaction strength between the nearest neighbors and ''h'' is the constant external magnetic field applied to lattice sites. Then the
free energy is
$f(\beta, h) = -\lim_ \frac \ln Z(\beta) = -\frac \ln\left(e^ \cosh \beta h + \sqrt\right),$
and the spin-spin correlation (i.e. the covariance) is
$\langle\sigma_i \sigma_j\rangle - \langle\sigma_i\rangle \langle\sigma_j\rangle = C(\beta) e^,$
where ''C''(β) and ''c''(β) are positive functions for ''T'' > 0. For ''T'' → 0, though, the inverse correlation length ''c''(β) vanishes.

= Proof

=

The proof of this result is a simple computation.

If ''h'' = 0, it is very easy to obtain the free energy in the case of free boundary condition, i.e. when
$H(\sigma) = -J \left(\sigma_1 \sigma_2 + \cdots + \sigma_ \sigma_L\right).$
Then the model factorizes under the change of variables
$\sigma'_j = \sigma_j \sigma_, \quad j \ge 2.$

This gives
Z(\beta) = \sum_ e^ e^ \cdots e^ = 2 \prod_^L \sum_ e^ = 2 \left ^ + e^\right.

Therefore, the free energy is

f(\beta, 0) = -\frac \ln\left ^ + e^\right

With the same change of variables

\langle\sigma_j\sigma_\rangle = \left frac\rightN,

hence it decays exponentially as soon as ''T'' ≠ 0; but for ''T'' = 0, i.e. in the limit β → ∞ there is no decay.

If ''h'' ≠ 0 we need the transfer matrix method. For the periodic boundary conditions case is the following. The partition function is
$Z(\beta) = \sum_ e^ e^ e^ e^ \cdots e^ e^ = \sum_ V_ V_ \cdots V_.$
The coefficients $V_$ can be seen as the entries of a matrix. There are different possible choices: a convenient one (because the matrix is symmetric) is
$V_ = e^ e^ e^$
or
$V = \begin e^ & e^ \\ e^ & e^ \end.$
In matrix formalism
Z(\beta) = \operatorname \left(V^L\right) = \lambda_1^L + \lambda_2^L = \lambda_1^L \left + \left(\frac\right)^L\right
where λ₁ is the highest eigenvalue of ''V'', while is the other eigenvalue:
$\lambda_1 = e^ \cosh \beta h + \sqrt=e^ \cosh \beta h + \sqrt,$
and . This gives the formula of the free energy above. In the thermodynamics limit for the non-interaction case (J = 0), we got
$Z_N \to (\lambda_1)^N = (2\cosh \beta h)^N,$
as the answer for the open-boundary Ising model.

= Comments

=

The energy of the lowest state is −''JL'', when all the spins are the same. For any other configuration, the extra energy is equal to 2''J'' times the number of sign changes that are encountered when scanning the configuration from left to right.

If we designate the number of sign changes in a configuration as ''k'', the difference in energy from the lowest energy state is 2''k''. Since the energy is additive in the number of flips, the probability ''p'' of having a spin-flip at each position is independent. The ratio of the probability of finding a flip to the probability of not finding one is the Boltzmann factor:

$\frac = e^.$

The problem is reduced to independent biased coin tosses. This essentially completes the mathematical description.

From the description in terms of independent tosses, the statistics of the model for long lines can be understood. The line splits into domains. Each domain is of average length exp(2β). The length of a domain is distributed exponentially, since there is a constant probability at any step of encountering a flip. The domains never become infinite, so a long system is never magnetized. Each step reduces the correlation between a spin and its neighbor by an amount proportional to ''p'', so the correlations fall off exponentially.

$\langle S_i S_j \rangle \propto e^.$

The partition function is the volume of configurations, each configuration weighted by its Boltzmann weight. Since each configuration is described by the sign-changes, the partition function factorizes:

$Z = \sum_ e^ = \prod_k (1 + p ) = (1 + p)^L.$

The logarithm divided by ''L'' is the free energy density:

$\beta f = \log(1 + p) = \log\left(1 + \frac\right),$

which is analytic away from β = ∞. A sign of a phase transition is a non-analytic free energy, so the one-dimensional model does not have a phase transition.

One-dimensional solution with transverse field

To express the Ising Hamiltonian using a quantum mechanical description of spins, we replace the spin variables with their respective Pauli matrices. However, depending on the direction of the magnetic field, we can create a transverse-field or longitudinal-field Hamiltonian. The transverse-field Hamiltonian is given by

$H(\sigma) = -J \sum_ \sigma_i^z \sigma_^z - h \sum_i \sigma_i^x.$

The transverse-field model experiences a phase transition between an ordered and disordered regime at ''J'' ~ ''h''. This can be shown by a mapping of Pauli matrices

$\sigma_n^z = \prod_^n T_i^x,$

$\sigma_n^x = T_n^z T_^z.$

Upon rewriting the Hamiltonian in terms of this change-of-basis matrices, we obtain

$H(\sigma) = -h \sum_ T_i^z T_^z - J \sum_i T_i^x.$

Since the roles of ''h'' and ''J'' are switched, the Hamiltonian undergoes a transition at ''J'' = ''h''.

Renormalization

When there is no external field, we can derive a functional equation that $f(\beta, 0) = f(\beta)$ satisfies using renormalization. Specifically, let $Z_N(\beta, J)$ be the partition function with $N$ sites. Now we have:$Z_N(\beta, J) = \sum_ e^e^\cdots$where $K := \beta J$. We sum over each of $\sigma_2, \sigma_4, \cdots$, to obtain$Z_N(\beta, J) = \sum_ (2\cosh(K(\sigma_1 + \sigma_3))) \cdot (2\cosh(K(\sigma_3 + \sigma_5))) \cdots$Now, since the cosh function is even, we can solve $Ae^ = 2\cosh(K(\sigma_1+\sigma_3))$ as $A = 2\sqrt, K' = \frac 12 \ln\cosh(2K)$. Now we have a self-similarity relation:$\frac 1N \ln Z_N(K) = \frac 12 \ln\left(2\sqrt\right) + \frac 12 \frac \ln Z_(K')$Taking the limit, we obtain$f(\beta) = \frac 12 \ln\left(2\sqrt\right) + \frac 12 f(\beta')$where $\beta' J = \frac 12 \ln\cosh(2\beta J)$.

When $\beta$ is small, we have $f(\beta)\approx \ln 2$, so we can numerically evaluate $f(\beta)$ by iterating the functional equation until $K$ is small.

Two dimensions

In the ferromagnetic case there is a phase transition. At low temperature, the Peierls argument proves positive magnetization for the nearest neighbor case and then, by the Griffiths inequality, also when longer range interactions are added. Meanwhile, at high temperature, the cluster expansion gives analyticity of the thermodynamic functions. In the nearest-neighbor case, the free energy was exactly computed by Onsager. The spin-spin correlation functions were computed by McCoy and Wu.

Onsager's exact solution

obtained the following analytical expression for the free energy of the Ising model on the anisotropic square lattice when the magnetic field $h=0$ in the thermodynamic limit as a function of temperature and the horizontal and vertical interaction energies $J_1$ and $J_2$, respectively

-\beta f = \ln 2 + \frac\int_0^d\theta_1\int_0^d\theta_2 \ln cosh(2\beta J_1)\cosh(2\beta J_2) -\sinh(2\beta J_1)\cos(\theta_1)-\sinh(2\beta J_2)\cos(\theta_2)

From this expression for the free energy, all thermodynamic functions of the model can be calculated by using an appropriate derivative. The 2D Ising model was the first model to exhibit a continuous phase transition at a positive temperature. It occurs at the temperature $T_c$ which solves the equation

$\sinh\left(\frac\right)\sinh\left(\frac\right) = 1.$

In the isotropic case when the horizontal and vertical interaction energies are equal $J_1=J_2=J$, the critical temperature $T_c$ occurs at the following point

$T_c = \frac = (2.269185\cdots)\frac$

When the interaction energies $J_1$, $J_2$ are both negative, the Ising model becomes an antiferromagnet. Since the square lattice is bi-partite, it is invariant under this change when the magnetic field $h=0$, so the free energy and critical temperature are the same for the antiferromagnetic case. For the triangular lattice, which is not bi-partite, the ferromagnetic and antiferromagnetic Ising model behave notably differently. Specifically, around a triangle, it is impossible to make all 3 spin-pairs antiparallel, so the antiferromagnetic Ising model cannot reach the minimal energy state. This is an example of geometric frustration.

= Onsager's formula for spontaneous magnetization

=

Onsager famously announced the following expression for the spontaneous magnetization ''M'' of a two-dimensional Ising ferromagnet on the square lattice at two different conferences in 1948, though without proof

M = \left(1 - \left sinh 2\beta J_1 \sinh 2\beta J_2\right\right)^

where $J_1$ and $J_2$ are horizontal and vertical interaction energies.

A complete derivation was only given in 1951 by using a limiting process of transfer matrix eigenvalues. The proof was subsequently greatly simplified in 1963 by Montroll, Potts, and Ward using Szegő's limit formula for Toeplitz determinants by treating the magnetization as the limit of correlation functions.

Minimal model

At the critical point, the two-dimensional Ising model is a two-dimensional conformal field theory. The spin and energy correlation functions are described by a minimal model, which has been exactly solved.

Three dimensions

In three as in two dimensions, the most studied case of the Ising model is the translation-invariant model on a cubic lattice with nearest-neighbor coupling in the zero magnetic field. Many theoreticians searched for an analytical three-dimensional solution for many decades, which would be analogous to Onsager's solution in the two-dimensional case. Such a solution has not been found until now, although there is no proof that it may not exist. In three dimensions, the Ising model was shown to have a representation in terms of non-interacting fermionic strings by Alexander Polyakov and Vladimir Dotsenko. This construction has been carried on the lattice, and the continuum limit, conjecturally describing the critical point, is unknown.

In three as in two dimensions, Peierls' argument shows that there is a phase transition. This phase transition is rigorously known to be continuous (in the sense that correlation length diverges and the magnetization goes to zero), and is called the critical point. It is believed that the critical point can be described by a renormalization group fixed point of the Wilson-Kadanoff renormalization group transformation. It is also believed that the phase transition can be described by a three-dimensional unitary conformal field theory, as evidenced by Monte Carlo simulations, exact diagonalization results in quantum models, and quantum field theoretical arguments. Although it is an open problem to establish rigorously the renormalization group picture or the conformal field theory picture, theoretical physicists have used these two methods to compute the critical exponents of the phase transition, which agree with the experiments and with the Monte Carlo simulations. This conformal field theory describing the three-dimensional Ising critical point is under active investigation using the method of the conformal bootstrap. This method currently yields the most precise information about the structure of the critical theory (see Ising critical exponents).

In 2000, Sorin Istrail of Sandia National Laboratories proved that the spin glass Ising model on a nonplanar lattice is NP-complete. That is, assuming P ≠ NP, the general spin glass Ising model is exactly solvable only in planar cases, so solutions for dimensions higher than two are also intractable. Istrail's result only concerns the spin glass model with spatially varying couplings, and tells nothing about Ising's original ferromagnetic model with equal couplings.

Four dimensions and above

In any dimension, the Ising model can be productively described by a locally varying mean field. The field is defined as the average spin value over a large region, but not so large so as to include the entire system. The field still has slow variations from point to point, as the averaging volume moves. These fluctuations in the field are described by a continuum field theory in the infinite system limit. The accuracy of this approximation improves as the dimension becomes larger. A deeper understanding of how the Ising model behaves, going beyond mean-field approximations, can be achieved using renormalization group methods.

See also

* ANNNI model
* Binder parameter
* Boltzmann machine
* Construction of an irreducible Markov chain in the Ising model
* Geometrical frustration
* Classical Heisenberg model
* Quantum Heisenberg model
* Kuramoto model
* Maximal evenness
* Order operator
* Spin model
* t-J model
* Classical XY model
* ZN model

Footnotes

References

*
*
*
*
*
*
*
*
*
*
*
* Ross Kindermann and J. Laurie Snell (1980),
Markov Random Fields and Their Applications
'. American Mathematical Society. .
* Kleinert, H (1989), ''Gauge Fields in Condensed Matter'', Vol. I, "Superflow and Vortex Lines", pp. 1–742, Vol. II, "Stresses and Defects", pp. 743–1456,
World Scientific (Singapore)
Paperback '' (also available online

an

''
* Kleinert, H and Schulte-Frohlinde, V (2001), ''Critical Properties of φ⁴-Theories''
World Scientific (Singapore)
Paperback '' (also availabl
online
''
*
* Barry M. McCoy and Tai Tsun Wu (1973), ''The Two-Dimensional Ising Model''. Harvard University Press, Cambridge Massachusetts,
*
*
*
* John Palmer (2007), ''Planar Ising Correlations''. Birkhäuser, Boston, .
*
*
*
*
*
*
*

External links

* Barry Arthur Cipra, "The Ising model is NP-complete", SIAM News, Vol. 33, No. 6
online edition (.pdf)





A dynamical 2D Ising java applet




“I sing well-tempered” The Ising Model: A simple model for critical behavior in a system of spins
by Dirk Brockman, is an interactive simulation that allows users to export the working code to a presentation slide

Ising Model simulation
by Enrique Zeleny, the Wolfram Demonstrations Project

Phase transitions on lattices


* ttp://isingspinwebgl.com Interactive Monte Carlo simulation of the Ising, XY and Heisenberg models with 3D graphics (requires WebGL compatible browser)
Ising Model code image denoising example with Ising Model

David Tong's Lecture Notes
provide a good introduction

The Cartoon Picture of Magnets That Has Transformed Science
- Quanta Magazine article about Ising model
*Simulation of the 2-dimensional Ising model in Julia: https://github.com/cossio/SquareIsingModel.jl

{{DEFAULTSORT:Ising Model
Spin models
Exactly solvable models
Statistical mechanics
Lattice models
NP-complete problems