|
Detailed Balance
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes (collisions, or steps, or elementary reactions). It states that at equilibrium, each elementary process is in equilibrium with its reverse process. History The principle of detailed balance was explicitly introduced for collisions by Ludwig Boltzmann. In 1872, he proved his H-theorem using this principle.Boltzmann, L. (1964), Lectures on gas theory, Berkeley, CA, USA: U. of California Press. The arguments in favor of this property are founded upon microscopic reversibility. Tolman, R. C. (1938). ''The Principles of Statistical Mechanics''. Oxford University Press, London, UK. Five years before Boltzmann, James Clerk Maxwell used the principle of detailed balance for gas kinetics with the reference to the principle of sufficient reason. He compared the idea of detailed balance with other types of balancing (like cyclic balance) and found that "Now it is impossible to as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetics (physics)
In physics and engineering, kinetics is the branch of classical mechanics that is concerned with the relationship between the motion and its causes, specifically, forces and torques. Since the mid-20th century, the term " dynamics" (or "analytical dynamics") has largely superseded "kinetics" in physics textbooks, though the term is still used in engineering. In plasma physics, kinetics refers to the study of continua in velocity space. This is usually in the context of non-thermal ( non-Maxwellian) velocity distributions, or processes that perturb thermal distributions. These " kinetic plasmas" cannot be adequately described with fluid equations. The term ''kinetics'' is also used to refer to chemical kinetics, particularly in chemical physics and physical chemistry Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Nikolaevich Gorban
Alexander Nikolaevich Gorban (russian: Александр Николаевич Горба́нь) is a scientist of Russian origin, working in the United Kingdom. He is a professor at the University of Leicester, and director of its Mathematical Modeling Centre. Gorban has contributed to many areas of fundamental and applied science, including statistical physics, non-equilibrium thermodynamics, machine learning and mathematical biology. Gorban is the author of about 20 books and 300 scientific publications. He has founded several scientific schools in the areas of physical and chemical kinetics, dynamical systems theory and artificial neural networks, and is ranked as one of the 1000 most cited researchers of Russian origin.According to http://www.scientific.ru/ , 2012 Gorban has supervised 6 habilitations and more than 30 PhD theses. Biography Alexander N. Gorban was born in Omsk on 19 April 1952. His father Nikolai Vasilievich Gorban was a historian and writer exiled to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American people, American mathematician, electrical engineering, electrical engineer, and cryptography, cryptographer known as a "father of information theory". As a 21-year-old master's degree student at the Massachusetts Institute of Technology (MIT), he wrote A Symbolic Analysis of Relay and Switching Circuits, his thesis demonstrating that electrical applications of Boolean algebra could construct any logical numerical relationship. Shannon contributed to the field of cryptanalysis for national defense of the United States during World War II, including his fundamental work on codebreaking and secure telecommunications. Biography Childhood The Shannon family lived in Gaylord, Michigan, and Claude was born in a hospital in nearby Petoskey, Michigan, Petoskey. His father, Claude Sr. (1862–1934), was a businessman and for a while, a judge of probate in Gaylord. His mother, Mabel Wolf Shannon (1890–1945), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hendrik Lorentz
Hendrik Antoon Lorentz (; 18 July 1853 – 4 February 1928) was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect. He also derived the Lorentz transformation underpinning Albert Einstein's special theory of relativity, as well as the Lorentz force, which describes the combined electric and magnetic forces acting on a charged particle in an electromagnetic field. Lorentz was also responsible for the Lorentz oscillator model, a classical model used to describe the anomalous dispersion observed in dielectric materials when the driving frequency of the electric field was near the resonant frequency, resulting in abnormal refractive indices. According to the biography published by the Nobel Foundation, "It may well be said that Lorentz was regarded by all theoretical physicists as the world's leading spirit, who completed what was left unfinished by his predecessors and prepared t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
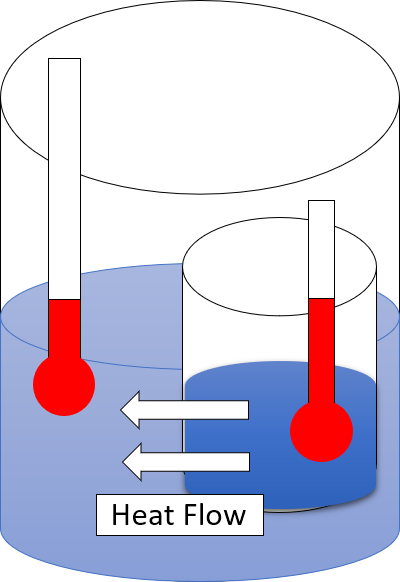
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and Energy transformation, energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unless energy in some form is supplied to reverse the direction of heat flow. Another definition is: "Not all heat energy can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics in other versions establishes the concept of entropy as a physical property of a thermodynamic system. It can be used to predict whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. The second law may be formulated by the observation that the entropy of isolated systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aizik Isaakovich Vol'pert
Aizik Isaakovich Vol'pert (russian: Айзик Исаакович Вольперт) (5 June 1923 – January 2006) (the family name is also transliterated as Volpert or WolpertSee .) was a Soviet and Israeli mathematician and chemical engineer working in partial differential equations, functions of bounded variation and chemical kinetics. Life and academic career Vol'pert graduated from Lviv University in 1951, earning the candidate of science degree and the docent title respectively in 1954 and 1956 from the same university: from 1951 on he worked at the Lviv Industrial Forestry Institute. In 1961 he became senior research fellow while 1962 he earned the "doktor nauk" degree from Moscow State University. In the 1970s–1980s A. I. Volpert became one of the leaders of the Russian Mathematical Chemistry scientific community. He finally joined Technion’s Faculty of Mathematics in 1993, doing his Aliyah in 1994. Work Index theory and elliptic boundary problems Vol'pert de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete-time Markov Chain
In probability, a discrete-time Markov chain (DTMC) is a sequence of random variables, known as a stochastic process, in which the value of the next variable depends only on the value of the current variable, and not any variables in the past. For instance, a machine may have two states, ''A'' and ''E''. When it is in state ''A'', there is a 40% chance of it moving to state ''E'' and a 60% chance of it remaining in state ''A''. When it is in state ''E'', there is a 70% chance of it moving to ''A'' and a 30% chance of it staying in ''E''. The sequence of states of the machine is a Markov chain. If we denote the chain by X_0, X_1, X_2, ... then X_0 is the state which the machine starts in and X_ is the random variable describing its state after 10 transitions. The process continues forever, indexed by the natural numbers. An example of a stochastic process which is not a Markov chain is the model of a machine which has states ''A'' and ''E'' and moves to ''A'' from either state w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov's Criterion
In probability theory, Kolmogorov's criterion, named after Andrey Kolmogorov, is a theorem giving a necessary and sufficient condition for a Markov chain or continuous-time Markov chain to be stochastically identical to its time-reversed version. Discrete-time Markov chains The theorem states that an irreducible, positive recurrent, aperiodic Markov chain with transition matrix ''P'' is reversible if and only if its stationary Markov chain satisfies : p_ p_ \cdots p_ p_ = p_ p_ \cdots p_ p_ for all finite sequences of states : j_1, j_2, \ldots, j_n \in S . Here ''pij'' are components of the transition matrix ''P'', and ''S'' is the state space of the chain. Example Consider this figure depicting a section of a Markov chain with states ''i'', ''j'', ''k'' and ''l'' and the corresponding transition probabilities. Here Kolmogorov's criterion implies that the product of probabilities when traversing through any closed loop must be equal, so the product around the loop ''i'' t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Distribution
Stationary distribution may refer to: * A special distribution for a Markov chain such that if the chain starts with its stationary distribution, the marginal distribution of all states at any time will always be the stationary distribution. Assuming irreducibility, the stationary distribution is always unique if it exists, and its existence can be implied by positive recurrence of all states. The stationary distribution has the interpretation of the limiting distribution when the chain is irreducible and aperiodic. * The marginal distribution of a stationary process or stationary time series * The set of joint probability distributions of a stationary process or stationary time series In some fields of application, the term stable distribution is used for the equivalent of a stationary (marginal) distribution, although in probability and statistics the term has a rather different meaning: see stable distribution. Crudely stated, all of the above are specific cases of a common ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Probability
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Process
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
