|
Quasiprojective Variety
In mathematics, a quasi-projective variety in algebraic geometry is a locally closed subset of a projective variety, i.e., the intersection inside some projective space of a Zariski-open and a Zariski-closed subset. A similar definition is used in scheme theory, where a ''quasi-projective scheme'' is a locally closed subscheme of some projective space. Relationship to affine varieties An affine space is a Zariski-open subset of a projective space, and since any closed affine subset U can be expressed as an intersection of the projective completion \bar and the affine space embedded in the projective space, this implies that any affine variety is quasiprojective. There are locally closed subsets of projective space that are not affine, so that quasi-projective is more general than affine. Taking the complement of a single point in projective space of dimension at least 2 gives a non-affine quasi-projective variety. This is also an example of a quasi-projective variety that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Polynomial
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial x^3 + 3 x^2 y + z^7 is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function. An algebraic form, or simply form, is a function defined by a homogeneous polynomial. A binary form is a form in two variables. A ''form'' is also a function defined on a vector space, which may be expressed as a homogeneous function of the coordinates over any basis. A polynomial of degree 0 is always homogeneous; it is simply an element of the field or ring of the coefficients, usually called a constant or a scalar. A form of degree 1 is a linear form. A form of degree 2 is a quad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisorial Scheme
In algebraic geometry, a divisorial scheme is a scheme admitting an ample family of line bundles, as opposed to an ample line bundle. In particular, a quasi-projective variety is a divisorial scheme and the notion is a generalization of "quasi-projective". It was introduced in (in the case of a variety) as well as in (in the case of a scheme). The term "divisorial" refers to the fact that "the topology of these varieties is determined by their positive divisors." The class of divisorial schemes is quite large: it includes affine schemes, separated regular (noetherian) schemes and subschemes of a divisorial scheme (such as projective varieties). Definition Here is the definition in SGA 6, which is a more general version of the definition of Borelli. Given a quasi-compact quasi-separated scheme ''X'', a family of invertible sheaves L_i, i \in I on it is said to be an ample family if the open subsets U_f = \, f \in \Gamma(X, L_i^), i \in I, n \ge 1 form a base of the (Zariski) top ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Algebraic Variety
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition. Conventions regarding the definition of an algebraic variety differ slightly. For example, some definitions require an algebraic variety to be irreducible, which means that it is not the union of two smaller sets that are closed in the Zariski topology. Under this definition, non-irreducible algebraic varieties are called algebraic sets. Other conventions do not require irreducibility. The fundamental theorem of algebra establishes a link between algebra and geometry by showing that a monic polynomial (an algebraic object) in one variable with complex number coefficients is determin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (paral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
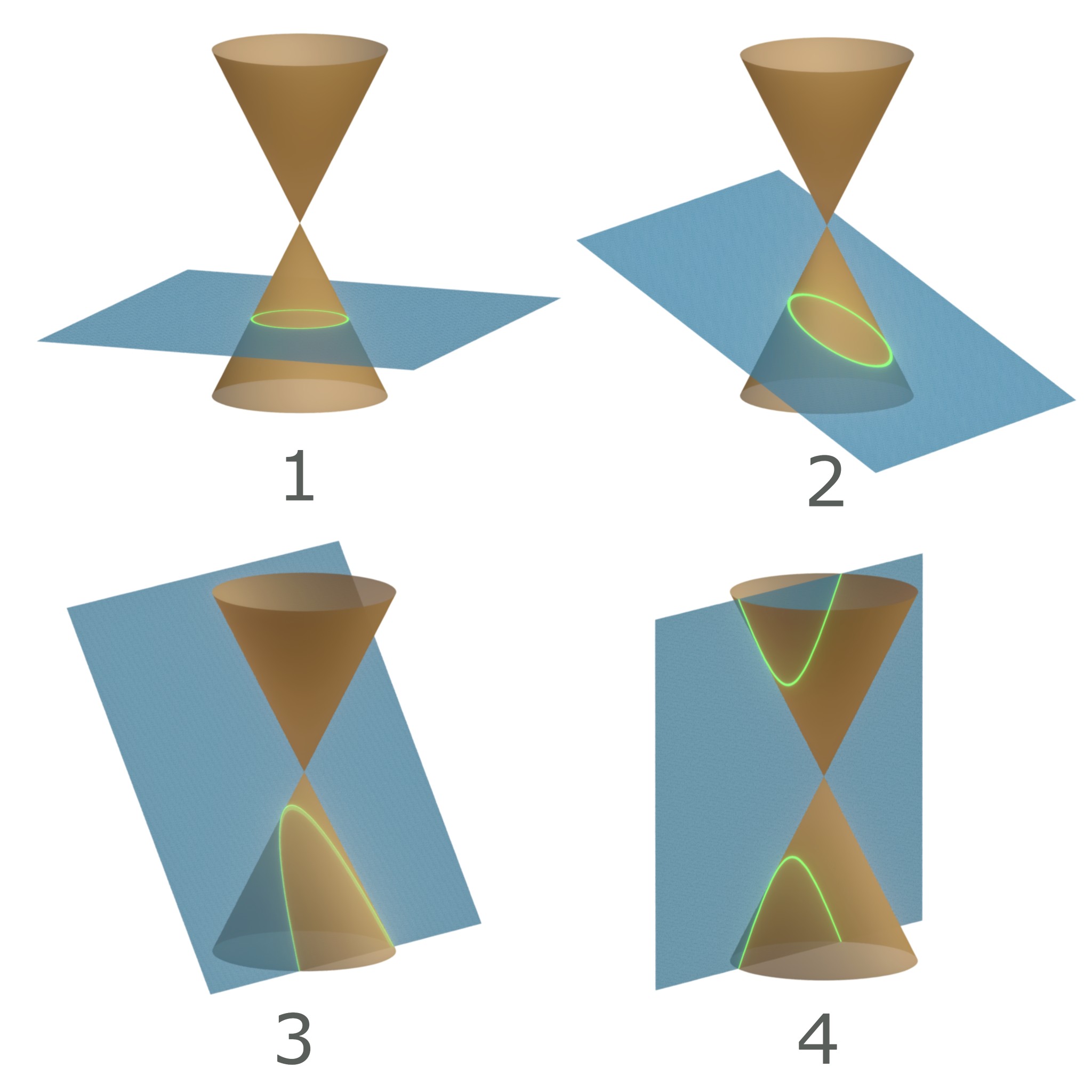
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Closed
In topology, a branch of mathematics, a subset E of a topological space X is said to be locally closed if any of the following equivalent conditions are satisfied: * E is the intersection of an open set and a closed set in X. * For each point x\in E, there is a neighborhood U of x such that E \cap U is closed in U. * E is an open subset of its closure \overline. * The set \overline\setminus E is closed in X. * E is the difference of two closed sets in X. * E is the difference of two open sets in X. The second condition justifies the terminology ''locally closed'' and is Bourbaki's definition of locally closed. To see the second condition implies the third, use the facts that for subsets A \subseteq B, A is closed in B if and only if A = \overline \cap B and that for a subset E and an open subset U, \overline \cap U = \overline \cap U. Examples The interval (0, 1] = (0, 2) \cap , 1 The comma is a punctuation mark that appears in several variants in different languages. It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Variety
In algebraic geometry, an affine variety, or affine algebraic variety, over an algebraically closed field is the zero-locus in the affine space of some finite family of polynomials of variables with coefficients in that generate a prime ideal. If the condition of generating a prime ideal is removed, such a set is called an (affine) algebraic set. A Zariski open subvariety of an affine variety is called a quasi-affine variety. Some texts do not require a prime ideal, and call ''irreducible'' an algebraic variety defined by a prime ideal. This article refers to zero-loci of not necessarily prime ideals as affine algebraic sets. In some contexts, it is useful to distinguish the field in which the coefficients are considered, from the algebraically closed field (containing ) over which the zero-locus is considered (that is, the points of the affine variety are in ). In this case, the variety is said ''defined over'' , and the points of the variety that belong to are said ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Space
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. In an affine space, there are instead '' displacement vectors'', also called ''translation'' vectors or simply ''translations'', between two points of the space. Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. Any vector space may be viewed as an affine s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros. The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscates and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry Of Projective Spaces
Projective space plays a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of projective space. Homogeneous polynomial ideals Let k be an algebraically closed field, and ''V'' be a finite-dimensional vector space over k. The symmetric algebra of the dual vector space ''V*'' is called the polynomial ring on ''V'' and denoted by k 'V'' It is a naturally graded algebra by the degree of polynomials. The projective Nullstellensatz states that, for any homogeneous ideal ''I'' that does not contain all polynomials of a certain degree (referred to as an irrelevant ideal), the common zero locus of all polynomials in ''I'' (or ''Nullstelle'') is non-trivial (i.e. the common zero locus contains more than the single element ), and, more precisely, the ideal of polynomials that vanish on that locus coincides with the radical of the ideal ''I''. This last assertion is best summarized by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |