|
Power-law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four. Empirical examples The distributions of a wide variety of physical, biological, and man-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the species richness in clades of organisms, the sizes of power outages, volcanic eruptions, human judgments of stimulus intensity and many other qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustic Attenuation
Acoustic attenuation is a measure of the energy loss of sound propagation in media. Most media have viscosity and are therefore not ideal media. When sound propagates in such media, there is always thermal consumption of energy caused by viscosity. This effect can be quantified through the Stokes's law of sound attenuation. Sound attenuation may also be a result of heat conductivity in the media as has been shown by G. Kirchhoff in 1868. The Stokes-Kirchhoff attenuation formula takes into account both viscosity and thermal conductivity effects. For heterogeneous media, besides media viscosity, acoustic scattering is another main reason for removal of acoustic energy. Acoustic attenuation in a lossy medium plays an important role in many scientific researches and engineering fields, such as medical ultrasonography, vibration and noise reduction. Power-law frequency-dependent acoustic attenuation Many experimental and field measurements show that the acoustic attenuation coeffici ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Invariance
In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality. The technical term for this transformation is a dilatation (also known as dilation), and the dilatations can also form part of a larger conformal symmetry. *In mathematics, scale invariance usually refers to an invariance of individual functions or curves. A closely related concept is self-similarity, where a function or curve is invariant under a discrete subset of the dilations. It is also possible for the probability distributions of random processes to display this kind of scale invariance or self-similarity. *In classical field theory, scale invariance most commonly applies to the invariance of a whole theory under dilatations. Such theories typically describe classical physical processes with no characteristic length scale. *In quantum field the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Outage
A power outage (also called a powercut, a power out, a power failure, a power blackout, a power loss, or a blackout) is the loss of the electrical power network supply to an end user. There are many causes of power failures in an electricity network. Examples of these causes include faults at power stations, damage to electric transmission lines, substations or other parts of the distribution system, a short circuit, cascading failure, fuse or circuit breaker operation. Power failures are particularly critical at sites where the environment and public safety are at risk. Institutions such as hospitals, sewage treatment plants, and mines will usually have backup power sources such as standby generators, which will automatically start up when electrical power is lost. Other critical systems, such as telecommunication, are also required to have emergency power. The battery room of a telephone exchange usually has arrays of lead–acid batteries for backup and also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-normal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as McAlister, Gibrat and Cobb–Douglas. A log-normal process is the statistical realization of the multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
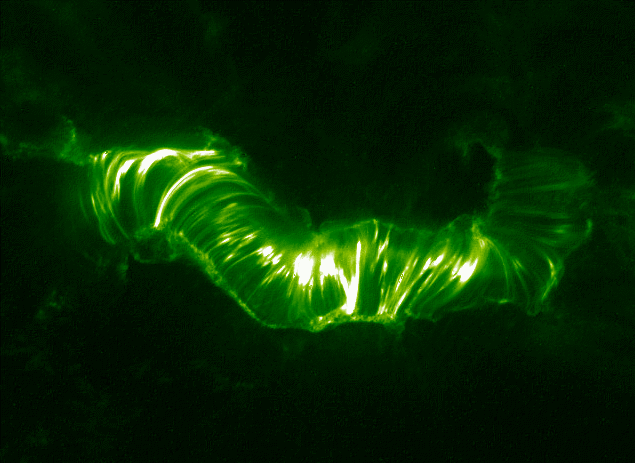
Solar Flare
A solar flare is an intense localized eruption of electromagnetic radiation in the Sun's atmosphere. Flares occur in active regions and are often, but not always, accompanied by coronal mass ejections, solar particle events, and other solar phenomena. The occurrence of solar flares varies with the 11-year solar cycle. Solar flares are thought to occur when stored magnetic energy in the Sun's atmosphere accelerates charged particles in the surrounding plasma. This results in the emission of electromagnetic radiation across the electromagnetic spectrum. High-energy electromagnetic radiation from solar flares is absorbed by the daylight side of Earth's upper atmosphere, in particular the ionosphere, and does not reach the surface. This absorption can temporarily increase the ionization of the ionosphere which may interfere with short-wave radio communication. The prediction of solar flares is an active area of research. Flares also occur on other stars, where the term ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allometric Scaling
Allometry is the study of the relationship of body size to shape, anatomy, physiology and finally behaviour, first outlined by Otto Snell in 1892, by D'Arcy Thompson in 1917 in '' On Growth and Form'' and by Julian Huxley in 1932. Overview Allometry is a well-known study, particularly in statistical shape analysis for its theoretical developments, as well as in biology for practical applications to the differential growth rates of the parts of a living organism's body. One application is in the study of various insect species (e.g., Hercules beetles), where a small change in overall body size can lead to an enormous and disproportionate increase in the dimensions of appendages such as legs, antennae, or horns The relationship between the two measured quantities is often expressed as a power law equation (Allometric equation) which expresses a remarkable scale symmetry: : y = kx^a \,\! or in a logarithmic form: : \log y = a \log x + \log k\,\! or similarly \ln y = a \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto ( ), is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value () of log45 ≈ 1.16 precisely reflect it. Empirical observation has shown that this 80-20 distribution fits a wide range of cases, including natural phenomena and human activities. Definitions If ''X'' is a random variable with a Pareto (Type I) distribution, then the probability that ''X'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Swan Theory
The black swan theory or theory of black swan events is a metaphor that describes an event that comes as a surprise, has a major effect, and is often inappropriately rationalized after the fact with the benefit of hindsight. The term is based on an ancient saying that presumed black swans did not exist a saying that became reinterpreted to teach a different lesson after they were discovered in Australia. The theory was developed by Nassim Nicholas Taleb, starting in 2001, to explain: # The disproportionate role of high-profile, hard-to-predict, and rare events that are beyond the realm of normal expectations in history, science, finance, and technology. # The non-computability of the probability of consequential rare events using scientific methods (owing to the very nature of small probabilities). # The psychological biases that blind people, both individually and collectively, to uncertainty and a rare event's massive role in historical affairs. Taleb's "black swan theory" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
YouTube
YouTube is a global online video sharing and social media platform headquartered in San Bruno, California. It was launched on February 14, 2005, by Steve Chen, Chad Hurley, and Jawed Karim. It is owned by Google, and is the second most visited website, after Google Search. YouTube has more than 2.5 billion monthly users who collectively watch more than one billion hours of videos each day. , videos were being uploaded at a rate of more than 500 hours of content per minute. In October 2006, YouTube was bought by Google for $1.65 billion. Google's ownership of YouTube expanded the site's business model, expanding from generating revenue from advertisements alone, to offering paid content such as movies and exclusive content produced by YouTube. It also offers YouTube Premium, a paid subscription option for watching content without ads. YouTube also approved creators to participate in Google's AdSense program, which seeks to generate more revenue for both parties. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Tail
In statistics and business, a long tail of some distributions of numbers is the portion of the distribution having many occurrences far from the "head" or central part of the distribution. The distribution could involve popularities, random numbers of occurrences of events with various probabilities, etc. The term is often used loosely, with no definition or an arbitrary definition, but precise definitions are possible. In statistics, the term ''long-tailed distribution'' has a narrow technical meaning, and is a subtype of heavy-tailed distribution. Intuitively, a distribution is (right) long-tailed if, for any fixed amount, when a quantity exceeds a high level, it almost certainly exceeds it by at least that amount: large quantities are probably even larger. Note that there is no sense of ''the'' "long tail" of a distribution, but only the ''property'' of a distribution being long-tailed. In business, the term ''long tail'' is applied to rank-size distributions or rank-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
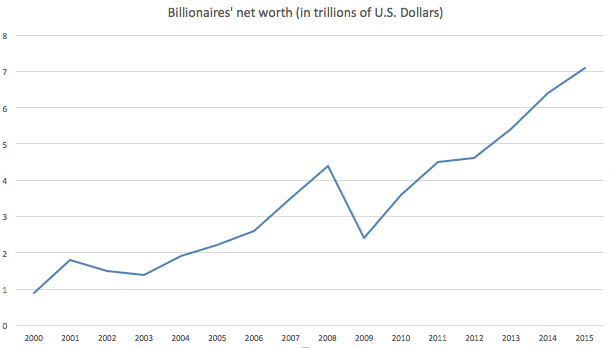
World's Richest Person
''The World's Billionaires'' is an annual ranking by documented net worth of the wealthiest billionaires in the world, compiled and published in March annually by the American business magazine '' Forbes''. The list was first published in March 1987. The total net worth of each individual on the list is estimated and is cited in United States dollars, based on their documented assets and accounting for debt and other factors. Royalty and dictators whose wealth comes from their positions are excluded from these lists. This ranking is an index of the wealthiest documented individuals, excluding any ranking of those with wealth that is not able to be completely ascertained. In 2018, Amazon founder Jeff Bezos was ranked at the top for the first time and became the first centibillionaire included in the ranking, surpassing Microsoft founder Bill Gates, who had topped the list 18 of the previous 24 years. In 2022, after topping the list for four years, Bezos was surpassed by El ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |