|
Polarization Identities
In linear algebra, a branch of mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. If a norm arises from an inner product then the polarization identity can be used to express this inner product entirely in terms of the norm. The polarization identity shows that a norm can arise from at most one inner product; however, there exist norms that do not arise from any inner product. The norm associated with any inner product space satisfies the parallelogram law: \, x+y\, ^2 + \, x-y\, ^2 = 2\, x\, ^2 + 2\, y\, ^2. In fact, as observed by John von Neumann, the parallelogram law characterizes those norms that arise from inner products. Given a normed space (H, \, \cdot\, ), the parallelogram law holds for \, \cdot\, if and only if there exists an inner product \langle \cdot, \cdot \rangle on H such that \, x\, ^2 = \langle x,\ x\rangle for all x \in H, in which case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram Law
In mathematics, the simplest form of the parallelogram law (also called the parallelogram identity) belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals. We use these notations for the sides: ''AB'', ''BC'', ''CD'', ''DA''. But since in Euclidean geometry a parallelogram necessarily has opposite sides equal, that is, ''AB'' = ''CD'' and ''BC'' = ''DA'', the law can be stated as 2AB^2 + 2BC^2 = AC^2 + BD^2\, If the parallelogram is a rectangle, the two diagonals are of equal lengths ''AC'' = ''BD'', so 2AB^2 + 2BC^2 = 2AC^2 and the statement reduces to the Pythagorean theorem. For the general quadrilateral with four sides not necessarily equal, AB^2 + BC^2 + CD^2+DA^2 = AC^2+BD^2 + 4x^2, where x is the length of the line segment joining the midpoints of the diagonals. It can be seen from the diagram that x = 0 for a parallelogram, and so the ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Bilinear Form
In mathematics, a symmetric bilinear form on a vector space is a bilinear map from two copies of the vector space to the field of scalars such that the order of the two vectors does not affect the value of the map. In other words, it is a bilinear function B that maps every pair (u,v) of elements of the vector space V to the underlying field such that B(u,v)=B(v,u) for every u and v in V. They are also referred to more briefly as just symmetric forms when "bilinear" is understood. Symmetric bilinear forms on finite-dimensional vector spaces precisely correspond to symmetric matrices given a basis for ''V''. Among bilinear forms, the symmetric ones are important because they are the ones for which the vector space admits a particularly simple kind of basis known as an orthogonal basis (at least when the characteristic of the field is not 2). Given a symmetric bilinear form ''B'', the function is the associated quadratic form on the vector space. Moreover, if the characteristic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non- collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
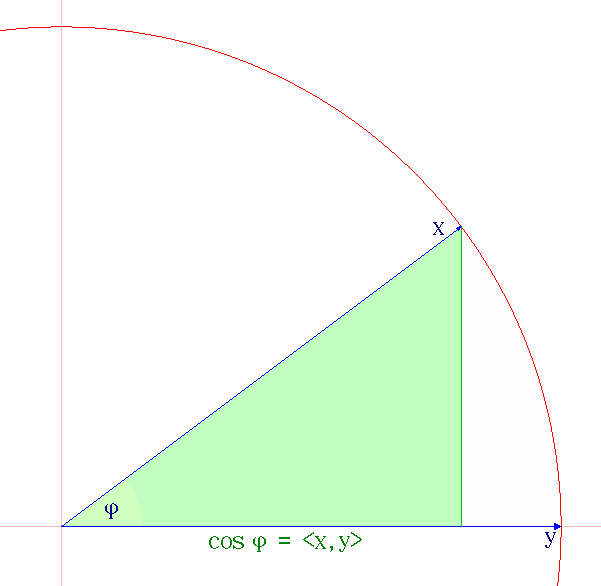
Law Of Cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states :c^2 = a^2 + b^2 - 2ab\cos\gamma, where denotes the angle contained between sides of lengths and and opposite the side of length . For the same figure, the other two relations are analogous: :a^2=b^2+c^2-2bc\cos\alpha, :b^2=a^2+c^2-2ac\cos\beta. The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle is a right angle (of measure 90 degrees, or radians), then , and thus the law of cosines reduces to the Pythagorean theorem: :c^2 = a^2 + b^2. The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known. History Though the notion of the cosine was not yet developed in his time, Euclid's ''Elements'', dating back to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotation), or a composition of a rigid motion and a reflection. Isometries are often used in constructions where one spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) '' endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy's Inequality
In Euclidean geometry, Ptolemy's inequality relates the six distances determined by four points in the plane or in a higher-dimensional space. It states that, for any four points , , , and , the following inequality holds: :\overline\cdot \overline+\overline\cdot \overline \ge \overline\cdot \overline. It is named after the Greek astronomer and mathematician Ptolemy. The four points can be ordered in any of three distinct ways (counting reversals as not distinct) to form three different quadrilaterals, for each of which the sum of the products of opposite sides is at least as large as the product of the diagonals. Thus the three product terms in the inequality can be additively permuted to put any one of them on the right side of the inequality, so the three products of opposite sides or of diagonals of any one of the quadrilaterals must obey the triangle inequality.. As a special case, Ptolemy's theorem states that the inequality becomes an equality when the four points lie in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Zero
In mathematics, the characteristic of a ring , often denoted , is defined to be the smallest number of times one must use the ring's multiplicative identity (1) in a sum to get the additive identity (0). If this sum never reaches the additive identity the ring is said to have characteristic zero. That is, is the smallest positive number such that: :\underbrace_ = 0 if such a number exists, and otherwise. Motivation The special definition of the characteristic zero is motivated by the equivalent definitions characterized in the next section, where the characteristic zero is not required to be considered separately. The characteristic may also be taken to be the exponent of the ring's additive group, that is, the smallest positive integer such that: :\underbrace_ = 0 for every element of the ring (again, if exists; otherwise zero). Some authors do not include the multiplicative identity element in their requirements for a ring (see Multiplicative identity and the t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Bilinear Form
In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix * Positive-definite quadratic form In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite ... References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real And Imaginary Parts Of A Linear Functional
In mathematics, a linear form (also known as a linear functional, a one-form, or a covector) is a linear map from a vector space to its field of scalars (often, the real numbers or the complex numbers). If is a vector space over a field , the set of all linear functionals from to is itself a vector space over with addition and scalar multiplication defined pointwise. This space is called the dual space of , or sometimes the algebraic dual space, when a topological dual space is also considered. It is often denoted , p. 19, §3.1 or, when the field is understood, V^*; other notations are also used, such as V', V^ or V^. When vectors are represented by column vectors (as is common when a basis is fixed), then linear functionals are represented as row vectors, and their values on specific vectors are given by matrix products (with the row vector on the left). Examples * The constant zero function, mapping every vector to zero, is trivially a linear functional. * Indexing in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |