|
Phase Transfer Function
The optical transfer function (OTF) of an optical system such as a camera, microscope, human eye, or projector specifies how different spatial frequencies are captured or transmitted. It is used by optical engineers to describe how the optics project light from the object or scene onto a photographic film, detector array, retina, screen, or simply the next item in the optical transmission chain. A variant, the modulation transfer function (MTF), neglects phase effects, but is equivalent to the OTF in many situations. Either transfer function specifies the response to a periodic sine-wave pattern passing through the lens system, as a function of its spatial frequency or period, and its orientation. Formally, the OTF is defined as the Fourier transform of the point spread function (PSF, that is, the impulse response of the optics, the image of a point source). As a Fourier transform, the OTF is complex-valued; but it will be real-valued in the common case of a PSF that is symmetr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
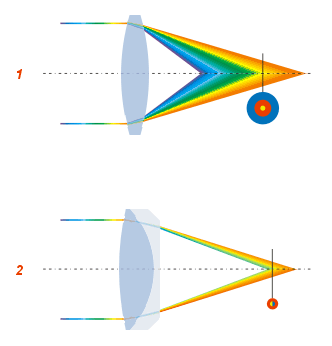
Illustration Of The Optical Transfer Function And Its Relation To Image Quality
An illustration is a decoration, interpretation or visual explanation of a text, concept or process, designed for integration in print and digital published media, such as posters, Flyer (pamphlet), flyers, magazines, books, teaching materials, animations, video games and films. An illustration is typically created by an illustrator. Digital illustrations are often used to make websites and apps more user-friendly, such as the use of emojis to accompany digital type. llustration also means providing an example; either in writing or in picture form. The origin of the word "illustration" is late Middle English (in the sense ‘illumination; spiritual or intellectual enlightenment’): via Old French from Latin ''illustratio''(n-), from the verb ''illustrare''. Illustration styles Contemporary illustration uses a wide range of styles and techniques, including drawing, painting, printmaking, collage, Photomontage, montage, Interaction design, digital design, multimedia, 3D mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Frequency
In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier transform) of the structure repeat per unit of distance. The SI unit of spatial frequency is cycles per meter (m). In image-processing applications, spatial frequency is often expressed in units of cycles per millimeter (mm) or equivalently line pairs per mm. In wave propagation, the spatial frequency is also known as '' wavenumber''. Ordinary wavenumber is defined as the reciprocal of wavelength \lambda and is commonly denoted by \xi or sometimes \nu: :\xi = \frac. Angular wavenumber k, expressed in rad per m, is related to ordinary wavenumber and wavelength by :k = 2 \pi \xi = \frac. Visual perception In the study of visual perception, sinusoidal gratings are frequently used to probe the capabilities of the visual system. In these s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oversampling
In signal processing, oversampling is the process of sampling a signal at a sampling frequency significantly higher than the Nyquist rate. Theoretically, a bandwidth-limited signal can be perfectly reconstructed if sampled at the Nyquist rate or above it. The Nyquist rate is defined as twice the bandwidth of the signal. Oversampling is capable of improving resolution and signal-to-noise ratio, and can be helpful in avoiding aliasing and phase distortion by relaxing anti-aliasing filter performance requirements. A signal is said to be oversampled by a factor of ''N'' if it is sampled at ''N'' times the Nyquist rate. Motivation There are three main reasons for performing oversampling: to improve anti-aliasing performance, to increase resolution and to reduce noise. Anti-aliasing Oversampling can make it easier to realize analog anti-aliasing filters. Without oversampling, it is very difficult to implement filters with the sharp cutoff necessary to maximize use of the availab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency ( bandwidth) of a given function or signal. When the function is digitized at a higher sample rate (see ), the resulting discrete-time sequence is said to be free of the distortion known as aliasing. Conversely, for a given sample-rate the corresponding Nyquist frequency in Hz is one-half the sample-rate. Note that the ''Nyquist rate'' is a property of a continuous-time signal, whereas ''Nyquist frequency'' is a property of a discrete-time system. The term ''Nyquist rate'' is also used in a different context with units of symbols per second, which is actually the field in which Harry Nyquist was working. In that context it is an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line or passband channel such as a limited radio frequency band or a frequency division m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Resolution
Optical resolution describes the ability of an imaging system to resolve detail, in the object that is being imaged. An imaging system may have many individual components, including one or more lenses, and/or recording and display components. Each of these contributes (given suitable design, and adequate alignment) to the optical resolution of the system; the environment in which the imaging is done often is a further important factor. Lateral resolution Resolution depends on the distance between two distinguishable radiating points. The sections below describe the theoretical estimates of resolution, but the real values may differ. The results below are based on mathematical models of Airy discs, which assumes an adequate level of contrast. In low-contrast systems, the resolution may be much lower than predicted by the theory outlined below. Real optical systems are complex, and practical difficulties often increase the distance between distinguishable point sources. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zernike Polynomials
In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike, winner of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy, they play important roles in various optics branches such as beam optics and imaging. Definitions There are even and odd Zernike polynomials. The even Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\cos(m\,\varphi) \! (even function over the azimuthal angle \varphi), and the odd Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\sin(m\,\varphi), \! (odd function over the azimuthal angle \varphi) where ''m'' and ''n'' are nonnegative integers with ''n ≥ m ≥ 0'' (''m'' = 0 for even Zernike polynomials), ''\varphi'' is the azimuthal angle, ''ρ'' is the radial distance 0\le\rho\le 1, and R^m_n are the radial polynomials defined below. Zernike polynomials have the property of being l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Aberrations
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which is not sharp. Makers of optical instruments need to correct optical systems to compensate for aberration. Aberration can be ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trefoil Aberration PSF OTF And Example Image
A trefoil () is a graphic form composed of the outline of three overlapping rings, used in architecture and Christian symbolism, among other areas. The term is also applied to other symbols with a threefold shape. A similar shape with four rings is called a quatrefoil. Architecture Ornamentation 'Trefoil' is a term in Gothic architecture given to the ornamental foliation or cusping introduced in the heads of window-lights, tracery, and panellings, in which the centre takes the form of a three-lobed leaf (formed from three partially overlapping circles). One of the earliest examples is in the plate tracery at Winchester Cathedral (1222–1235). The fourfold version of an architectural trefoil is a quatrefoil. A simple trefoil shape in itself can be symbolic of the Trinity, while a trefoil combined with an equilateral triangle was also a moderately common symbol of the Christian Trinity during the late Middle Ages in some parts of Europe, similar to a barbed quatrefoil. Two fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aliasing
In signal processing and related disciplines, aliasing is an effect that causes different signals to become indistinguishable (or ''aliases'' of one another) when sampled. It also often refers to the distortion or artifact that results when a signal reconstructed from samples is different from the original continuous signal. Aliasing can occur in signals sampled in time, for instance digital audio, or the stroboscopic effect, and is referred to as temporal aliasing. It can also occur in spatially sampled signals (e.g. moiré patterns in digital images); this type of aliasing is called spatial aliasing. Aliasing is generally avoided by applying low-pass filters or anti-aliasing filters (AAF) to the input signal before sampling and when converting a signal from a higher to a lower sampling rate. Suitable reconstruction filtering should then be used when restoring the sampled signal to the continuous domain or converting a signal from a lower to a higher sampling rate. F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist–Shannon Sampling Theorem
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of ''samples'' to capture all the information from a continuous-time signal of finite bandwidth. Strictly speaking, the theorem only applies to a class of mathematical functions having a Fourier transform that is zero outside of a finite region of frequencies. Intuitively we expect that when one reduces a continuous function to a discrete sequence and interpolates back to a continuous function, the fidelity of the result depends on the density (or sample rate) of the original samples. The sampling theorem introduces the concept of a sample rate that is sufficient for perfect fidelity for the class of functions that are band-limited to a given bandwidth, such that no actual information is lost in the sampling proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-number
In optics, the f-number of an optical system such as a camera lens is the ratio of the system's focal length to the diameter of the entrance pupil ("clear aperture").Smith, Warren ''Modern Optical Engineering'', 4th Ed., 2007 McGraw-Hill Professional, p. 183. It is also known as the focal ratio, f-ratio, or f-stop, and is very important in photography. It is a dimensionless number that is a quantitative measure of lens speed; increasing the f-number is referred to as ''stopping down''. The f-number is commonly indicated using a lower-case hooked f with the format ''N'', where ''N'' is the f-number. The f-number is the reciprocal of the relative aperture (the aperture diameter divided by focal length). Notation The f-number is given by: N = \frac \ where f is the focal length, and D is the diameter of the entrance pupil (''effective aperture''). It is customary to write f-numbers preceded by "", which forms a mathematical expression of the entrance pupil diamet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Aberration
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which is not sharp. Makers of optical instruments need to correct optical systems to compensate for aberration. Aberration can be ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |