F-number on:
[Wikipedia]
[Google]
[Amazon]
 An f-number is a measure of the light-gathering ability of an optical system such as a
An f-number is a measure of the light-gathering ability of an optical system such as a

 Computing the f-number of the
Computing the f-number of the
 At the same time, there were a number of aperture numbering systems designed with the goal of making exposure times vary in direct or inverse proportion with the aperture, rather than with the square of the f-number or inverse square of the apertal ratio or intensity ratio. But these systems all involved some arbitrary constant, as opposed to the simple ratio of focal length and diameter.
For example, the ''Uniform System'' (U.S.) of apertures was adopted as a standard by the Photographic Society of Great Britain in the 1880s. Bothamley in 1891 said "The stops of all the best makers are now arranged according to this system." U.S. 16 is the same aperture as , but apertures that are larger or smaller by a full stop use doubling or halving of the U.S. number, for example is U.S. 8 and is U.S. 4. The exposure time required is directly proportional to the U.S. number.
At the same time, there were a number of aperture numbering systems designed with the goal of making exposure times vary in direct or inverse proportion with the aperture, rather than with the square of the f-number or inverse square of the apertal ratio or intensity ratio. But these systems all involved some arbitrary constant, as opposed to the simple ratio of focal length and diameter.
For example, the ''Uniform System'' (U.S.) of apertures was adopted as a standard by the Photographic Society of Great Britain in the 1880s. Bothamley in 1891 said "The stops of all the best makers are now arranged according to this system." U.S. 16 is the same aperture as , but apertures that are larger or smaller by a full stop use doubling or halving of the U.S. number, for example is U.S. 8 and is U.S. 4. The exposure time required is directly proportional to the U.S. number. 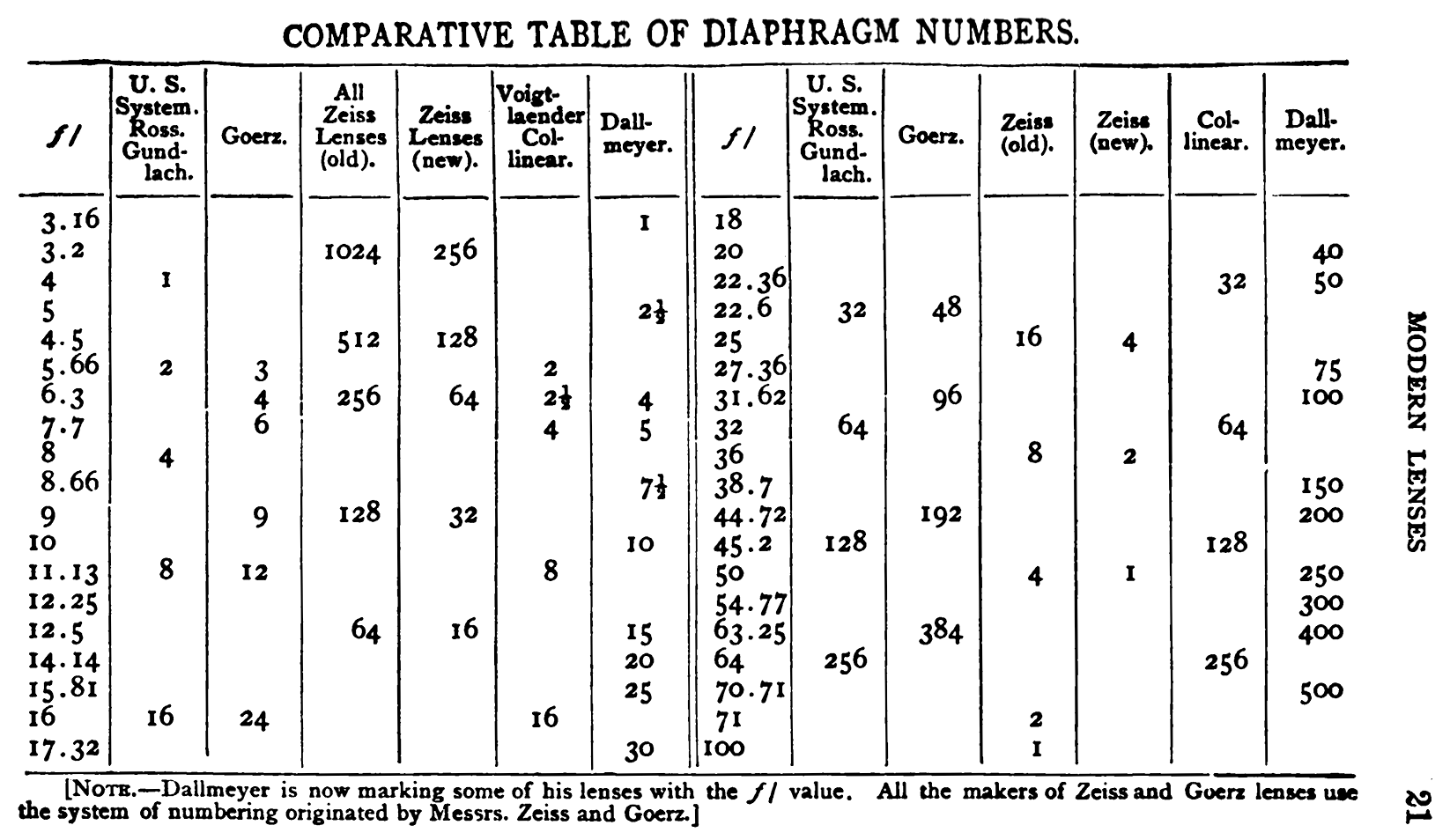 Piper in 1901 discusses five different systems of aperture marking: the old and new Zeiss systems based on actual intensity (proportional to reciprocal square of the f-number); and the U.S., C.I., and Dallmeyer systems based on exposure (proportional to square of the f-number). He calls the f-number the "ratio number", "aperture ratio number", and "ratio aperture". He calls expressions like the "fractional diameter" of the aperture, even though it is literally equal to the "absolute diameter" which he distinguishes as a different term. He also sometimes uses expressions like "an aperture of f 8" without the division indicated by the slash.
Beck and Andrews in 1902 talk about the Royal Photographic Society standard of , , , , etc. The R.P.S. had changed their name and moved off of the U.S. system some time between 1895 and 1902.
Piper in 1901 discusses five different systems of aperture marking: the old and new Zeiss systems based on actual intensity (proportional to reciprocal square of the f-number); and the U.S., C.I., and Dallmeyer systems based on exposure (proportional to square of the f-number). He calls the f-number the "ratio number", "aperture ratio number", and "ratio aperture". He calls expressions like the "fractional diameter" of the aperture, even though it is literally equal to the "absolute diameter" which he distinguishes as a different term. He also sometimes uses expressions like "an aperture of f 8" without the division indicated by the slash.
Beck and Andrews in 1902 talk about the Royal Photographic Society standard of , , , , etc. The R.P.S. had changed their name and moved off of the U.S. system some time between 1895 and 1902.

 By 1920, the term ''f-number'' appeared in books both as ''F number'' and ''f/number''. In modern publications, the forms ''f-number'' and ''f number'' are more common, though the earlier forms, as well as ''F-number'' are still found in a few books; not uncommonly, the initial lower-case ''f'' in ''f-number'' or ''f/number'' is set in a hooked italic form: Æ’.
Notations for f-numbers were also quite variable in the early part of the twentieth century. They were sometimes written with a capital F, sometimes with a dot (period) instead of a slash, and sometimes set as a vertical fraction.
The 1961 ASA standard PH2.12-1961 ''American Standard General-Purpose Photographic Exposure Meters (Photoelectric Type)'' specifies that "The symbol for relative apertures shall be or followed by the effective Æ’-number." They show the hooked italic 'Æ’' not only in the symbol, but also in the term ''f-number'', which today is more commonly set in an ordinary non-italic face.
By 1920, the term ''f-number'' appeared in books both as ''F number'' and ''f/number''. In modern publications, the forms ''f-number'' and ''f number'' are more common, though the earlier forms, as well as ''F-number'' are still found in a few books; not uncommonly, the initial lower-case ''f'' in ''f-number'' or ''f/number'' is set in a hooked italic form: Æ’.
Notations for f-numbers were also quite variable in the early part of the twentieth century. They were sometimes written with a capital F, sometimes with a dot (period) instead of a slash, and sometimes set as a vertical fraction.
The 1961 ASA standard PH2.12-1961 ''American Standard General-Purpose Photographic Exposure Meters (Photoelectric Type)'' specifies that "The symbol for relative apertures shall be or followed by the effective Æ’-number." They show the hooked italic 'Æ’' not only in the symbol, but also in the term ''f-number'', which today is more commonly set in an ordinary non-italic face.
Large format photography—how to select the f-stop
{{photography Optical quantities Science of photography Dimensionless numbers of physics Logarithmic scales of measurement
camera lens
A camera lens, photographic lens or photographic objective is an optical lens (optics), lens or assembly of lenses (compound lens) used in conjunction with a camera body and mechanism to Imaging, make images of objects either on photographic film ...
. It is calculated by dividing the system's focal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
by the diameter of the entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the optical elements in front of the stop. The corresponding image of the aperture stop as seen through the optical elements behin ...
("clear aperture
In optics, the aperture of an optical system (including a system consisting of a single lens) is the hole or opening that primarily limits light propagated through the system. More specifically, the entrance pupil as the front side image o ...
").Smith, Warren ''Modern Optical Engineering'', 4th Ed., 2007 McGraw-Hill Professional, p. 183. The f-number is also known as the focal ratio, f-ratio, or f-stop, and it is key in determining the depth of field
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus (optics), focus in an image captured with a camera. See also the closely related depth of focus.
Factors affecting depth ...
, diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
, and exposure of a photograph. The f-number is dimensionless
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another sy ...
and is usually expressed using a lower-case hooked f with the format ''N'', where ''N'' is the f-number.
The f-number is also known as the inverse relative aperture, because it is the inverse of the relative aperture, defined as the aperture diameter divided by focal length. The relative aperture indicates how much light can pass through the lens at a given focal length. A lower f-number means a larger relative aperture and more light entering the system, while a higher f-number means a smaller relative aperture and less light entering the system. The f-number is related to the numerical aperture
In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, has the property ...
(NA) of the system, which measures the range of angles over which light can enter or exit the system. The numerical aperture takes into account the refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
of the medium in which the system is working, while the f-number does not.
Notation
The f-number is given by: where is thefocal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
, and is the diameter of the entrance pupil (''effective aperture''). It is customary to write f-numbers preceded by "", which forms a mathematical expression of the entrance pupil's diameter in terms of and . For example, if a lens's focal length were and its entrance pupil's diameter were , the f-number would be 2. This would be expressed as in a lens system. The aperture diameter would be equal to .
Camera lenses often include an adjustable diaphragm, which changes the size of the aperture stop
In optics, the aperture of an optical system (including a system consisting of a single lens) is the hole or opening that primarily limits light propagated through the system. More specifically, the entrance pupil as the front side image of ...
and thus the entrance pupil size. This allows the user to vary the f-number as needed. The entrance pupil diameter is not necessarily equal to the aperture stop diameter, because of the magnifying effect of lens elements in front of the aperture.
Ignoring differences in light transmission efficiency, a lens with a greater f-number projects darker images. The brightness of the projected image (illuminance
In photometry (optics), photometry, illuminance is the total luminous flux incident on a surface, per unit area. It is a measure of how much the incident light illuminates the surface, wavelength-weighted by the luminosity function to correlate ...
) relative to the brightness of the scene in the lens's field of view (luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls wit ...
) decreases with the square of the f-number. A focal length lens has an entrance pupil diameter of . A focal length lens has an entrance pupil diameter of . Since the area is proportional to the square of the pupil diameter, the amount of light admitted by the lens is four times that of the lens. To obtain the same photographic exposure, the exposure time must be reduced by a factor of four.
A focal length lens has an entrance pupil diameter of . The lens's entrance pupil has four times the area of the lens's entrance pupil, and thus collects four times as much light from each object in the lens's field of view. But compared to the lens, the lens projects an image of each object twice as high and twice as wide, covering four times the area, and so both lenses produce the same illuminance at the focal plane when imaging a scene of a given luminance.
Stops, f-stop conventions, and exposure
The word ''stop'' is sometimes confusing due to its multiple meanings. A stop can be a physical object: an opaque part of an optical system that blocks certain rays. The ''aperture stop
In optics, the aperture of an optical system (including a system consisting of a single lens) is the hole or opening that primarily limits light propagated through the system. More specifically, the entrance pupil as the front side image of ...
'' is the aperture setting that limits the brightness of the image by restricting the input pupil size, while a ''field stop'' is a stop intended to cut out light that would be outside the desired field of view and might cause flare or other problems if not stopped.
In photography, stops are also a ''unit'' used to quantify ratios of light or exposure, with each added stop meaning a factor of two, and each subtracted stop meaning a factor of one-half. The one-stop unit is also known as the EV (exposure value
In photography, exposure value (EV) is a number that represents a combination of a camera's shutter speed and f-number, such that all combinations that yield the same exposure (photography), exposure have the same EV (for any fixed scene luminanc ...
) unit. On a camera, the aperture setting is traditionally adjusted in discrete steps, known as ''f-stops''. Each "stop" is marked with its corresponding f-number, and represents a halving of the light intensity from the previous stop. This corresponds to a decrease of the pupil and aperture diameters by a factor of 1/ or about 0.7071, and hence a halving of the area of the pupil.
Most modern lenses use a standard f-stop scale, which is an approximately geometric sequence of numbers that corresponds to the sequence of the powers of the square root of 2
The square root of 2 (approximately 1.4142) is the positive real number that, when multiplied by itself or squared, equals the number 2. It may be written as \sqrt or 2^. It is an algebraic number, and therefore not a transcendental number. Te ...
: , , , , , , , , , , , , , , , etc. Each element in the sequence is one stop lower than the element to its left, and one stop higher than the element to its right. The values of the ratios are rounded off to these particular conventional numbers, to make them easier to remember and write down.
The sequence above is obtained by approximating the following exact geometric sequence:
In the same way as one f-stop corresponds to a factor of two in light intensity, shutter speed
In photography, shutter speed or exposure time is the length of time that the film or digital sensor inside the camera is exposed to light (that is, when the camera's shutter (photography), shutter is open) when taking a photograph.
The am ...
s are arranged so that each setting differs in duration by a factor of approximately two from its neighbour. Opening up a lens by one stop allows twice as much light to fall on the film in a given period of time. Therefore, to have the same exposure at this larger aperture as at the previous aperture, the shutter would be opened for half as long (i.e., twice the speed). The film will respond equally to these equal amounts of light, since it has the property of '' reciprocity''. This is less true for extremely long or short exposures, where there is reciprocity failure. Aperture, shutter speed, and film sensitivity are linked: for constant scene brightness, doubling the aperture area (one stop), halving the shutter speed (doubling the time open), or using a film twice as sensitive, has the same effect on the exposed image. For all practical purposes extreme accuracy is not required (mechanical shutter speeds were notoriously inaccurate as wear and lubrication varied, with no effect on exposure). It is not significant that aperture areas and shutter speeds do not vary by a factor of precisely two.
Photographers sometimes express other exposure ratios in terms of 'stops'. Ignoring the f-number markings, the f-stops make a logarithmic scale
A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved.
Unlike a linear Scale (measurement) ...
of exposure intensity. Given this interpretation, one can then think of taking a half-step along this scale, to make an exposure difference of a "half stop".
Fractional stops
Most twentieth-century cameras had a continuously variable aperture, using an iris diaphragm, with each full stop marked. Click-stopped aperture came into common use in the 1960s; the aperture scale usually had a click stop at every whole and half stop. On modern cameras, especially when aperture is set on the camera body, f-number is often divided more finely than steps of one stop. Steps of one-third stop ( EV) are the most common, since this matches the ISO system offilm speed
Film speed is the measure of a photographic film's sensitivity to light, determined by sensitometry and measured on various numerical scales, the most recent being the ISO system introduced in 1974. A closely related system, also known as IS ...
s. Half-stop steps are used on some cameras. Usually the full stops are marked, and the intermediate positions click but are not marked. As an example, the aperture that is one-third stop smaller than is , two-thirds smaller is , and one whole stop smaller is . The next few f-stops in this sequence are:
To calculate the steps in a full stop (1 EV) one could use
The steps in a half stop ( EV) series would be
The steps in a third stop ( EV) series would be
As in the earlier DIN and ASA film-speed standards, the ISO speed is defined only in one-third stop increments, and shutter speeds of digital cameras are commonly on the same scale in reciprocal seconds. A portion of the ISO range is the sequence
while shutter speeds in reciprocal seconds have a few conventional differences in their numbers (, , and second instead of , , and ).
In practice the maximum aperture of a lens is often not an integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
power of (i.e., to the power of a whole number), in which case it is usually a half or third stop above or below an integral power of .
Modern electronically controlled interchangeable lenses, such as those used for SLR cameras, have f-stops specified internally in -stop increments, so the cameras' -stop settings are approximated by the nearest -stop setting in the lens.
Standard full-stop f-number scale
Including aperture value AV: Conventional and calculated f-numbers, full-stop series:Typical one-half-stop f-number scale
Typical one-third-stop f-number scale
Sometimes the same number is included on several scales; for example, an aperture of may be used in either a half-stop or a one-third-stop system; sometimes and and other differences are used for the one-third stop scale.Typical one-quarter-stop f-number scale
H-stop
An H-stop (for hole, by convention written with capital letter H) is an f-number equivalent for effective exposure based on the area covered by the holes in the diffusion discs or sieve aperture found in Rodenstock Imagon lenses.T-stop
A T-stop (for transmission stops, by convention written with capital letter T) is an f-number adjusted to account for light transmission efficiency (''transmittance
Electromagnetic radiation can be affected in several ways by the medium in which it propagates. It can be Scattering, scattered, Absorption (electromagnetic radiation), absorbed, and Fresnel equations, reflected and refracted at discontinui ...
''). A lens with a T-stop of projects an image of the same brightness as an ideal lens with 100% transmittance and an f-number of . A particular lens's T-stop, , is given by dividing the f-number by the square root of the transmittance of that lens:
For example, an lens with transmittance of 75% has a T-stop of 2.3:
Since real lenses have transmittances of less than 100%, a lens's T-stop number is always greater than its f-number.
With 8% loss per air-glass surface on lenses without coating, multicoating of lenses is the key in lens design to decrease transmittance losses of lenses. Some reviews of lenses do measure the T-stop or transmission rate in their benchmarks. T-stops are sometimes used instead of f-numbers to more accurately determine exposure, particularly when using external light meter
A light meter (or illuminometer) is a device used to measure the amount of light. In photography, an exposure meter is a light meter coupled to either a Digital data, digital or analog calculator which displays the correct shutter speed and f-nu ...
s. Lens transmittances of 60%–95% are typical. T-stops are often used in cinematography, where many images are seen in rapid succession and even small changes in exposure will be noticeable. Cinema camera lenses are typically calibrated in T-stops instead of f-numbers. In still photography, without the need for rigorous consistency of all lenses and cameras used, slight differences in exposure are less important; however, T-stops are still used in some kinds of special-purpose lenses such as Smooth Trans Focus lenses by Minolta
was a Japanese manufacturer of cameras, lenses, camera accessories, photocopiers, fax machines, and laser printers. Minolta Co., Ltd., which is also known simply as Minolta, was founded in Osaka, Japan, in 1928 as . It made the first integrated ...
and Sony
is a Japanese multinational conglomerate (company), conglomerate headquartered at Sony City in Minato, Tokyo, Japan. The Sony Group encompasses various businesses, including Sony Corporation (electronics), Sony Semiconductor Solutions (i ...
.
ASA/ISO numbers
Photographic film
Photographic film is a strip or sheet of transparent film base coated on one side with a gelatin photographic emulsion, emulsion containing microscopically small light-sensitive silver halide crystals. The sizes and other characteristics of the ...
's and electronic camera sensor's sensitivity to light is often specified using ASA/ISO numbers. Both systems have a linear number where a doubling of sensitivity is represented by a doubling of the number, and a logarithmic number. In the ISO system, a 3° increase in the logarithmic number corresponds approximately to a doubling of sensitivity. Doubling or halving the sensitivity is equal to a difference of one T-stop in terms of light transmittance.
Gain
Most electronic cameras allow the user to adjust the amplification of the signal coming from the image sensor. This amplification is usually called gain and is measured in decibels. A of gain is roughly equivalent to one T-stop in terms of light transmittance. Many camcorders have a unified control over the lens f-number and gain. In this case, starting from (arbitrarily defined) zero gain and a fully open iris, one can either increase the f-number by reducing the iris size while gain remains zero, or increase the gain while the iris remains fully open.Sunny 16 rule
An example of the use of f-numbers in photography is the '' sunny 16 rule'': an approximately correct exposure will be obtained on a sunny day by using an aperture of and the shutter speed closest to the reciprocal of the ISO speed of the film; for example, using ISO 200 film, an aperture of and a shutter speed of second. The f-number may then be adjusted downwards for situations with lower light. Selecting a lower f-number is "opening up" the lens. Selecting a higher f-number is "closing" or "stopping down" the lens.Effects on image sharpness

Depth of field
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus (optics), focus in an image captured with a camera. See also the closely related depth of focus.
Factors affecting depth ...
increases with f-number, as illustrated in the image here. This means that photographs taken with a low f-number (large aperture) will tend to have subjects at one distance in focus, with the rest of the image (nearer and farther elements) out of focus. This is frequently used for nature photography
Nature photography encompasses a wide range of photography taken outdoors and devoted to displaying natural elements such as landscapes, wildlife, plants, and close-ups of natural scenes and textures. Nature photography tends to place a stronger ...
and portraiture because background blur (the aesthetic quality known as ' bokeh') can be aesthetically pleasing and puts the viewer's focus on the main subject in the foreground. The depth of field
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus (optics), focus in an image captured with a camera. See also the closely related depth of focus.
Factors affecting depth ...
of an image produced at a given f-number is dependent on other parameters as well, including the focal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
, the subject distance, and the format of the film or sensor used to capture the image. Depth of field can be described as depending on just angle of view, subject distance, and entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the optical elements in front of the stop. The corresponding image of the aperture stop as seen through the optical elements behin ...
diameter (as in von Rohr's method). As a result, smaller formats will have a deeper field than larger formats at the same f-number for the same distance of focus and same angle of view
In photography, angle of view (AOV) describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term '' field of view''.
It is important to distinguish the angle of view from the ...
since a smaller format requires a shorter focal length (wider angle lens) to produce the same angle of view, and depth of field increases with shorter focal lengths. Therefore, reduced–depth-of-field effects will require smaller f-numbers (and thus potentially more difficult or complex optics) when using small-format cameras than when using larger-format cameras.
Beyond focus, image sharpness is related to f-number through two different optical effects: aberration, due to imperfect lens design, and diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
which is due to the wave nature of light. The blur-optimal f-stop varies with the lens design. For modern standard lenses having six or seven elements, the sharpest image is often obtained around –, while for older standard lenses having only four elements ( Tessar formula) stopping to will give the sharpest image. The larger number of elements in modern lenses allow the designer to compensate for aberrations, allowing the lens to give better pictures at lower f-numbers. At small apertures, depth of field and aberrations are improved, but diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
creates more spreading of the light, causing blur.
Light falloff is also sensitive to f-stop. Many wide-angle lenses will show a significant light falloff (vignetting
In photography and optics, vignetting ( ) is a reduction of an image's brightness or saturation toward the periphery compared to the image center. The word '' vignette'', from the same root as ''vine'', originally referred to a decorative b ...
) at the edges for large apertures.
Photojournalist
Photojournalism is journalism that uses images to tell a news story. It usually only refers to still images, but can also refer to video used in broadcast journalism. Photojournalism is distinguished from other close branches of photography (suc ...
s have a saying, " and be there", meaning that being on the scene is more important than worrying about technical details. Practically, (in 35 mm and larger formats) allows adequate depth of field and sufficient lens speed for a decent base exposure in most daylight situations.
Human eye
 Computing the f-number of the
Computing the f-number of the human eye
The human eye is a sensory organ in the visual system that reacts to light, visible light allowing eyesight. Other functions include maintaining the circadian rhythm, and Balance (ability), keeping balance.
The eye can be considered as a living ...
involves computing the physical aperture and focal length of the eye. Typically, the pupil can dilate to be as large as 6–7 mm in darkness, which translates into the maximal physical aperture. Some individuals' pupils can dilate to over 9 mm wide.
The f-number of the human eye varies from about in a very brightly lit place to about in the dark. Computing the focal length requires that the light-refracting properties of the liquids in the eye be taken into account. Treating the eye as an ordinary air-filled camera and lens results in an incorrect focal length and f-number.
Focal ratio in telescopes
In astronomy, the f-number is commonly referred to as the ''focal ratio'' (or ''f-ratio'') notated as . It is still defined as thefocal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
of an objective divided by its diameter or by the diameter of an aperture
In optics, the aperture of an optical system (including a system consisting of a single lens) is the hole or opening that primarily limits light propagated through the system. More specifically, the entrance pupil as the front side image o ...
stop in the system:
Even though the principles of focal ratio are always the same, the application to which the principle is put can differ. In photography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
the focal ratio varies the focal-plane illuminance (or optical power per unit area in the image) and is used to control variables such as depth of field
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus (optics), focus in an image captured with a camera. See also the closely related depth of focus.
Factors affecting depth ...
. When using an optical telescope
An optical telescope gathers and focus (optics), focuses light mainly from the visible spectrum, visible part of the electromagnetic spectrum, to create a magnification, magnified image for direct visual inspection, to make a photograph, or to co ...
in astronomy, there is no depth of field issue, and the brightness of stellar point sources in terms of total optical power (not divided by area) is a function of absolute aperture area only, independent of focal length. The focal length controls the field of view
The field of view (FOV) is the angle, angular extent of the observable world that is visual perception, seen at any given moment. In the case of optical instruments or sensors, it is a solid angle through which a detector is sensitive to elec ...
of the instrument and the scale of the image that is presented at the focal plane to an eyepiece
An eyepiece, or ocular lens, is a type of lens that is attached to a variety of optical devices such as Optical telescope, telescopes and microscopes. It is named because it is usually the lens that is closest to the eye when someone looks thro ...
, film plate, or CCD.
For example, the SOAR four-meter telescope has a small field of view (about ) which is useful for stellar studies. The LSST 8.4 m telescope, which will cover the entire sky every three days, has a very large field of view. Its short 10.3 m focal length () is made possible by an error correction system which includes secondary and tertiary mirrors, a three element refractive system and active mounting and optics.
Camera equation (G#)
The camera equation, or G#, is the ratio of theradiance
In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiati ...
reaching the camera sensor to the irradiance on the focal plane of the camera lens
A camera lens, photographic lens or photographic objective is an optical lens (optics), lens or assembly of lenses (compound lens) used in conjunction with a camera body and mechanism to Imaging, make images of objects either on photographic film ...
:
where is the transmission coefficient of the lens, and the units are in inverse steradian
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the fo ...
s (sr−1).
Working f-number
The f-number accurately describes the light-gathering ability of a lens only for objects an infinite distance away. p. 29. This limitation is typically ignored in photography, where f-number is often used regardless of the distance to the object. In optical design, an alternative is often needed for systems where the object is not far from the lens. In these cases the working f-number is used. The working f-number is given by: where is the uncorrected f-number, is the image-spacenumerical aperture
In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, has the property ...
of the lens, is the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of the lens's magnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, so ...
for an object a particular distance away, and is the pupil magnification. Since the pupil magnification is seldom known it is often assumed to be 1, which is the correct value for all symmetric lenses.
In photography this means that as one focuses closer, the lens's effective aperture becomes smaller, making the exposure darker. The working f-number is often described in photography as the f-number corrected for lens extensions by a bellows factor. This is of particular importance in macro photography.
History
The system of f-numbers for specifying relative apertures evolved in the late nineteenth century, in competition with several other systems of aperture notation.Origins of relative aperture
In 1867, Sutton and Dawson defined "apertal ratio" as essentially the reciprocal of the modern f-number. In the following quote, an "apertal ratio" of "" is calculated as the ratio of to , corresponding to an f-stop:In every lens there is, corresponding to a given apertal ratio (that is, the ratio of the diameter of the stop to the focal length), a certain distance of a near object from it, between which and infinity all objects are in equally good focus. For instance, in a single view lens of 6-inch focus, with a in. stop (apertal ratio one-twenty-fourth), all objects situated at distances lying between 20 feet from the lens and an infinite distance from it (a fixed star, for instance) are in equally good focus. Twenty feet is therefore called the 'focal range' of the lens when this stop is used. The focal range is consequently the distance of the nearest object, which will be in good focus when the ground glass is adjusted for an extremely distant object. In the same lens, the focal range will depend upon the size of the diaphragm used, while in different lenses having the same apertal ratio the focal ranges will be greater as the focal length of the lens is increased. The terms 'apertal ratio' and 'focal range' have not come into general use, but it is very desirable that they should, in order to prevent ambiguity and circumlocution when treating of the properties of photographic lenses.Thomas Sutton and George Dawson, ''A Dictionary of Photography'', London: Sampson Low, Son & Marston, 1867, (p. 122).In 1874, John Henry Dallmeyer called the ratio the "intensity ratio" of a lens:
The ''rapidity'' of a lens depends upon the relation or ratio of the aperture to the equivalent focus. To ascertain this, divide the ''equivalent focus'' by the diameter of the actual ''working aperture'' of the lens in question; and note down the quotient as the denominator with 1, or unity, for the numerator. Thus to find the ratio of a lens of 2 inches diameter and 6 inches focus, divide the focus by the aperture, or 6 divided by 2 equals 3; i.e., is the intensity ratio.John Henry Dallmeyer, ''Photographic Lenses: On Their Choice and Use – Special Edition Edited for American Photographers'', pamphlet, 1874.Although he did not yet have access to Ernst Abbe's theory of stops and pupils, which was made widely available by Siegfried Czapski in 1893,Siegfried Czapski, ''Theorie der optischen Instrumente, nach Abbe,'' Breslau: Trewendt, 1893. Dallmeyer knew that his ''working aperture'' was not the same as the physical diameter of the aperture stop:
It must be observed, however, that in order to find the real ''intensity ratio'', the diameter of the actual working aperture must be ascertained. This is easily accomplished in the case of single lenses, or for double combination lenses used with the full opening, these merely requiring the application of a pair of compasses or rule; but when double or triple-combination lenses are used, with stops inserted ''between'' the combinations, it is somewhat more troublesome; for it is obvious that in this case the diameter of the stop employed is not the measure of the actual pencil of light transmitted by the front combination. To ascertain this, focus for a distant object, remove the focusing screen and replace it by the collodion slide, having previously inserted a piece of cardboard in place of the prepared plate. Make a small round hole in the centre of the cardboard with a piercer, and now remove to a darkened room; apply a candle close to the hole, and observe the illuminated patch visible upon the front combination; the diameter of this circle, carefully measured, is the actual working aperture of the lens in question for the particular stop employed.This point is further emphasized by Czapski in 1893. According to an English review of his book, in 1894, "The necessity of clearly distinguishing between effective aperture and diameter of physical stop is strongly insisted upon." J. H. Dallmeyer's son, Thomas Rudolphus Dallmeyer, inventor of the telephoto lens, followed the ''intensity ratio'' terminology in 1899.
Aperture numbering systems
 At the same time, there were a number of aperture numbering systems designed with the goal of making exposure times vary in direct or inverse proportion with the aperture, rather than with the square of the f-number or inverse square of the apertal ratio or intensity ratio. But these systems all involved some arbitrary constant, as opposed to the simple ratio of focal length and diameter.
For example, the ''Uniform System'' (U.S.) of apertures was adopted as a standard by the Photographic Society of Great Britain in the 1880s. Bothamley in 1891 said "The stops of all the best makers are now arranged according to this system." U.S. 16 is the same aperture as , but apertures that are larger or smaller by a full stop use doubling or halving of the U.S. number, for example is U.S. 8 and is U.S. 4. The exposure time required is directly proportional to the U.S. number.
At the same time, there were a number of aperture numbering systems designed with the goal of making exposure times vary in direct or inverse proportion with the aperture, rather than with the square of the f-number or inverse square of the apertal ratio or intensity ratio. But these systems all involved some arbitrary constant, as opposed to the simple ratio of focal length and diameter.
For example, the ''Uniform System'' (U.S.) of apertures was adopted as a standard by the Photographic Society of Great Britain in the 1880s. Bothamley in 1891 said "The stops of all the best makers are now arranged according to this system." U.S. 16 is the same aperture as , but apertures that are larger or smaller by a full stop use doubling or halving of the U.S. number, for example is U.S. 8 and is U.S. 4. The exposure time required is directly proportional to the U.S. number. Eastman Kodak
The Eastman Kodak Company, referred to simply as Kodak (), is an American public company that produces various products related to its historic basis in film photography. The company is headquartered in Rochester, New York, and is incorporated i ...
used U.S. stops on many of their cameras at least in the 1920s.
By 1895, Hodges contradicts Bothamley, saying that the f-number system has taken over: "This is called the system, and the diaphragms of all modern lenses of good construction are so marked."
Here is the situation as seen in 1899:
 Piper in 1901 discusses five different systems of aperture marking: the old and new Zeiss systems based on actual intensity (proportional to reciprocal square of the f-number); and the U.S., C.I., and Dallmeyer systems based on exposure (proportional to square of the f-number). He calls the f-number the "ratio number", "aperture ratio number", and "ratio aperture". He calls expressions like the "fractional diameter" of the aperture, even though it is literally equal to the "absolute diameter" which he distinguishes as a different term. He also sometimes uses expressions like "an aperture of f 8" without the division indicated by the slash.
Beck and Andrews in 1902 talk about the Royal Photographic Society standard of , , , , etc. The R.P.S. had changed their name and moved off of the U.S. system some time between 1895 and 1902.
Piper in 1901 discusses five different systems of aperture marking: the old and new Zeiss systems based on actual intensity (proportional to reciprocal square of the f-number); and the U.S., C.I., and Dallmeyer systems based on exposure (proportional to square of the f-number). He calls the f-number the "ratio number", "aperture ratio number", and "ratio aperture". He calls expressions like the "fractional diameter" of the aperture, even though it is literally equal to the "absolute diameter" which he distinguishes as a different term. He also sometimes uses expressions like "an aperture of f 8" without the division indicated by the slash.
Beck and Andrews in 1902 talk about the Royal Photographic Society standard of , , , , etc. The R.P.S. had changed their name and moved off of the U.S. system some time between 1895 and 1902.
Typographical standardization

 By 1920, the term ''f-number'' appeared in books both as ''F number'' and ''f/number''. In modern publications, the forms ''f-number'' and ''f number'' are more common, though the earlier forms, as well as ''F-number'' are still found in a few books; not uncommonly, the initial lower-case ''f'' in ''f-number'' or ''f/number'' is set in a hooked italic form: Æ’.
Notations for f-numbers were also quite variable in the early part of the twentieth century. They were sometimes written with a capital F, sometimes with a dot (period) instead of a slash, and sometimes set as a vertical fraction.
The 1961 ASA standard PH2.12-1961 ''American Standard General-Purpose Photographic Exposure Meters (Photoelectric Type)'' specifies that "The symbol for relative apertures shall be or followed by the effective Æ’-number." They show the hooked italic 'Æ’' not only in the symbol, but also in the term ''f-number'', which today is more commonly set in an ordinary non-italic face.
By 1920, the term ''f-number'' appeared in books both as ''F number'' and ''f/number''. In modern publications, the forms ''f-number'' and ''f number'' are more common, though the earlier forms, as well as ''F-number'' are still found in a few books; not uncommonly, the initial lower-case ''f'' in ''f-number'' or ''f/number'' is set in a hooked italic form: Æ’.
Notations for f-numbers were also quite variable in the early part of the twentieth century. They were sometimes written with a capital F, sometimes with a dot (period) instead of a slash, and sometimes set as a vertical fraction.
The 1961 ASA standard PH2.12-1961 ''American Standard General-Purpose Photographic Exposure Meters (Photoelectric Type)'' specifies that "The symbol for relative apertures shall be or followed by the effective Æ’-number." They show the hooked italic 'Æ’' not only in the symbol, but also in the term ''f-number'', which today is more commonly set in an ordinary non-italic face.
See also
* Circle of confusion * Group f/64 * Photographic lens design *Pinhole camera
A pinhole camera is a simple camera without a lens but with a tiny aperture (the so-called ''Pinhole (optics), pinhole'')—effectively a light-proof box with a small hole in one side. Light from a scene passes through the aperture and projects a ...
* Preferred number
References
External links
Large format photography—how to select the f-stop
{{photography Optical quantities Science of photography Dimensionless numbers of physics Logarithmic scales of measurement