|
P-FEM
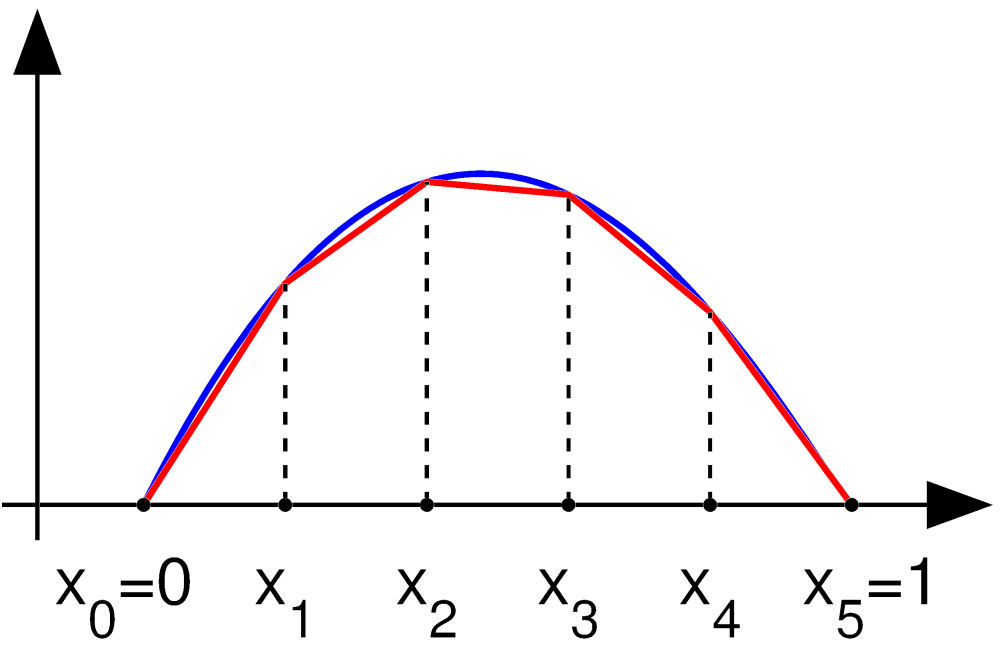
p-FEM or the p-version of the finite element method is a numerical method for solving partial differential equations. It is a discretization strategy in which the finite element mesh is fixed and the polynomial degrees of elements are increased such that the lowest polynomial degree, denoted by p_, approaches infinity. This is in contrast with the "h-version" or "h-FEM", a widely used discretization strategy, in which the polynomial degrees of elements are fixed and the mesh is refined such that the diameter of the largest element, denoted by h_ approaches zero. It was demonstrated on the basis of a linear elastic fracture mechanics problem that sequences of finite element solutions based on the p-version converge faster than sequences based on the h-version by Szabó and Mehta in 1978. The theoretical foundations of the p-version were established in a paper published Babuška, Szabó and Katz in 1981 where it was shown that for a large class of problems the asymptotic rate of con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barna Szabó
Barna A. Szabó (born September 21, 1935) is a Hungarian-American engineer and educator, noted for his contributions on the finite element method, particularly the conception and implementation of the p- and hp-versions of the Finite Element Method. He is a founding member and fellow of the United States Association for Computational Mechanics, an external member of the Hungarian Academy of Sciences and fellow of the St. Louis Academy of Sciences. Life Barna Aladár Szabó was born in Martonvásár, Hungary, the son of József and Gizella (Iványi) Szabó. After graduating from the Franciscan High School in Esztergom in 1954, he was admitted to the Faculty of Mining Engineering of the Technical University of Heavy Industry in Miskolc (now University of Miskolc). Following the failed Hungarian uprising in 1956 he emigrated to Canada, where he resumed his undergraduate studies at the University of Toronto, receiving his Bachelor of Science in 1960. In 1963 he began part-time st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mehta A
Mehta is an Indian surname, derived from the Sanskrit word ''mahita'' meaning 'great' or 'praised'. It is found among several Indian religious groups, including Hindus, Sikhs, Jains and Parsis. Among Hindus, it is used by a wide range of castes and social groups, including Brahmins, Rajputs and Khatri (caste). Among Oswals, Porwal, and Punjabi Khatris, Mehta is a clan name.Dictionary of American Family Names Oxford University Press, Notable people Notable individuals with this surname include: * Aditya Mehta (born 1985), snooker player *[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ivo Babuska
Ivo is a masculine given name, in use in various European languages. The name used in western European languages originates as a Normannic name recorded since the High Middle Ages, and the French name Yves is a variant of it. The unrelated South Slavic name is a variant of the name Ivan (John). Origins The name is recorded from the High Middle Ages among the Normans of France and England ( Yvo of Chartres, born c. 1040). The name's etymology may be either Germanic or Celtic, in either case deriving from a given name with a first element meaning "yew" (Gaulish ''Ivo-'', Germanic ''Iwa-'').Campbell, MikIvo(Behind the Name: The Etymology and History of First Names) The name may have been spread by the cult of Saint Ivo (d. 1303), patron saint of Brittany. The Slavic name is a hypocorism, like its variant '' Ivica''. Variations Ivo has the genitive form of "Ives" in the place name St Ives. In France, the usual variation of the name is Yves. In the Hispanic countries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |